概率论与数理统计学习:随机向量(三)——知识总结与C语言实现案例
hello,大家好
这里是第八期概率论与数理统计的学习,我将用这篇博客去总结这期的知识点以及实现用C语言去做题的过程。

本期知识点:
- 条件分布
- 条件分布的概念
- 离散型随机变量的条件概率分布
- 连续型随机变量的条件概率密度
- 随机变量的独立性
条件分布
☁️ 条件分布的概念
请大家先回忆一下,我们最开始是不是也学过这个啥条件的东西?
对的,在前面的那叫条件概率,是对随机事件而言的,因为那时还没引入随机变量。(在这里呢大家可以看看前面那期有关条件概率的博客 → \rightarrow →条件概率)
注意了嗷,但这个知识点的标题是条件分布,其实两者概念上是差不多的,只是针对的知识点不同而已。
那么什么是条件分布呢?“分布”一词是与随机变量绑定在一起的,所以,也就是说条件分布一定是与随机变量有关的。
定义:设有两个随机变量 X X X和 Y Y Y,在给定了 Y Y Y取某个值或某些值的条件下, X X X的分布称为 X X X的条件分布。同时也要注意❗️,这两个随机变量是有联系的,即它们之间可以构成随机向量的关系。
既然概念已经搞清楚了,又因为它还是涉及到随机变量,而我们所学习的随机变量又分为两种情况:离散型和连续型。所以下面又是对这两种情况分别讲解。
![]()
☁️ 离散型随机变量的条件概率分布
首先,我们需要借鉴一下下条件概率的知识点。对于两个事件 A A A和 B B B,我们知道在 B B B已发生的条件下 A A A发生的概率的求法为: P ( A ∣ B ) = P ( A B ) P ( B ) P(A|B)=\frac{P(AB)}{P(B)} P(A∣B)=P(B)P(AB),它表示的是 A 、 B A、B A、B同时发生的概率除以 B B B发生的概率。
那么根据这个知识点,我们可以推出,对于给定 Y Y Y值,求 X X X的分布列的求法为: X 、 Y X、Y X、Y两个值都给定的概率(对照上面的说法),除以 Y Y Y给定值的概率(就是不管 X X X的值是多少),即 P { X = x i ∣ Y = y i } = P { X = x i , Y = y i } P { Y = y i } P\{X=x_{i}|Y=y_{i}\}=\frac{P\{X=x_{i},Y=y_{i}\}}{P\{Y=y_{i}\}} P{X=xi∣Y=yi}=P{Y=yi}P{X=xi,Y=yi}
是不是这样子捏?
又由上一节可以知道啊, P { X = x i , Y = y i } = p i j P\{X=x_{i},Y=y_{i}\}=p_{ij} P{X=xi,Y=yi}=pij, P { Y = y i } = p ⋅ j P\{Y=y_{i}\}=p_{·j} P{Y=yi}=p⋅j。于是
定义:对于给定的 j j j,在 Y = y j Y=y_{j} Y=yj条件下随机变量的条件概率分布为: P { X = x i ∣ Y = y i } = p i j p ⋅ j i = 1 , 2... P\{X=x_{i}|Y=y_{i}\}=\frac{p_{ij}}{p_{·j}}~~~~~~~~i=1,2... P{X=xi∣Y=yi}=p⋅jpij i=1,2...
同样,对于给定的 i i i,在 X = x i X=x_{i} X=xi条件下随机变量的条件概率分布为: P { Y = y j ∣ X = x i } = p i j p i ⋅ j = 1 , 2... P\{Y=y_{j}|X=x_{i}\}=\frac{p_{ij}}{p_{i·}}~~~~~~~~j=1,2... P{Y=yj∣X=xi}=pi⋅pij j=1,2...
☁️ 连续型随机变量的条件概率密度
注意注意噢!上一个标题是条件概率分布,这个标题是条件概率密度了,这是为啥?
概率分布是离散型随机变量的性质,概率密度是连续型随机变量的性质(把离散型和连续型分清楚就好了)。
对于一个随机变量的给定值,求它的概率在连续型这是行不通的,由连续型随机变量的性质可知:对任意 x , y x,y x,y, P { X = x } = 0 , P { Y = y } = 0 P\{X=x\}=0,P\{Y=y\}=0 P{X=x}=0,P{Y=y}=0。所以我们这里要把这个点扩散到一个范围,使它“连续”。也就是使这个点处于一个很小很小很小的一个范围内就行了。总之就是要使它有个范围!
定义:给定 y y y,设对于任意固定的 ϵ > 0 \epsilon >0 ϵ>0, P { y − ϵ < Y ≤ y + ϵ } > 0 P\{y-\epsilon
存在,则称此极限为在条件 Y = y Y=y Y=y下 X X X的条件分布函数,记为 P { X ≤ x ∣ Y = y } P\{X\leq x|Y=y\} P{X≤x∣Y=y}或 F X ∣ Y ( x ∣ y ) F_{X|Y}(x|y) FX∣Y(x∣y)。
同样注意注意!

到这里,我们先清楚清除,这期的标题:连续型随机变量的条件概率密度,据我所知,概率密度好像是一个类型 f ( x ) f(x) f(x)这样的“ f f f”开头的函数吧?
OK,从上面定义的结论可知,我们得到了条件分布函数,又由前面的知识可知啊,条件分布函数的导数就是概率密度函数(大概是这样,具体情况具体分析),也就是说有 F X ∣ Y ( x ∣ y ) = ∫ − ∞ x f X ∣ Y ( u ∣ y ) d u F_{X|Y}(x|y)=\int_{-\infty}^{x}f_{X|Y}(u|y)du FX∣Y(x∣y)=∫−∞xfX∣Y(u∣y)du
那么,这个 f X ∣ Y ( x ∣ y ) f_{X|Y}(x|y) fX∣Y(x∣y)就是我们要找的概率密度函数啦!(上面的 u u u是为了区分变量 x x x和值 x x x)
好了,真正的定义它来了!!
定义:设二维连续型随机变量 ( X , Y ) (X,Y) (X,Y)的概率密度函数为 f ( x , y ) f(x,y) f(x,y), Y Y Y的边缘概率密度函数为 f ( y ) f(y) f(y),若 f ( x , y ) f(x,y) f(x,y)在点 ( x , y ) (x,y) (x,y)处连续, f ( y ) f(y) f(y)在 y y y处连续,则有: f X ∣ Y ( x ∣ y ) = f ( x , y ) f ( y ) f_{X|Y}(x|y)=\frac{f(x,y)}{f(y)} fX∣Y(x∣y)=f(y)f(x,y)
同样的有: f Y ∣ X ( y ∣ x ) = f ( x , y ) f ( x ) f_{Y|X}(y|x)=\frac{f(x,y)}{f(x)} fY∣X(y∣x)=f(x)f(x,y)
这里就不对它们进行证明咯,有兴趣的大家下去了解吧!

随机变量的独立性
之前我们学过了两个随机事件的相互独立性,可表示为 P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B)
那么又来对比, P { X ≤ x , Y ≤ y } = P { X ≤ x } P { Y ≤ y } P\{X\leq x,Y\leq y\}=P\{X\leq x\}P\{Y\leq y\} P{X≤x,Y≤y}=P{X≤x}P{Y≤y},而这个式子又可以写成为 F ( x , y ) = F ( x ) F ( y ) F(x,y)=F(x)F(y) F(x,y)=F(x)F(y)
通常在题目中,有可能要根据 F ( x , y ) F(x,y) F(x,y)求 F ( x ) F(x) F(x)或 F ( y ) F(y) F(y),这里可以介样子求: F ( x ) = F ( x , + ∞ ) F(x)=F(x,+\infty) F(x)=F(x,+∞),然后带入 + ∞ +\infty +∞到 y y y中即可,同理可求得 F ( y ) F(y) F(y)。
(别问为啥要说一下这个,问就是今天做题想了半天)
由前面的知识可知,分布函数是随机变量(随机向量)的特性,也就是说适用于离散型和连续型,于是乎,下面又要分两种情况来介绍~~

不过这次就比较简单易懂了。
☁️ 离散型随即变量的独立性
依照随机事件的独立性直接给出公式: P { X = x i , Y = y i } = P { X = x i } P { Y = y i } P\{X=x_{i},Y=y_{i}\}=P\{X=x_{i}\}P\{Y=y_{i}\} P{X=xi,Y=yi}=P{X=xi}P{Y=yi}
☁️ 连续型随机变量的独立性
f ( x , y ) = f ( x ) f ( y ) f(x,y)=f(x)f(y) f(x,y)=f(x)f(y)
C语言实现案例
先来一个简单的练练手
- 设二维随机向量 ( X , Y ) (X,Y) (X,Y)的概率分布如下表所示,它的条件概率分布
| X\Y | 0 | 2 | 5 |
|---|---|---|---|
| 1 | 0.15 | 0.25 | 0.35 |
| 3 | 0.05 | 0.18 | 0.02 |
题目分析:做题的话这个题直接按照公式套就行了,十分简单
#include 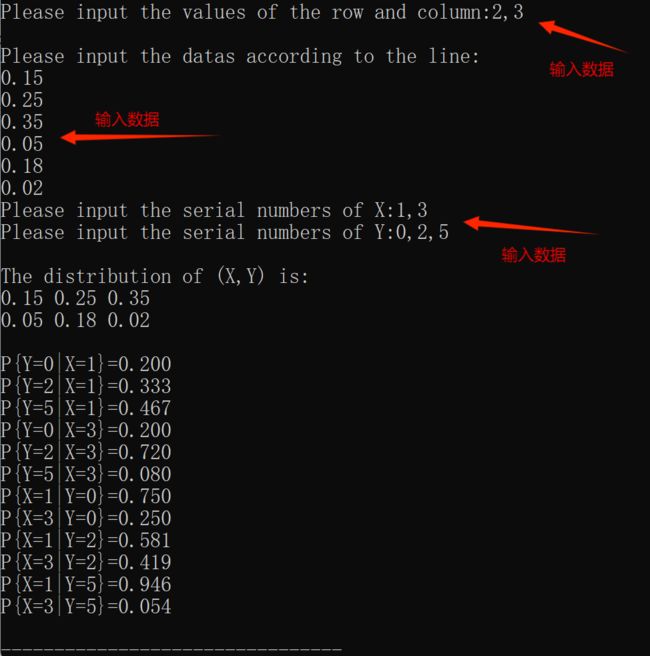
代码分析:整体来说代码都挺简单的,就是在输出的时候, X X X的值不是0,1而是1,3, Y Y Y的值不是0,1,2而是0,2,5。这里呢我们就需令设两个数组来存储它们的序号。
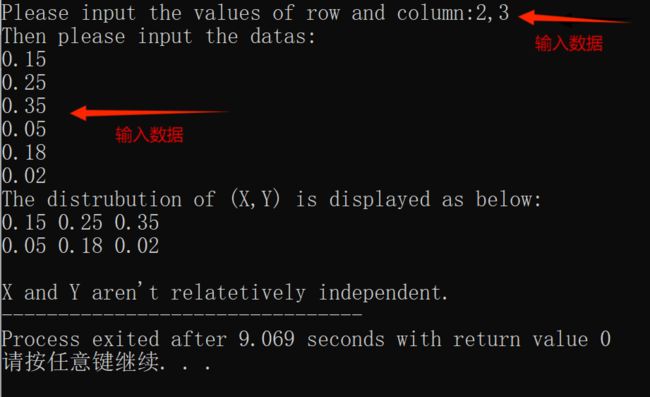
- 求上题中的 X X X和 Y Y Y是否相互独立?
题目分析:将数据带入公式判断即可。
#include