car | 线性回归（三）——残差分析和异常点检验

本篇介绍如何检验回归结果是否符合模型假设，以及样本中是否存在异常点。本篇使用的主要工具包是car，包名是Companion to Applied Regression的缩写，该包提供了许多用于模型检验的函数。

初始模型如下：

library(car)
library(dplyr)
DATA <- mtcars[, c("mpg", "wt", "qsec", "drat")]
model <- lm(mpg ~ wt + qsec, data = DATA)

4 残差分析

残差是因变量未被自变量解释的部分，线性模型要求残差服从独立同分布，且分布类型为正态分布。通过一系列方法判断残差是否符合这一要求，可以达到检验模型是否符合相应假设的目的。

4.1 模型残差的几种形式

帽子矩阵

帽子矩阵记为 ，有 。对于线性模型来说，

所以，

• 帽子矩阵只与设计矩阵 有关。

帽子矩阵是行数和列数都与样本数量相同的方阵，其对角线的元素称为对应样本的帽子值，记为 。

stats中计算帽子值的函数有hatvalues和hat：

## S3 method for class 'lm'
hatvalues(model, infl = lm.influence(model, do.coef = FALSE), ...)

hat(x, intercept = TRUE)

• hatvalues函数直接对模型对象使用；

• hat函数对 使用。

hatvalues(model) %>% head()

##         Mazda RX4     Mazda RX4 Wag        Datsun 710    Hornet 4 Drive 
##        0.06925986        0.04436414        0.06072636        0.05761138 
## Hornet Sportabout           Valiant 
##        0.03890382        0.09571739

X = cbind(c(rep(1, 32)), DATA$wt, DATA$qsec)
hat(X)

##  [1] 0.06925986 0.04436414 0.06072636 0.05761138 0.03890382 0.09571739
##  [7] 0.07290940 0.07910987 0.29502367 0.03576473 0.04604739 0.05607697
## [13] 0.04018415 0.04306089 0.17681412 0.20008504 0.18444635 0.08363669
## [19] 0.11801654 0.12264373 0.08877914 0.04244725 0.03524115 0.09660408
## [25] 0.04825977 0.09094506 0.09356216 0.15232675 0.14923442 0.10267260
## [31] 0.13793379 0.04159134

普通残差

普通残差的计算函数为：

residuals(object, ...)

标准化残差

由于模型的残差来自样本，而非总体，因此标准化残差不能由scale函数得到。

因为，

使用残差的标准差 代替 ，则标准化残差 ：

stats中计算标准化残差的函数为rstandard：

## S3 method for class 'lm'
rstandard(model, infl = lm.influence(model, do.coef = FALSE),
          sd = sqrt(deviance(model)/df.residual(model)),
          type = c("sd.1", "predictive"), ...)

• sd参数为残差的标准差，该函数默认的计算公式为总残差平方和除以残差自由度再开方。

deviance(model)

## [1] 195.4636

sum((fitted(model) - DATA$mpg)^2)

## [1] 195.4636

df.residual(model)

## [1] 29

rstandard(model) %>% head()

##         Mazda RX4     Mazda RX4 Wag        Datsun 710    Hornet 4 Drive 
##       -0.32543724       -0.01900129       -1.00443793       -0.07164647 
## Hornet Sportabout           Valiant 
##        0.19797699       -1.20244126

scale(residuals(model)) %>% head()

##                          [,1]
## Mazda RX4         -0.32461106
## Mazda RX4 Wag     -0.01920486
## Datsun 710        -1.00647043
## Hornet 4 Drive    -0.07191039
## Hornet Sportabout  0.20066887
## Valiant           -1.18221865

学生化残差

学生化残差的计算公式：

• 是去除第 个样本后估计的模型残差的标准差；

• 和 分别为样本个数和自变量个数。

stats中计算学生化残差的函数为rstudent：

## S3 method for class 'lm'
rstudent(model, infl = lm.influence(model, do.coef = FALSE),
         res = infl$wt.res, ...)

• res：模型残差。

rstudent(model) %>% head()

##         Mazda RX4     Mazda RX4 Wag        Datsun 710    Hornet 4 Drive 
##       -0.32036255       -0.01867092       -1.00459752       -0.07040658 
## Hornet Sportabout           Valiant 
##        0.19466525       -1.21213082

4.2 使用plot函数对模型进行诊断

基础绘图系统的plot函数输入对象为回归模型时，返回对象是四幅模型诊断图。

par(mfrow = c(2,2))
plot(model)

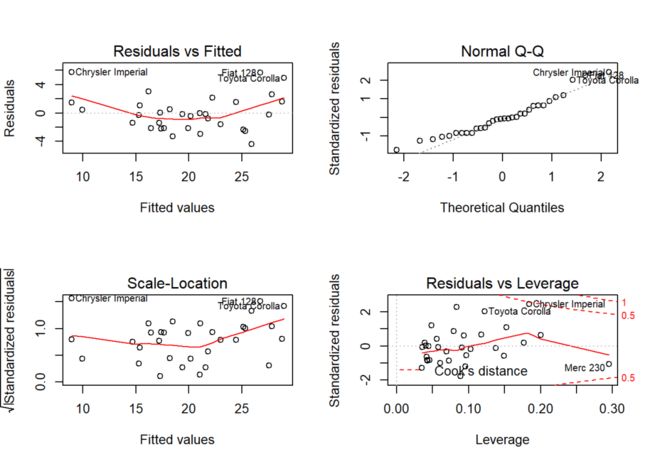
• 四幅图依次为残差-拟合图、正态Q-Q图、尺度-位置图、残差-杠杆图；

• 除残差-杠杆图用于检验异常点外，其余三幅图均用于检验模型结果是否符合假设。

残差-拟合图

模型拟合值与残差之间的散点图，红色线条表示二者关系的平滑曲线。若满足线性假设，二者应该不存在任何趋势性的关系，即红色线条应该与y = 0基本重合。但从图中观察，残差与拟合值可能具有二次函数关系，因此原模型线性假设可能不成立，可以考虑加入变量的二次项。

分别在模型中加入变量wt和qsec的二次项：

model.1 <- update(model, .~. + I(wt^2))
plot(model.1, 1) # 仅输出残差-拟合图

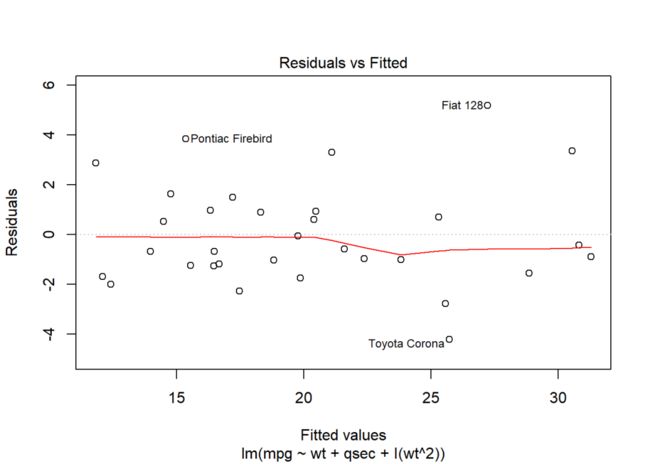
model.2 <- update(model, .~. + I(qsec^2))
plot(model.2, 1) # 仅输出残差-拟合图

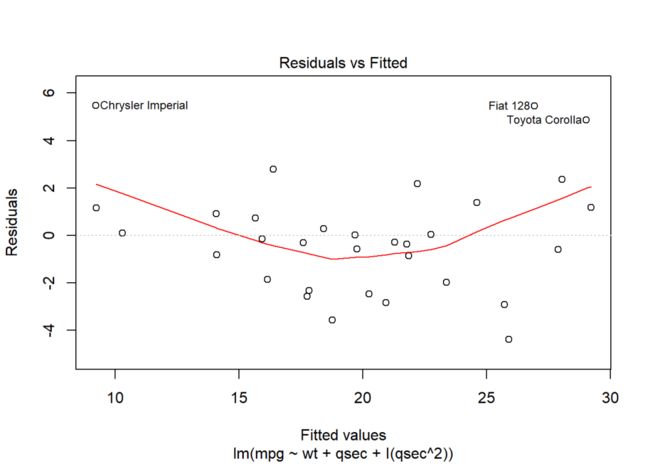
• 可以看出，model.1的残差-拟合图显示拟合值与残差无关，而model.2的结果显示二者仍然存在二次函数关系。因此，在模型中加入wt变量的二次项能使模型满足线性假设。

残差-拟合图的三种情况（薛毅，陈立萍. 统计建模与R软件[M]）：

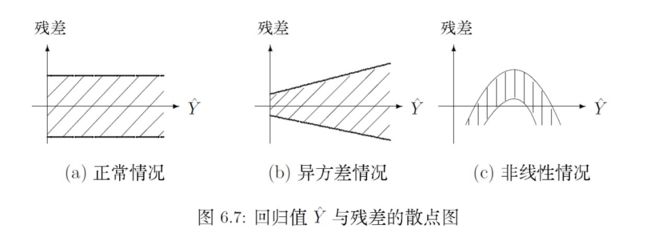
下文以model.1代替model：

model2 <- model.1

正态Q-Q图

Q-Q图可以检验数据序列是否满足某种概率分布，它将对应分布的概率分位数作为横坐标、数据序列的分位数作为纵坐标作成散点图，若该数据序列满足该概率分布，则散点的趋势线应该与某条直线基本重合。

这里正态Q-Q图检验的是标准化残差是否服从 ：

plot(model2, 2) # 只输出正态Q-Q图

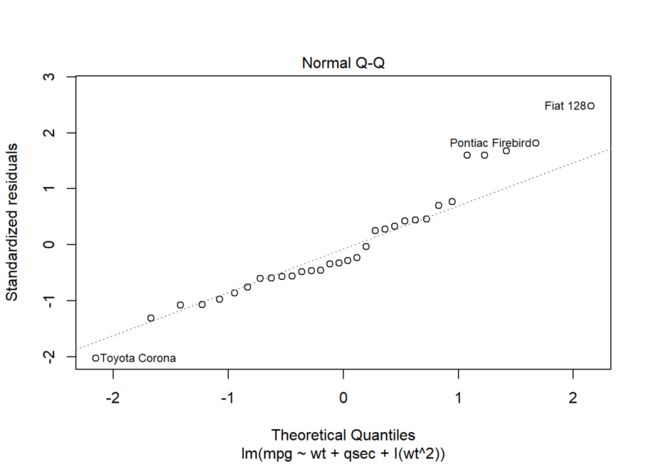
• 图中有文本标注的散点是与对应的标准分布的分位数相差较远的样本；

• 总体上看，model的残差能够满足正态分布。

尺度-位置图

若模型满足同方差假设，则拟合值处于不同位置时残差的分布范围应该基本相同，即没有明显的集聚性或离散性，这一点可以通过观察残差-拟合图散点的离散程度，但更直观地是通过观察尺度-位置图。该图的纵坐标为标准化残差绝对值的平方根。若满足假设，则趋势线应该基本呈水平状。

plot(model2, 3) # 只输出尺度-位置图

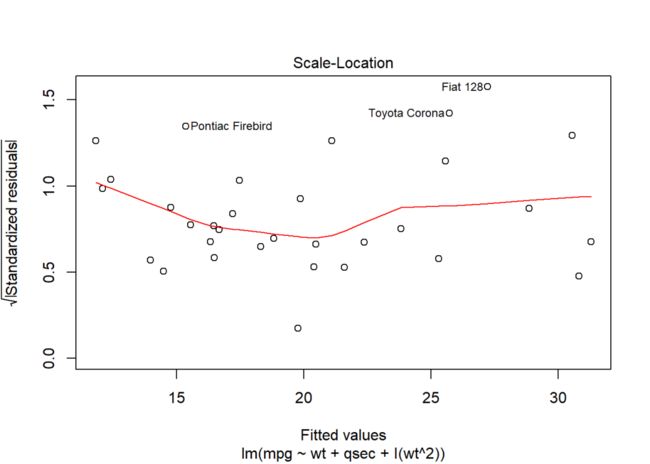
• 观察model的尺度-位置图可以发现，模型基本满足同方差性。

除了使用plot函数外，还可以使用car工具包的一些函数对线性模型进行诊断。

4.3 成分残差图——线性假设

成分残差图用于检验模型的线性假设，它描述的是自变量 和偏残差 之间的关系，又称偏残差图。偏残差的计算公式为：

式中 表示自变量标识， 表示样本标识。

偏残差实际上是将每个样本对应的残差分解给各个自变量。car工具包中偏残差图的绘制函数为crPlots。

绘制所有自变量的偏残差图：

crPlots(model2)

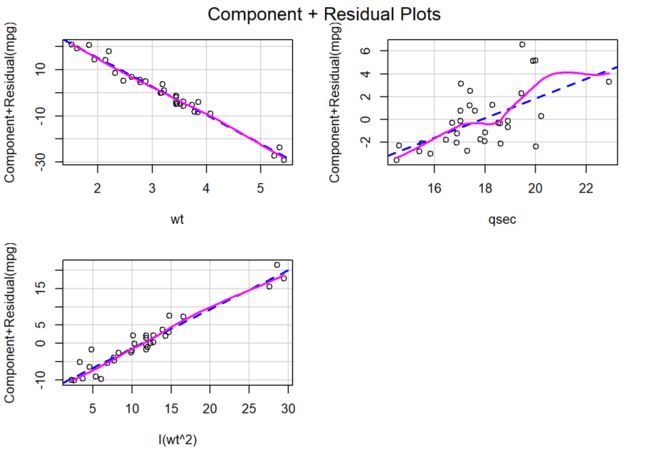
绘制指定自变量的偏残差图：

crPlot(model2, "wt")

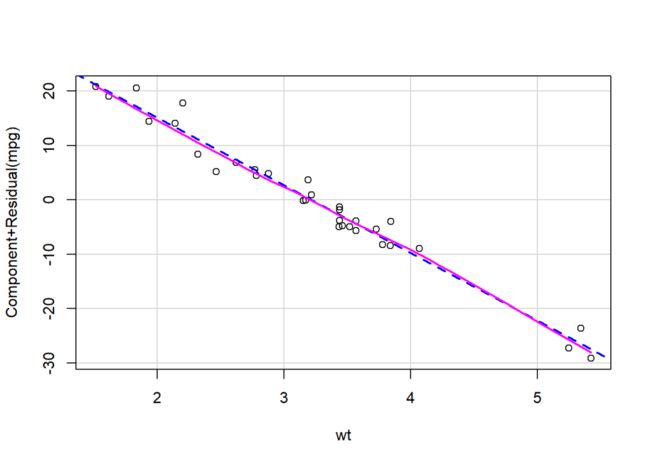
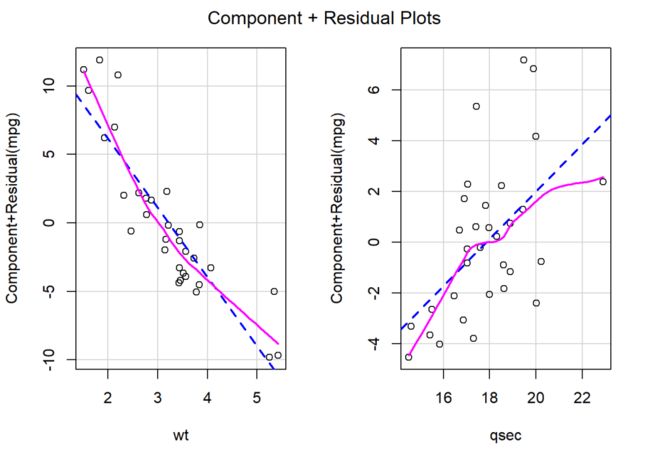
• 若模型符合线性假设，图中的紫红色曲线应该接近为一条直线；

• 由图可以看出，加入二次项后，wt和wt^2与因变量基本满足线性关系。

未加入wt变量二次项的模型的偏残差图：

crPlots(model)

4.4 Q-Q图——正态性假设

car工具包的qqPlot函数以线性模型为输入对象，可以输出Q-Q图。与plot函数不同的是，它是通过检验学生化残差是否服从t分布：

## S3 method for class 'lm'
qqPlot(x, xlab=paste(distribution, "Quantiles"),
    ylab=paste("Studentized Residuals(",
                deparse(substitute(x)), ")", sep=""),
    main=NULL, distribution=c("t", "norm"),
    line=c("robust", "quartiles", "none"), las=par("las"),
    simulate=TRUE, envelope=.95,  reps=100,
    col=carPalette()[1], col.lines=carPalette()[2], lwd=2, pch=1, cex=par("cex"),
    id=TRUE, grid=TRUE, ...)

• 相比于plot函数，该函数绘制的Q-Q图还带有置信区间，由envelope参数控制置信水平，默认为95%。

qqPlot(model2)

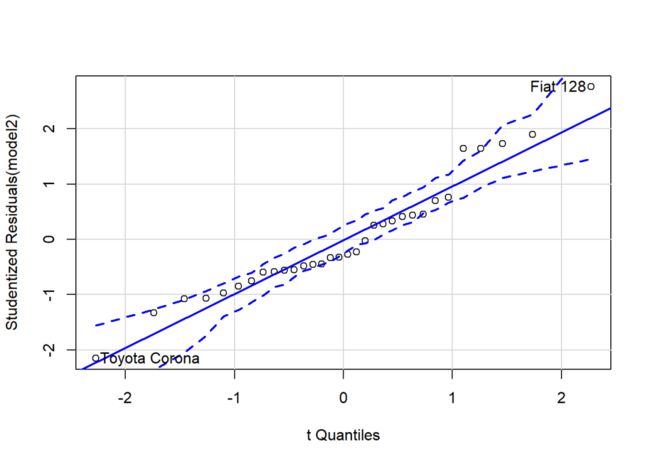
• 横坐标为t分布的分位数；纵坐标为学生化残差。

该函数也可以以数据序列为输入对象：

## Default S3 method:
qqPlot(x, distribution="norm", groups, layout,
    ylim=range(x, na.rm=TRUE), ylab=deparse(substitute(x)),
    xlab=paste(distribution, "quantiles"), glab=deparse(substitute(groups)),
    main=NULL, las=par("las"),
    envelope=.95, col=carPalette()[1], col.lines=carPalette()[2],
    lwd=2, pch=1, cex=par("cex"),
    line=c("quartiles", "robust", "none"), id=TRUE, grid=TRUE, ...)

• distribution：待检验的概率分布类型。

检验普通残差是否符合正态分布：

qqPlot(residuals(model2), envelope = 0.99)

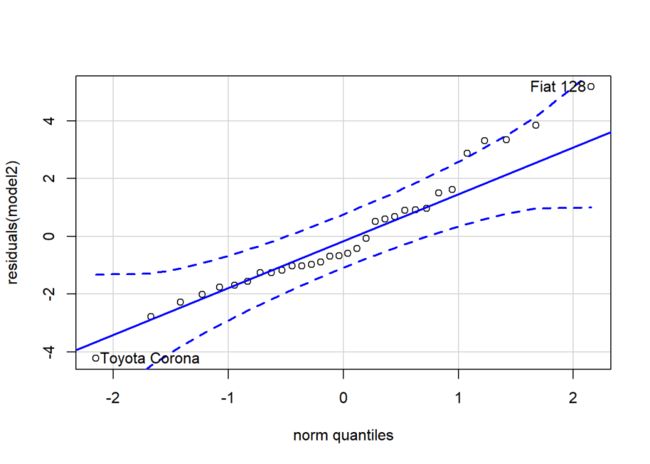
stats包也有相关函数可以绘制Q-Q图：

• qqnorm函数：专门绘制正态Q-Q散点图；

• qqline函数：专门绘制Q-Q直线图，默认为正态分布；

• qqplot函数：绘制两个序列之间的Q-Q散点图。

qqnorm(y, ylim, main = "Normal Q-Q Plot",
       xlab = "Theoretical Quantiles", ylab = "Sample Quantiles",
       plot.it = TRUE, datax = FALSE, ...)

qqline(y, datax = FALSE, distribution = qnorm,
       probs = c(0.25, 0.75), qtype = 7, ...)

qqplot(x, y, plot.it = TRUE, xlab = deparse(substitute(x)),
       ylab = deparse(substitute(y)), ...)

• qqnorm已经指定了横坐标为正态分布的分位数，因此只有y参数，而没有x参数；

• qqline通过distribution参数指定分布类型，也不需要x参数；

• qqplot没有指定的分布类型，同时有x和y两个参数。

qqnorm(residuals(model2))
qqline(residuals(model2))

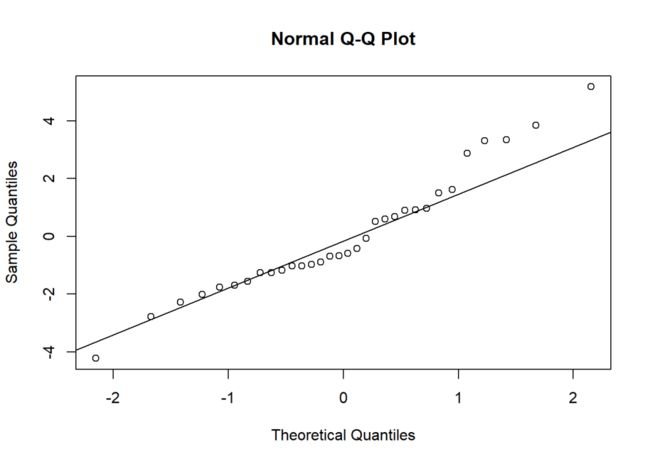
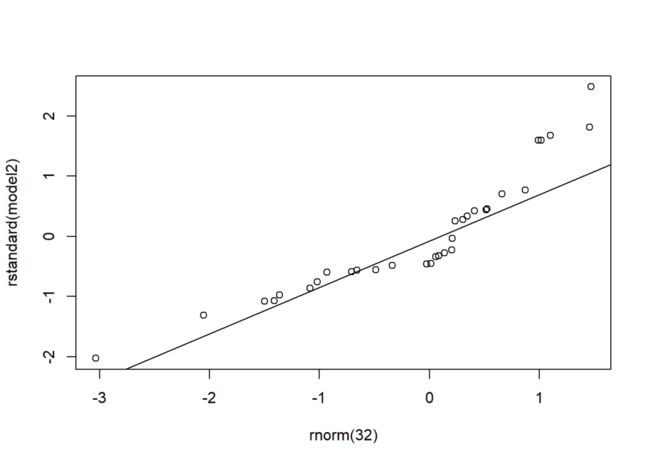
set.seed(234)
qqplot(x = rnorm(32), y = rstandard(model2))
qqline(rstandard(model2))

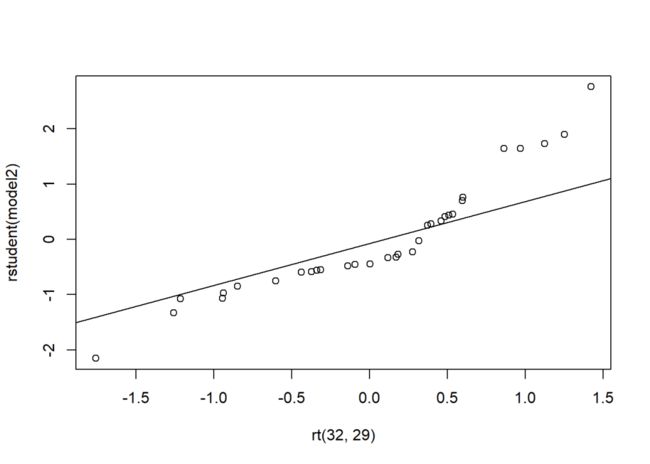
set.seed(234)
qqplot(x = rt(32, 29), y = rstudent(model2))
qqline(rstudent(model2))

除了通过Q-Q图外，还可以使用shapiro.test函数检验残差的正态性。该函数使用的是Shapiro-Wilk检验：

shapiro.test(residuals(model2))

## 
##  Shapiro-Wilk normality test
## 
## data:  residuals(model2)
## W = 0.95504, p-value = 0.2001

• 检验的原假设为样本分布服从正态分布。W和p值越大，越无法拒绝原假设。

4.5 异方差检验——同方差假设

car工具包中的ncvTest函数可以用来检验模型残差的方差是否为常数：

ncvTest(model, var.formula, ...)

ncvTest(model)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 0.590986, Df = 1, p = 0.44204

• 检验的原假设为方差是常数，备选假设为方差随拟合值而变化。

• 由于p > 0.05，可以认为原假设成立，模型符合同方差假设。

4.6 Durbin-Watson检验——独立性假设

car工具包中的durbinWatsonTest函数使用D-W检验判断残差是否存在一阶自相关，即检验模型是否符合独立性假设：

durbinWatsonTest(model2)

##  lag Autocorrelation D-W Statistic p-value
##    1      -0.1568836       2.30422    0.59
##  Alternative hypothesis: rho != 0

4.7 方差膨胀系数——多重共线性假设

方差膨胀系数（VIF）可以用来检验自变量之间是否具有多重共线性。自变量对应的VIF越大，说明其越有可能与其他自变量存在多重共线性。car工具包中的函数为vif：

vif(model2)

##        wt      qsec   I(wt^2) 
## 27.076669  1.039145 26.896784

• wt与wt^2之间具有较大的共线性。

5 异常点检验

异常点有如下三类：

• 离群点：模型残差的绝对值较平均水平大的点；

• 高杠杆点：对应的帽子值较大的点；

• 强影响点：对模型的估计结果会产生较大影响的点。

使用plot函数绘制的残差-杠杆图即用来检验以上异常点，实际上该函数可以绘制出3副用于检验异常点的图形：

plot(model2, c(4,5,6))

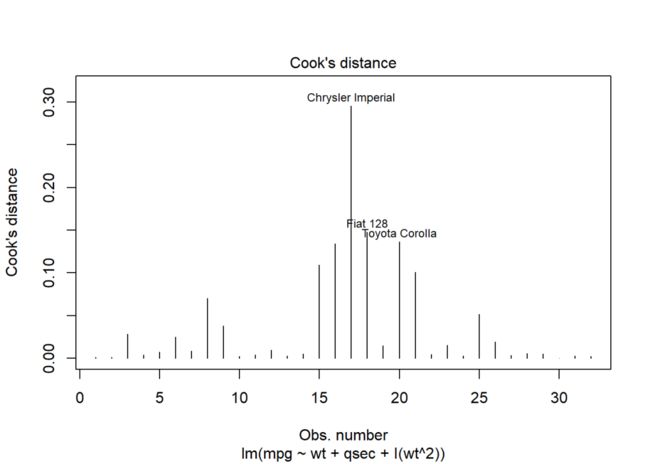
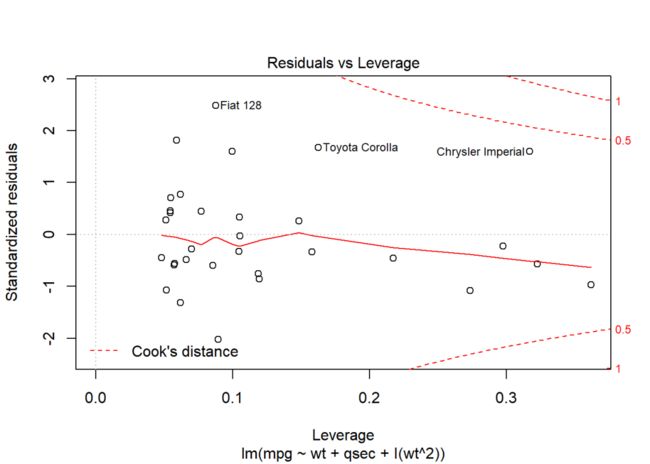
• 第2副图为残差-杠杆图，其横坐标为样本的杠杆值，纵坐标为标准化残差，红色实线为二者的趋势线，红色虚线表示等Cook距离线；横坐标过大的点为高杠杆点，纵坐标过大的为离群点，红色虚线外的点为强影响点。

• 第1副图为各样本对应的Cook距离；

• 第3副图为杠杆和Cook距离之间的关系图。

判断强影响点有很多种方式，plot采用的是Cook距离法，Cook距离越大，样本越有可能是强影响点。单独计算Cook距离的函数为cooks.distance：

## S3 method for class 'lm'
cooks.distance(model, infl = lm.influence(model, do.coef = FALSE),
               res = weighted.residuals(model),
               sd = sqrt(deviance(model)/df.residual(model)),
               hat = infl$hat, ...)

cooks.distance(model2) %>% head()

##         Mazda RX4     Mazda RX4 Wag        Datsun 710    Hornet 4 Drive 
##       0.001462204       0.001070445       0.028330950       0.004065321 
## Hornet Sportabout           Valiant 
##       0.007191579       0.024914520

使用influence.measures函数可以查看更多对强影响点的判断方法：

influence.measures(model, infl = influence(model))

• 该函数输出对象的数据结构为list。

influence.measures(model)$infmat %>% data.frame() %>% head()

##                         dfb.1_       dfb.wt     dfb.qsec        dffit    cov.r
## Mazda RX4         -0.066746016  0.045198462  0.053535052 -0.087391326 1.180659
## Mazda RX4 Wag     -0.002387037  0.001500934  0.001828698 -0.004022867 1.162549
## Datsun 710        -0.017983327  0.159314504 -0.050256031 -0.255437492 1.063638
## Hornet 4 Drive     0.010086430 -0.002027881 -0.011775541 -0.017408140 1.178309
## Hornet Sportabout  0.015324605  0.005310827 -0.015357764  0.039165267 1.151306
## Valiant            0.300358415 -0.111592643 -0.318621040 -0.394359983 1.053858
##                         cook.d        hat
## Mazda RX4         2.627038e-03 0.06925986
## Mazda RX4 Wag     5.587076e-06 0.04436414
## Datsun 710        2.174253e-02 0.06072636
## Hornet 4 Drive    1.046036e-04 0.05761138
## Hornet Sportabout 5.288512e-04 0.03890382
## Valiant           5.101445e-02 0.09571739

• dfb.*为去除该样本后的相应自变量的模型估计结果，如dfb.1_的第一行数值是去掉第一个样本后对模型截距的估计结果；

• dffit为基于拟合值的判断方法；

• cov.r为基于协方差比值的判断方法。

通过输出对象的is.inf元素查看对应样本是否为强影响点：

influence.measures(model)$is.inf %>% head()

##                   dfb.1_ dfb.wt dfb.qsec dffit cov.r cook.d   hat
## Mazda RX4          FALSE  FALSE    FALSE FALSE FALSE  FALSE FALSE
## Mazda RX4 Wag      FALSE  FALSE    FALSE FALSE FALSE  FALSE FALSE
## Datsun 710         FALSE  FALSE    FALSE FALSE FALSE  FALSE FALSE
## Hornet 4 Drive     FALSE  FALSE    FALSE FALSE FALSE  FALSE FALSE
## Hornet Sportabout  FALSE  FALSE    FALSE FALSE FALSE  FALSE FALSE
## Valiant            FALSE  FALSE    FALSE FALSE FALSE  FALSE FALSE

• TRUE表示该方法认为该样本是强影响点，FALSE表示认为该样本不是强影响点。

---