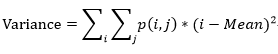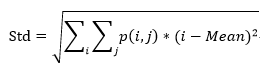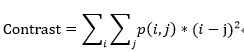图像特征(三)——纹理特征(GLCM、LBP)
转载请注明出处 https://mp.csdn.net/console/editor/html/105172768
接续上一节内容(形状特征),本文主要介绍纹理特征,并给出matlab上实现的demo。
纹理特征
纹理特征是一种全局特征,反映的是图像中同质现象的视觉特征,体现物体表面的具有缓慢变换或周期性变化的表面组织结构排列属性。图像纹理通过像素及其周围空间邻域的灰度分布来表现,即局部纹理信息。另外,局部纹理信息不同程度上的重复性,就是全局纹理信息。
纹理特征的提取方法可分为:(1)基于结构的方法,将要检测的纹理建模,在图像中搜索重复的模式。(2)基于统计数据的方法。
纹理特征的提取与匹配主要有:灰度共生矩阵、Tamura 纹理特征、自回归纹理模型、小波变换等。(1)灰度共生矩阵特征提取与匹配主要依赖于能量、惯量、熵和相关性四个参数。(2)Tamura 纹理特征基于人类对纹理的视觉感知心理学研究,提出6种属性,即:粗糙度、对比度、方向度、线像度、规整度和粗略度。(3)自回归纹理模型(simultaneous auto-regressive, SAR)是马尔可夫随机场(MRF)模型的一种应用实例。
灰度共生矩阵(Gray-level Co-occurrence Matrix, GLCM)
灰度共生矩阵(GLCM)的统计方法是20世纪70年代初由R.Haralick等人提出的,它是在假定图像中各像素间的空间分布关系包含了图像纹理信息的前提下,提出的具有广泛性的纹理分析方法。
图像I(N*N) 的任意一点f(x,y) 与其偏离点f(x+a,y+b) ,设该点对的灰度值为(g1,g2) 。令点f(x,y) 在整个图像上移动,便得到所有(g1,g2) 的值。假设灰度值的级数为k,则(g1,g2) 共有k2 种组合。对整个画面,统计每种(g1,g2) 值出现的次数,排列为方阵并将其归一化,这个方阵称为灰度共生矩阵。
差分值的选取:距离差分值(a,b) 取不同的数值组合,可得到不同情况下的联合概率矩阵。通常(a,b) 是按照纹理周期分布的特性来选择的,对于较细的纹理,选取1,0,0,1,(2.0) 等较小的差分值。
| a=1,b=0 |
像素对水平 |
0度扫描 |
|
a=1,b=1 |
右对角线 |
45度扫描 |
| a=0,b=1 |
像素对垂直 |
90度扫描 |
|
a=-1,b=-1 |
左对角线 |
135度扫描 |
两个像素灰度级同时发生的概率,就将(x,y) 空间坐标转换为“灰度对“(g1,g2) 的描述,便形成了灰度共生矩阵。
通过举例来说明:
示例1:参考博文https://blog.csdn.net/qq_37059483/article/details/78292869
![]()
GLCM表是所有像素可能的组合,如GLCM(1,1)是图像I中像素值为1和1的组合;GLCM(4,5)是图像I中像素值为4和5的组合。GLCM(i,j) 的值表示:图像I中像素值为i与像素值为j相邻的个数。相邻的规则:f(x,y) 和f(x+a,y+b) 相邻,是指x相邻a个单位、y相邻b个单位。
示例2:参考博文https://www.jianshu.com/p/91204c2771a8
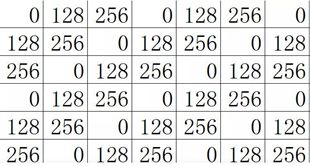
(1) 假设原图及对应的灰度值如下:
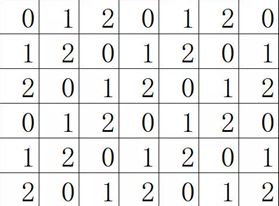
(2) 对灰度等级进行压缩(256 -> 3)
(3) 像素对位置关系
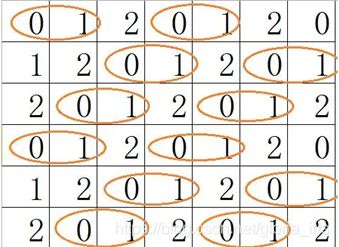
设定该图像是3阶的,所以GLCM是3阶方阵。δ 表示像素对的位置关系(如水平、垂直、45度、-45度)。
图中(i,j)表示两个像素的灰度等级;n(i,j) 表示在δ 定义的位置关系下,该像素对出现的次数。如n(0,0), δ 为水平,(0,0)像素在灰度图中出现的次数为0;n(0,1), δ 为水平,(0,1)像素在灰度图中出现的次数为0。
(4) 结果,最后得到的GLCM如下:
Demo
function out = GLCMatrix(img, offset, n1)
% 输入: img:输入图像
% offset:偏移量
% n1:图像中包含的像素值个数
% 输出:偏移量为offset的灰度共生矩阵
s = size(img);
[r, c] = meshgrid( 1:s(1), 1:s(2) );
r = r(:);
c = c(:);
r2 = r + offset(1);
c2 = c + offset(2);
% 去掉下表超出图像边界的像素和他的邻接像素
bad = c2<1 | c2>s(2) | r2<1 | r2>s(1) ;
index = [ r c r2 c2 ];
index(bad, :) = [];
% 分别以(r,c)和(r2,c2)为索引扎到图像img中对应的像素值向量(v1, v2)
v1 = img( sub2ind(s, index(:,1), index(:,2)) );
v2 = img( sub2ind(s, index(:,3), index(:,4)) );
v1 = v1(:);
v2 = v2(:);
ind = [v1 v2];
bad = v1~=v2 ; % 去掉像素值不相同的行
ind(bad, :) = [];
if isempty(ind)
oneGLCM2 = zeros(n1);
else
% 计算v1和v2相同的像素对数,并用n1*n1矩阵列出来
oneGLCM2 = accumarray( ind+1, 1, [n1, n1] );
end
out = [];
for i = 1:n1
out = [ out oneGLCM2(i,i) ];
end
out = out(:);
end统计特性
灰度共生矩阵虽然提供了图像灰度方向、间隔和变化幅度的信息,但它不能直接提供区别纹理的特性,因此需要在GLCM的基础上计算用来定量描述纹理特征的统计属性——常用的9种纹理特征统计属性为:
LBP特征
LBP(Local Binary Pattern,局部二值模式)是一种用来描述图像局部纹理特征的算子;它具有旋转不变性和灰度不变性等显著的优点。它是首先由T. Ojala, M.Pietikäinen, 和D. Harwood 在1994年提出,用于纹理特征提取
LBP算法的核心思想,是以某个像素点为中心,与其邻域像素点共同计算。关于邻域像素点的选择方法,其实并不唯一:
- 原始的LBP算子定义的是在3*3的窗口内,以窗口中心像素为阈值,将相邻的8个像素点灰度值与其进行比较;
- 后来的LBP算法也将相邻8个像素点的位置改成了环形邻域内8个点(也可能是环形邻域多个点),进行顺时针或逆时针的比较。
选择环形邻域的方法进行说明:
窗口中心的像素点作为中心,该像素点的像素值作为阈值。然后将周围8个像素点的灰度值与该阈值进行比较,若周围某像素值大于中心像素值,则该像素点位置被标记为1;反之,该像素点标记为0。
如此这样,该窗口的8个点可以产生8位的无符号数,这样就得到了该窗口的LBP值,该值反应了该窗口的纹理信息。如下图所示:
算法流程:
LBP纹理特征向量,一般以图像分块LBP直方图表示。具体步骤如下:
(1) 图像划分若干为N × N的图像子块(如16 × 16),计算每个子块中每个像素的LBP值;
(2) 对每个子块进行直方图统计,得到N × N图像子块的直方图;
(3) 对所有图像子块的直方图进行归一化处理;
(4) 连接所有子块的归一化直方图,便得到了整幅图像的纹理特征。
得到了整幅图像的LBP纹理特征后,便可以利用SVM或者其他机器学习算法进行分类了。
Demo
oriImg = imread('lena.tiff');
grayImg = rgb2gray(oriImg);
[m,n] = size(grayImg);
Features = zeros([m,n]);
for i = 2:m-1
for j = 2:n-1
% 得到领域,比较信息
neighbor = [ oriImg(i-1, j-1) oriImg(i-1, j) oriImg(i-1, j+1) oriImg(i, j-1)...
oriImg(i, j+1) oriImg(i+1, j-1) oriImg(i+1,j) oriImg(i+1, j+1)] ...
> oriImg(i,j);
pixel = 0;
for k = 1:8
pixel = pixel + neighbor(1,k)*bitshift(1,8-k); % 将其转换为十进制
end
Features(i,j) = pixel;
end
end
Features = uint8(Features);
figure; imshow(Features)