【数据挖掘】数据预处理

现实生活中的数据极易收到噪声、缺失值和不一致数据的影响。数据预处理是数据挖掘过程中的第一个步骤，主要有数据清洗、数据集成、数据归约和数据变换等方式。

一、数据预处理的必要性

---

数据的质量决定了数据挖掘的效果。而在原始数据中，大多数据都是Dirty数据，他们存在以下几个方面的问题。

• 数据不一致
• 噪声数据
• 缺失值

那，既然数据如此重要，我们就需要一套体系来评估数据的好坏不是吗

1️⃣ 准确性

数据记录是否存在异常或者误差

2️⃣ 一致性

数据是否符合某一规则

3️⃣ 完整性

是否存在确实

4️⃣ 时效性

能否及时更新

5️⃣ 可信性

用户可以信赖的数据

6️⃣ 可解释性

是否易于理解

---

二、数据清洗

2.1 数据清洗方法

1️⃣ 缺失值处理

• 忽略元组
• 人工填写缺失值
• 使用常量填充缺失值
• 使用中心趋势度填充缺失值
• 采用均值或者中位数填充
• 利用最可能的值进行填充

---

2️⃣ 噪声数据处理

• 分箱–借助邻域来光滑数据值
• 回归–采样函数来拟合光滑数据
• 离去点分析

---

2.2 基于Pandas进行数据清洗

1️⃣ 检测与处理缺失值

检测非空值

.isnull()

统计非空值

.isnull().sum()

查看非空值

df.info()

---

2️⃣ 缺失值处理

️ 删除

dropna()

dropna()对于Series，会返回一个仅含非空数据和索引的Series，而对于一个DataFrame对象，则会默认丢弃任何含有缺失值的行。

参数	说明
axis	0是行 1是列
how	确认缺失值的个数，'any’表示只要有缺失值就丢了,'all’则要全部
thresh	可以确定缺失值阈值
subset	只对子列进行操作，例如subset=[‘a’,'b]
inplace	不返回

️ 填充

fillna()

参数	说明
value	用于填充缺失值的标量值或者字典对象
method	插值方法
axis	待填充的轴
inplace	原地修改
limit	可以连续填充的最大数量

举个栗子

fillna()可以通过字典的方式进行填充。

df=pd.DataFrame(np.random.randn(5,3))
df.iloc[:3,1:]=pd.NA
print(df)
print(df.fillna({1:0.1,2:0.2}))

          0         1         2
0  0.078301      <NA>      <NA>
1  1.310107      <NA>      <NA>
2  0.025339      <NA>      <NA>
3  0.011049 -0.053258 -0.259365
4  0.664727  0.023836 -2.092003
          0         1         2
0  0.078301  0.100000  0.200000
1  1.310107  0.100000  0.200000
2  0.025339  0.100000  0.200000
3  0.011049 -0.053258 -0.259365
4  0.664727  0.023836 -2.092003

使用均值填充：

data.fillna(data.mean())

---

3️⃣ 数据值替换

通过relpace()方法进行替换

data={'姓名':['张三','小明','马芳','国志'],'性别':['0','1','0','1'],
      '籍贯':['北京','甘肃','','上海']}
df=pd.DataFrame(data)
df=df.replace('','我是你爹')
print(df)

   姓名 性别    籍贯
0  张三  0    北京
1  小明  1    甘肃
2  马芳  0  我是你爹
3  国志  1    上海

当然，也可以通过传入列表的方式进行多列更改：

df=df.replace(["我是你爹","北京"],["北京","PK"])
print(df)

哦提一嘴，这里需要接收！！

   姓名 性别  籍贯
0  张三  0  PK
1  小明  1  甘肃
2  马芳  0  北京
3  国志  1  上海

不难发现，第一个列表是需要替换的值，第二个列表是替换后的值，且他们之间是并行的！不能链式替换~

也可以通过字典实现多值替换

df=df.replace({"1":"男","0":'女'})
print(df)

   姓名 性别  籍贯
0  张三  女  PK
1  小明  男  甘肃
2  马芳  女  北京
3  国志  男  上海

通过自定义函数map实现~！

data={'姓名':['张三','小明','马芳','国志'],'性别':['0','1','0','1'],
      '籍贯':['北京','甘肃','','上海']}
df=pd.DataFrame(data)
df['成绩']=[58,62,71,99]

def grade(x):
    if x>=90:
        return "优"
    if x>=80:
        return "良"
    if x>=60:
        return "及格"
    else:
        return "不及格"

df['成绩']=df['成绩'].map(grade)
print(df)

   姓名 性别  籍贯   成绩
0  张三  0  北京  不及格
1  小明  1  甘肃   及格
2  马芳  0       及格
3  国志  1  上海    优

---

4️⃣ 异常值检测

散点图

wdf=pd.DataFrame(np.arange(20),columns=['W'])
wdf['Y']=wdf['W']*1.5+2
wdf.iloc[3,1]=128
wdf.iloc[18,1]=150
wdf.plot(kind='scatter',x='W',y='Y')
plt.show()

箱线图

plt.boxplot(wdf['Y'].values,notch=True)
plt.show()

3$\sigma$法则

数据服从正态分布时，在$3\sigma$法则下，异常值被定义为一组测定值中与均值偏差超过三倍标准差$\sigma$的值。因为在正态分布下，距离均值$3\sigma$之外的值出现的概率小于$0.003$，可看做小概率时间。

def outRange(S):
    blidx=(S.mean()-3*S.std()>S)|(S.mean()+3*S.std()<S)
    idx=np.arange(S.shape[0])[blidx]
    outRange=S.iloc[idx]
    return outRange
print(outRange(wdf['Y']))

18    150.0
Name: Y, dtype: float64

值得注意的是啊，像这种表达式

S.mean()-S.std()>S

会返回有个只有True或者False的Series，也就是0,1。此时可以用位运算|保留1的结果。

但是拿到了Series，我们还要原始数据呐不是，所以还需要获取原始数据

idx=np.arange(S.shape[0])[blidx]
S.iloc[idx]

---

2.3 数据集成

有时候需要挖掘的数据可能来自多个数据源，导致数据存在冗余与不一致的情况。数据集成是将多个数据源中的数据合并，并存放到一个一致的数据存储中。

1️⃣ 数据冗余和相关性分析

冗余是数据继承的重要问题，如果一个属性能由另一个属性或者另一组属性值推导而出，那么这个属性可能就是冗余的哦。此外，属性命名不一致也会导致冗余。

我们下面介绍如何判断属性是不是冗余的哈！

---

${\chi }^2$检验

卡方检验适用于标称属性，假设对于两个属性$A,B$,$A$有$c$个不同的取值，$B$有$r$个不同的取值，用$A$和$B$描述的数据元组可以用一个相依表显示，其中$A$的$c$个值构成列，$B$的$r$个值构成行。$(A_i,B_j)$表示属性$A$取$i$，属性$B$取$j$的联合事件。
$${\chi }^2=\sum _{i=1}^c\sum _{j=1}^c\frac{(o_{ij}-e_{ij}{)}^2}{e_{ij}}$$
其中$O_{ij}$表示联合事件的观测频度，$e_{ij}$表示期望频度，计算式为：
$$e_{ij}=\frac{count(A=a_i)\times count(B=b_j)}{n}$$
$n$为元组个数。

---

相关系数

又称为皮尔逊矩阵系数(Pearson)，相关系数$r_{A,B}$可定义为：
$$r_{A,B}=\frac{{\sum }_1^n(a_i-\bar{A})(b_i-\bar{B})}{n{\sigma }_A{\sigma }_B}=\frac{{\sum }_1^n(a_i{b}_j)-n\bar{A}\bar{B}}{n{\sigma }_A{\sigma }_B}$$
其中$n$为元组个数，$\bar{A}$为均值，$\sigma$为标准差，$a_i,b_i$为元组$i$在$AB$上的取值。

若$AB$独立，则$r_{A,B}=0$，取值范围为$-1,1$

---

协方差
$$Cov(X,Y)=E[(X-E(X))(Y-E(Y))]=E(XY)-E(X)E(Y)$$
实现

df.A.cov(df.B)
df.A.corr(df.B)

协方差反映二者趋势程度，取值没有界定，而相关系数则是将其标准化后评估趋近程度，具有取值界定。

---

2️⃣ 基于Pandas进行数据合并

merge()

例如

pd.merge(a,b,left_on="fruit",right_on="green",how="left")

在合并过程中可能或出现重复列名，我们可以通过suffixes进行修改

pd.merge(left,right,on="key1",suffixes=('_left','_right'))

---

concat()

例如

pd.concat([data1,data2],axis=0,join="inner",sort="False")

---

如果需要合并的两个DF存在重复索引，那么前面两个函数将无法正确合并，我们可以使用combine_first()进行合并，该方法会优先考虑第一个值。

---

2.4 数据标准化

由于量纲的问题，不同特征之间可能会产生较大的影响。为此，往往需要对数据进行标准化处理。

1️⃣ 离差标准化

做一个简单的线性变化，将数据映射到$[0,1]$
$$x_1=\frac{x-min}{max-min}$$

2️⃣ 标准差标准化

又称零均值标准化或$z$分数标准化，处理后的均值为$0$，标准差为$1$
$$x_1=\frac{x-mean}{std}$$

---

2.5 数据归约

Data Reduction是指在尽可能保证数据完整性的基础上得到数据的归约表示。也就是说，在归约后的数据集上挖掘更加有效，且会产生相同或相似的结果。

1️⃣ 维归约

减少随机变量或属性的个数，常见的方法有：

• 属性子集选择
• 小波变换
• 主成分分析

---

属性子集选择

通过删除不相关或冗余属性减少数据量，旨在找出最小属性集，使其分布尽可能接近原始分布。

如何选择一个好的子集？穷举是不显示的，所以一般使用压缩空间的启发式算法进行最优子集选取。

基本的启发式算法包含以下技术：

• 逐步向前选择
  • 也就是状态移动
• 逐步向后删除
  • 末位淘汰
• 选择+删除
  • 混合
• 决策树归纳

---

小波变换

这玩意继承和发展了短时傅里叶变换局部化的思想，又克服了窗口大小不随频率变化等缺点。能提供一个随频率改变的时间-频率窗口，是进行信号时频分析和处理的理想工具。

一般在频域，信号能量主要集中在低频，可以截取中低频系数保留近似的压缩数据。

---

主成分分析

PCA搜索$k$个最能代表数据的$n$维正交向量，是最常使用将为方法。

核心思想是找到数据里最主要的方面代替原始数据。

步骤

• 对样本中心化$x(i)=x(i)-\frac{1}{m}{\sum }_{j=1}^{m}x(j)$
• 计算样本的协方差矩阵$x{x}^T$
• 对协方差矩阵进行特征分析
• 取出最大的$n$个特征值对应的特征向量$(w_1,w_2,...,w_n)$，将所有的特征向量标准化后，组成特征向量矩阵$W$
• 将每个样本通过特征向量矩阵转化为新的样本，并得到样本集$z(i)=W^{T}x(i)$

尝试

对鸢尾花数据集进行降维

import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

data=load_iris()
y,x=data.target,data.data

pca=PCA(n_components=2)
reduced_x=pca.fit_transform(x)

# 绘出降维后的样本点分布
red_x,red_y=[],[]
blue_x,blue_y=[],[]
green_x,green_y=[],[]

for i in range(len(reduced_x)):
    if y[i]==0:
        red_x.append(reduced_x[i][0])
        red_y.append(reduced_x[i][1])
    elif y[i]==1:
        blue_x.append(reduced_x[i][0])
        blue_y.append(reduced_x[i][1])
    else:
        green_x.append(reduced_x[i][0])
        green_y.append(reduced_x[i][1])
plt.scatter(red_x,red_y,c='r',marker='X')
plt.scatter(blue_x,blue_y,c='b',marker='D')
plt.scatter(green_x,green_y,c='g',marker='.')
plt.show()

---

2️⃣ 数量归约

用较小、替代的数据表示原始数据。

• 回归和对数线性模型
• 直方图
• 积累
• 抽样
• 数据立方体聚类
• 数据压缩

---

2.6 数据变换与数据离散化

数据变换是一种将原始数据变化为比较合适的数据格式的方法，以便作为数据处理前特定数据挖掘算法的输入。

数据离散化则是一种数据变化的形式。

数据变换的策略

1️⃣ 光滑

2️⃣ 属性构造

3️⃣ 聚集

4️⃣规范化

5️⃣ 离散化

用于将概念标签递归组织成更高层的概念，形成数值属性的概念分层，以便不同用户需要

• 分箱离散化
  • 基于指定的箱个数的自顶向下的分裂技术，例如使用等宽或等频分箱，再通过箱均值或者中位数替换箱中的每个值，使得属性值离散化。
• 直方图离散化
  • 可以按照规定生成直方图，并且递归调用产生概念级
• 聚类、决策树、相关性分析进行离散化

---

Python数据变化与离散化

1️⃣ 数据规范化

import pandas as pd
import numpy as np

a=[47,83,81,18,72,41]
b=[56,96,84,21,87,67]

data=np.array([a,b]).T
df=pd.DataFrame(data,columns=["A","B"])
print("离差标准化: ",(df-df.min())/(df.max()-df.min()))
print("标准差标准化: ",(df-df.mean())/df.std())

离差标准化:            A         B
0  0.446154  0.466667
1  1.000000  1.000000
2  0.969231  0.840000
3  0.000000  0.000000
4  0.830769  0.880000
5  0.353846  0.613333

标准差标准化:            A         B
0 -0.386103 -0.456223
1  1.003868  1.003690
2  0.926648  0.565716
3 -1.505803 -1.733646
4  0.579155  0.675209
5 -0.617765 -0.054747

---

2️⃣ 哑变量处理

pd.get_dummies(df)

3️⃣ 连续变量的离散化

等宽法

pd.cut(x,bins,right=True,labels=None,retbins=False,precision=3)

举个栗子

np.random.seed(666)
score_list=np.random.randint(25,100,size=10)
print("原始数据",score_list)
bins=[0,59,70,80,100]
score_cut=pd.cut(score_list,bins)
print(pd.value_counts(score_cut))
c=pd.get_dummies(score_cut)
print(c)

原始数据 [27 70 55 87 95 98 55 61 86 76]
(80, 100]    4
(0, 59]      3
(59, 70]     2
(70, 80]     1
dtype: int64
   (0, 59]  (59, 70]  (70, 80]  (80, 100]
0        1         0         0          0
1        0         1         0          0
2        1         0         0          0
3        0         0         0          1
4        0         0         0          1
5        0         0         0          1
6        1         0         0          0
7        0         1         0          0
8        0         0         0          1
9        0         0         1          0

等频法

def SameRateCut(data,k=2):
    w=data.quantile(np.arange(0,1+1.0/k,1.0/k))
    data=pd.cut(data.w)
    return data

简单介绍一下这个方法啊，quantile表示返回指定位置$q$的百分位数，通过这个方法生成等频率。

---

聚类分析法

简单来说，有两步：

• 将连续性数据用聚类算法进行聚类，处理聚类得到的簇
• 为合并到一个簇的连续性数据做统一标记

---

2.7 基于scikit-learn进行数据预处理

1️⃣ 数据标准化与缩放

这边有一个api

sklearn.preprocessing.scale(X,axis=0,with_mean=True,with_std=True,copy=True)

实际作用

import sklearn.preprocessing as pre
import numpy as np

x_train=np.array([[1.,-2.,1.5],[2.2,1.3,0.5],[0.3,1.,-1.5]])
x_scaled=pre.scale(x_train)
print("均值: ",x_scaled.mean(axis=0))
print("标准差: ",x_scaled.std(axis=0))

均值:  [0. 0. 0.]
标准差:  [1. 1. 1.]

此外，pre模块还提供了一个实用程序类StandardScaler，可以记录训练时的参数，以便进行相同的转换。

scale=pre.StandardScaler().fit(x_train)
scale.transform(x_test)

2️⃣ 特征缩放

这里介绍三个API

pre.MinMaxScaler() # 范围为[0,1]
pre.MaxAbsScaler() # 范围为[-1,1]
pre.RobustScaler() # 适用于异常值较多

3️⃣ 非线性变换

非线性变换分为分位数变换和幂变换。二者都能保证每个特征值的秩。分位数变换将所有特征置于相同的期望分布中，而幂变换则是将数据从任意分布映射到接近高斯分布的位置。

映射到[0,1]均匀分布

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
import matplotlib.pyplot as plt

X,y=load_iris(return_X_y=True)
X_train,X_test,Y_train,Y_test=train_test_split(X,y,random_state=0)

# 分位数变换
quantile_transformer=preprocessing.QuantileTransformer(random_state=0)
X_train_trans=quantile_transformer.fit(X_train)
X_test_trans=quantile_transformer.transform(X_test)

# 查看分布
fig,ax=plt.subplots(1,2)
ax[0].hist(X_test_trans)
ax[1].hist(X_train)
plt.show()

映射到高斯分布

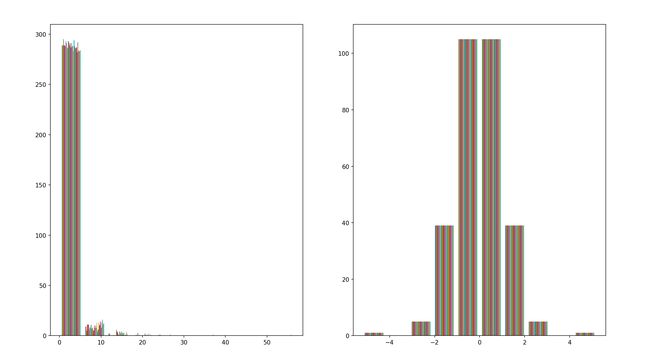
高斯分布具有稳定的方差和最小化偏度，PowerTransformer提供了两种幂变换：Yeo-Johnson和Box-Cox变换，Box-Cox仅可用于严格的政数局，这两种变换均通过lambda进行参数化，通过最大似然进行估计。

pt=preprocessing.PowerTransformer(method='box-cox',standardize=False)
X_lognormal=np.random.RandomState(616).lognormal(size=(300,30))
fig,ax=plt.subplots(1,2)
ax[0].hist(X_lognormal)

T=pt.fit_transform(X_lognormal)
ax[1].hist(T)
plt.show()

映射到正态分布

这里我们调用QuantileTransformer(output_distribution="normal")

pt=preprocessing.QuantileTransformer(output_distribution="normal")
X_lognormal=np.random.RandomState(616).lognormal(size=(300,30))
fig,ax=plt.subplots(1,2)
ax[0].hist(X_lognormal)

T=pt.fit_transform(X_lognormal)
ax[1].hist(T)
plt.show()

---

4️⃣ 正则化

正则化是将单个样本缩放到单位范数中(每个样本范数为1)，如果计划使用点积或者其他核的二次形式量化任意一堆样本的相似性，此过程可能会很有用。通常使用于文本分类和聚类中。
$$make||a||=1$$

x=[[1.,-1.,2.],[2.,0.,0.],[0.,1.,-1.]]
# l2正则化
x_nor=preprocessing.normalize(x,norm="l2")
print(x_nor)

[[ 0.40824829 -0.40824829  0.81649658]
 [ 1.          0.          0.        ]
 [ 0.          0.70710678 -0.70710678]]

同样也有一个Normalizer类，可以通过TransformerAPI实现相同操作。

---

5️⃣ 编码分类特征

如果要把定性数据转化为整数，可以使用OrdinalEncoder，该估计其可以将每个范畴特征转换为整数的一个新特征。

enc=preprocessing.OrdinalEncoder()
x=[['m','g','17'],['fm','r','22']]
enc.fit(x)
print(enc.transform([['fm','r','17']]))

[[0. 1. 0.]]

除此之外，有个升级版的OneHotEncoder，这玩意可以将n_categories转化为一个二进制编码。

enc=preprocessing.OneHotEncoder()
x=[['m','g','17'],['fm','r','22']]
enc.fit(x)
print(enc.transform([['fm','r','17'],['m','g','22']]).toarray())

[[1. 0. 0. 1. 1. 0.]
 [0. 1. 1. 0. 0. 1.]]

---

6️⃣ 离散化

离散化预处理可以将非线性特征引入线性模型中。

K桶离散化

KBinsDiscretizer将特征离散到K个桶中

介绍

分桶是离散化的常用方法，将连续型特征离线化为一系列0/1的离散特征。

当数值特征跨越不同的数量级的时候，模型可能只会对大的特征值敏感，这种情况就可以考虑分桶操作。

分桶操作可以看作是对数值变量的离散化，然后通过二值化进行 one hot 编码。

优点

1️⃣分桶后得到的稀疏向量，内积乘法运算速度更快，计算结果更方便存储。

2️⃣对异常数据有很强的鲁棒性。

X = np.array([[-3.,5.,15],[0.,6.,14],[6.,3.,11]])
est = preprocessing.KBinsDiscretizer(n_bins=[3,2,2],encode='ordinal').fit(X)


print(est.transform(X))

[[0. 1. 1.]
 [1. 1. 1.]
 [2. 0. 0.]]

特征二值化

特征二值化是对数字特征进行于阈值化以获得布尔值的过程。

X = [[1.,-1.,2.],[2.,0.,0.],[0.,1.,-1.]]
binarizer = preprocessing.Binarizer().fit(X)
Y1 = binarizer.transform(X)
print(Y1)
binarizer = preprocessing.Binarizer(threshold=1.1)
Y2 = binarizer.transform(X)
print(Y2)

[[1. 0. 1.]
 [1. 0. 0.]
 [0. 1. 0.]]
[[0. 0. 1.]
 [1. 0. 0.]
 [0. 0. 0.]]

---