数据挖掘——1 数据预处理
文章目录
- 一、Data Ceansing 数据清洗
-
- 1.1 为何要进行数据清洗?
- 1.2 缺失值
- 1.3 离群点
- 1.4 重复数据
- 二、Data Transformation 数据转变换
-
- 2.1 为什么要进行数据变换
- 2.2 数据类型
- 2.3 采样
- 三、Data Description 数据描述与可视化
-
- 3.1 数据归一化
- 3.2 经典统计量
- 3.3 数据间的相关性
-
- 3.3.1 相关系数
- 3.3.2 卡方检验
- 3.4 数据可视化
- 四、Feature Selection 特征选择
-
- 4.1 如何进行特征选择
- 五、Feature Extraction 特征提取
- 总结
一、Data Ceansing 数据清洗
1.1 为何要进行数据清洗?
- 数据残缺 例如缺失值
- 噪声 例如在薪水特征下值为-100
- 不一致数据 例如年龄与出身日期不匹配
- 多余数据 即过多的特征或无用数据
- 其他 数据类型不匹配 不平衡数据集
1.2 缺失值
缺失值具有多种类型,比如随机缺失(门店的计数器因为断电断网等原因在某个时段数据为空),数据是否缺失取决于另外一个属性(比如一些女生不愿意填写自己的体重),非随机缺失(比如高收入的人可能不愿意填写收入)。
处理方法:
- 最简单、最直接的方法——删除
- 人工填补缺失值,工作量极大,不可行
- 通过插值等方法自动填补缺失值,常用
插值填补缺失值的方法:
- 均值插补
如果样本属性的距离是可度量的,则使用该属性有效值的平均值来插补缺失的值;
如果的距离是不可度量的,则使用该属性有效值的众数来插补缺失的值。 - 同类均值插补
首先将样本进行分类,然后以该类中样本的均值来插补缺失值。
1.3 离群点
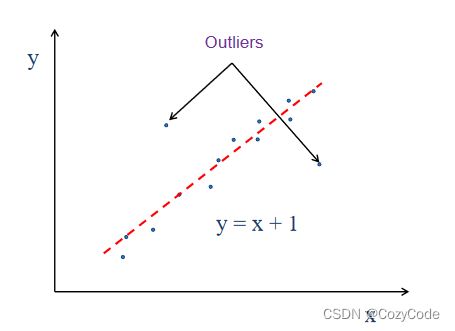
如图所示,有两个离群点,此时如果使用最小二乘法等对其十分敏感的算法,会导致结果偏离严重。
离群点是远离数据集中其余部分的数据,这部分数据可能由随机因素产生,也可能是由不同机制产生。如何处理取决于离群点的产生原因以及应用目的。若是由随机因素产生,我们忽略或者剔除离群点,若是由不同机制产生,离群点就是宝贝,是应用的重点。后者的一个应用为异常行为检测,如在银行的信用卡诈骗识别中,通过对大量的信用卡用户信息和消费行为进行向量化建模和聚类,发现聚类中远离大量样本的点显得非常可疑,因为他们和一般的信用卡用户特性不同,他们的消费行为和一般的信用卡消费行为也相去甚远。还有购物网站检测恶意刷单等场景也重点对离群点进行分析。
1.4 重复数据

如果高度重复或相似的数据距离较近,可以用滑动窗口对比(如上图),然后删除重复值。
为了使得相似记录相邻,可以每条记录生成一个hash key, 根据key去排序,如下图所示。

二、Data Transformation 数据转变换
2.1 为什么要进行数据变换
- 数据需要标准化
- 数据需要进行类型转变
- 数据需要正态化
- 数据需要采样
2.2 数据类型
我们要知道数据主要有以下几种存在形式,并不是所有类型都可以被计算机处理:
- 连续型:具有实数值,例如温度,高度,体重
- 离散型:具有整数值,例如人口数量
- 定序型:具有一定的次序,例如{一般,好,非常好},{低,中,高}
- 定类型:属于同一类,能够列出名字的,{老师,工人,售货员},{红,绿,蓝}
- 字符串:文本数据
2.3 采样
CPU处理数据非常快,但是将数据从硬盘传输到设备上的速度受限,若数据量太大,会消耗非常多的时间,需要对原始数据进行采样。
采样是从特定的概率分布中抽取样本点的过程。采样在机器学习中有非常重要的应用:将复杂分布简化为离散的样本点;用重采样可以对样本集进行调整以更好地进行调整并适应后期的模型学习;用于随机模拟以进行复杂模型的近似求解或推理。采样的一个重要作用是处理不均衡数据集。
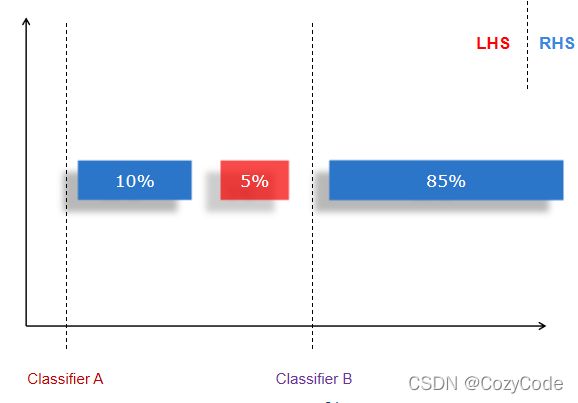
在此数据集中红色只占5%,若使用A划分,会导致模型训练失败,完全无法对A和B进行分类,因为红色样本相对于蓝色样本实在太少了,因此应该在中部进行截取。
对于上图,若直接使用全部数据集进行训练,得到的结果对于蓝色样本的分类结果准确率可能为100%,如果仅仅以分类准确率为判断模型优劣的指标,会与事实违背,因此需要使用新的指标例如:
G mean = ( A c c + × A c c − ) 1 / 2 G_{\text { mean }}=\left(Acc^{+} \times A c c^{-}\right)^{1 / 2} G mean =(Acc+×Acc−)1/2
其中, A c c + = T P T P + F N ; A c c − = T N T N + F P A c c^{+}=\dfrac{T P}{T P+F N} ; \quad A c c^{-}=\dfrac{T N}{T N+F P} Acc+=TP+FNTP;Acc−=TN+FPTN,或者
F measure = 2 × Precision × Recall Precision + Recall F_{\text { measure }}=\frac{2 \times \text { Precision } \times \text { Recall }}{\text { Precision }+\text { Recall }} F measure = Precision + Recall 2× Precision × Recall
其中,Precision = T P T P + F P ; =\dfrac{T P}{T P+F P} ; \quad =TP+FPTP; Recall = T P T P + F N = A c c + =\dfrac{T P}{T P+F N}=A c c^{+} =TP+FNTP=Acc+
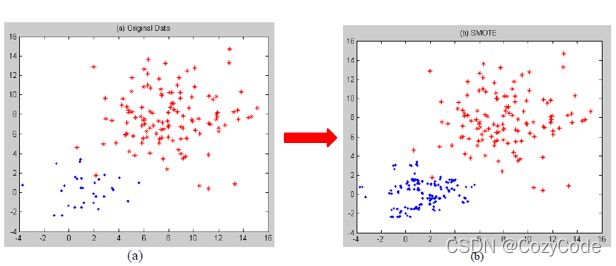
上图所示为过采样,原数据集中蓝色样本点过少,通过插值或者复制等方法增加其数量以提高最终准确率。
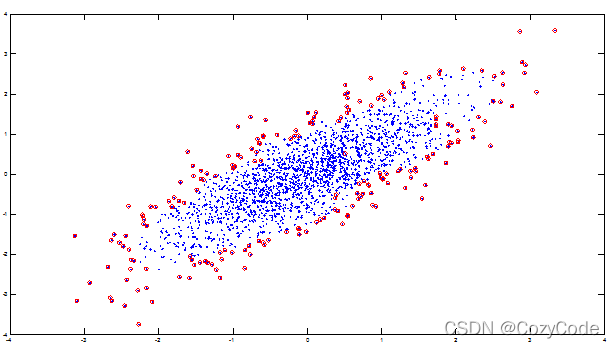
上图为边界采样,原数据集中样本数量过多,假设有几百万条,则在模型进行训练时可能跑一两天也跑不出来,如果对原数据集进行便捷采样,即只取其边界上分布的关键样本点,可能训练结果会有跟原数据集一样好的效果,却可以大大缩短时间。
三、Data Description 数据描述与可视化
3.1 数据归一化
不同的特征具有不同的单位,例如身高1.7米,体重60kg,如果不对其进行归一化而直接使用会导致体重权重过大。
- max-min 最大最小值归一化,需要已知上下界。
v ′ = v − min max − min ( n e w − max − n e w − min ) + n e w − min v^{\prime}=\frac{v-\min }{\max -\min }\left(n e w_{-} \max -n e w_{-} \min \right)+n e w_{-} \min v′=max−minv−min(new−max−new−min)+new−min - Z-score归一化,基于概率分布。
v ′ = v − μ σ v^{\prime}=\frac{v-\mu}{\sigma} v′=σv−μ
其中 μ \mu μ为均值, σ \sigma σ为标准差。
3.2 经典统计量
- 均值
算数平均: x ˉ = 1 n ∑ i = 1 n x i = 1 n ( x 1 + … + x n ) \bar{x}=\frac{1}{n} \sum_{i=1}^{n} x_{i}=\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right) xˉ=n1∑i=1nxi=n1(x1+…+xn)
缺点:易受几个特别大或特别小的值得影响,比如我和马云的平均收入。 - 中位数
P ( X ≤ m ) = P ( X ≥ m ) = ∫ − ∞ m f ( x ) d x = 1 2 P(X \leq m)=P(X \geq m)=\int_{-\infty}^{m} f(x) d x=\frac{1}{2} P(X≤m)=P(X≥m)=∫−∞mf(x)dx=21 - 出现频率最高的元素(mode)
- 方差
用于判断数据间的多样性程度
Var ( X ) = E [ ( X − μ ) 2 ] Var ( X ) = ∫ ( x − μ ) 2 f ( x ) d x \operatorname{Var}(X)=E\left[(X-\mu)^{2}\right] \quad \operatorname{Var}(X)=\int(x-\mu)^{2} f(x) d x Var(X)=E[(X−μ)2]Var(X)=∫(x−μ)2f(x)dx
3.3 数据间的相关性
3.3.1 相关系数
r A , B = ∑ ( A − A ˉ ) ( B − B ˉ ) ( n − 1 ) σ A σ B = ∑ ( A B ) − n A ˉ B ˉ ( n − 1 ) σ A σ B r_{A, B}=\frac{\sum(A-\bar{A})(B-\bar{B})}{(n-1) \sigma_{A} \sigma_{B}}=\frac{\sum(A B)-n \bar{A} \bar{B}}{(n-1) \sigma_{A} \sigma_{B}} rA,B=(n−1)σAσB∑(A−Aˉ)(B−Bˉ)=(n−1)σAσB∑(AB)−nAˉBˉ
- r A , B > 0 r_{A, B}>0 rA,B>0,A和B成正相关
- r A , B = 0 r_{A, B}=0 rA,B=0,A和B不成线性相关(不是不相关)
- r A , B < 0 r_{A, B}<0 rA,B<0,A和B成负相关
3.3.2 卡方检验
χ 2 = ∑ ( Observed − Expected ) 2 Expected \chi^{2}=\sum \frac{(\text { Observed }-\text { Expected })^{2}}{\text { Expected }} χ2=∑ Expected ( Observed − Expected )2
| 下象棋 | 不下象棋 | 总和 | |
|---|---|---|---|
| 喜欢科幻小说 | 250(90) | 200(360) | 450 |
| 不喜欢科幻小说 | 50(90) | 1000(360) | 1050 |
| 喜欢科幻小说 | 300 | 1200 | 1500 |
χ 2 = ( 250 − 90 ) 2 90 + ( 50 − 210 ) 2 210 + ( 200 − 360 ) 2 360 + ( 1000 − 840 ) 2 840 = 507.93 \chi^{2}=\frac{(250-90)^{2}}{90}+\frac{(50-210)^{2}}{210}+\frac{(200-360)^{2}}{360}+\frac{(1000-840)^{2}}{840}=507.93 χ2=90(250−90)2+210(50−210)2+360(200−360)2+840(1000−840)2=507.93
3.4 数据可视化
数据处理一定要能够让人理解,帮助人们思考数据中具有哪些模式,可视化十分重要。

一维数据可用以上方法。

二维数据
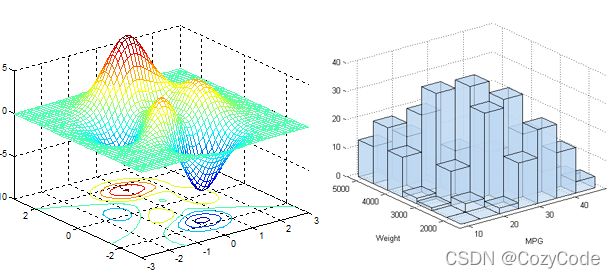
三维数据

高维数据之箱线图
优点:能够直观地看出数据在不同维度的分布。
缺点:看不见数据在各个纬度间的关系,纬度间割裂开。

高维数据之平行坐标图
每个样本点用一条折线表示。
缺点:数据太多时,很难看清。
可视化软件:
- CiteSpace 文献(文本)可视化
- Gephi 网络图关系展示
四、Feature Selection 特征选择
4.1 如何进行特征选择
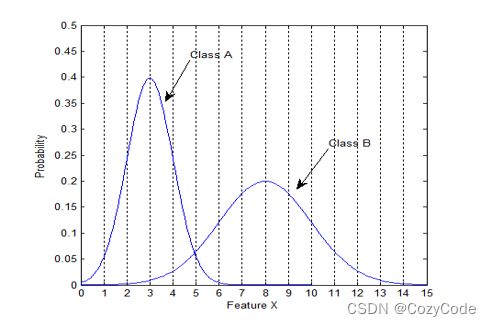
如上图所示,横坐标是特征x,理论上,一个好的特征要能够将两个类别区分开,实际应用中多少会有重合部分。
熵的定义为:
H ( X ) = − ∑ i = 1 n p ( x i ) log b p ( x i ) H(X)=-\sum_{i=1}^{n} p\left(x_{i}\right) \log _{b} p\left(x_{i}\right) H(X)=−i=1∑np(xi)logbp(xi)
熵越小,信息的纯度越高,信息增益越大,得到的信息纯度提升越大。
分支定界法、贪心算法、模拟退火算法、禁忌搜索、遗传算法可用于属性选择。
五、Feature Extraction 特征提取

沿着某一个属性的方差越大,说明这个属性越重要,
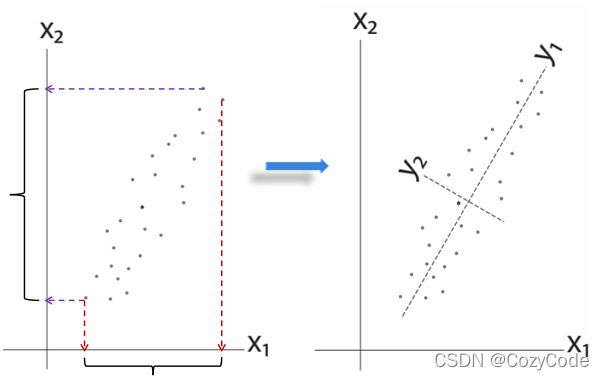
原本具有相关性的两个特征,对其进行去中心化和做变换得到:
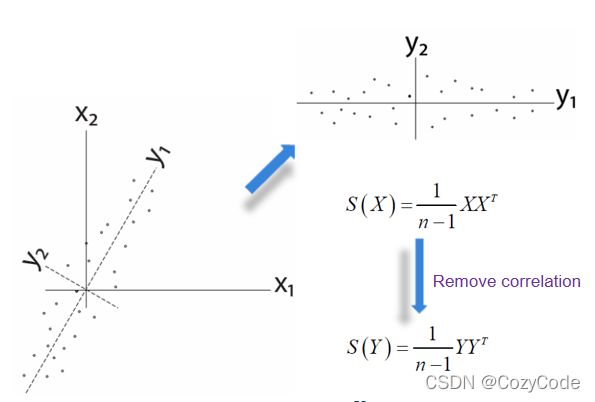
两个特征就变成不相关的了,很明显可以看出y1的方差大于y2。
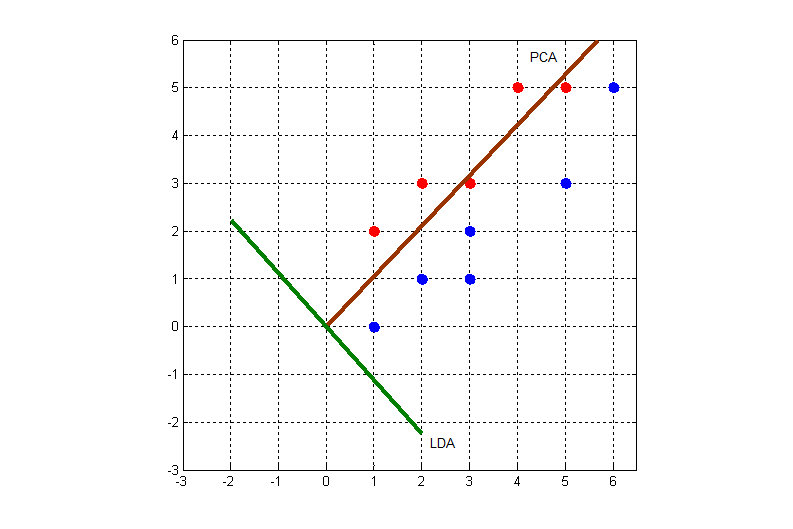
使用主成分分析法进行特征选择,选出特征值最大的几个特征向量。
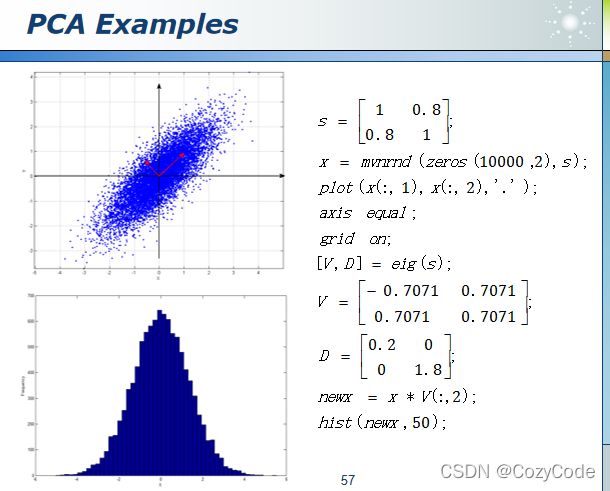
上图为使用MATLAB求PCA。
但是分类问题无法用PCA,PCA为无监督学习,不考虑任何标签,得到的结果无法处理。
有标签数据需要使用线性判别分析LDA。LDA在降维时能够保留类的区分信息。如下图所示,数据经过LDA后得以分开。
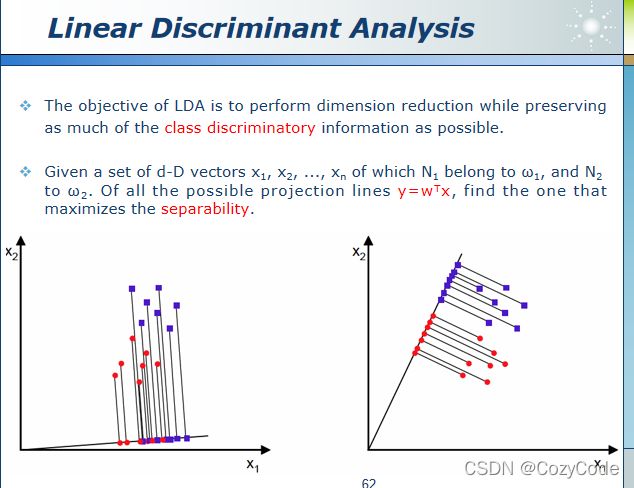
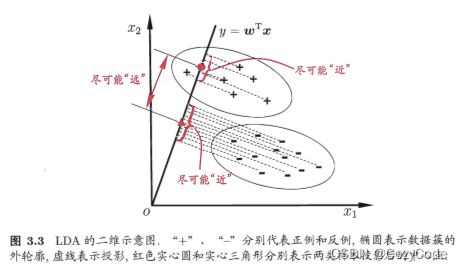
西瓜书中的线性判别分析。
使用LDA降维:


得到结果:
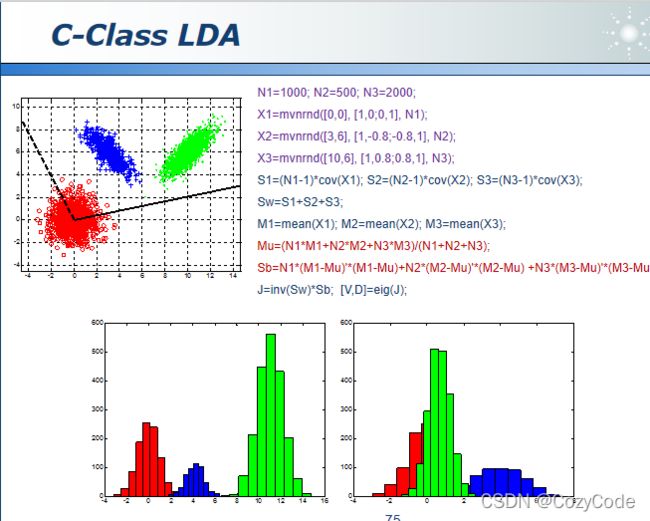
三维LDA同样可以实现,三维LDA可以映射在两个纬度上,即有两个特征向量的特征值不为0,但得到的特征向量不正交。
LDA的限制:
- PCA想降到几维就降到几维,但LDA有维数限制,有C类则C-1维
- 若样本点个数小于纬度,则 S w S_w Sw为奇异阵,不存在逆无法进行LDA计算。 则需要先用PCA降维再用LDA。

此种情况无法进行,两类均值相等。
总结
本文汇总了一些数据预处理的基本原理,后续会继续补充完善,并给出代码实现。