深度学习 神经网络（4）线性回归-Pytorch实现房价预测

一、前言

波士顿房价预测是神经网络线性回归的一个典型应用案例。

本文使用pytorch来的两种方式实现。一种是原生运算思想的矩阵运算，便于理解底层实现；一种是高度封装的更加方便的Sequential方式。

二、Pytorch原生算法实现

2.1 导入并查看数据

from sklearn import datasets  # 导入库
import pandas as pd
import warnings

#忽略warning
warnings.filterwarnings('ignore')

dataset = datasets.load_boston()  # 导入波士顿房价数据
# print(dataset.keys())  # 查看键(属性)     ['data','target','feature_names','DESCR', 'filename'] 
# print(boston.data.shape,boston.target.shape)  # 查看数据的形状 (506, 13) (506,)
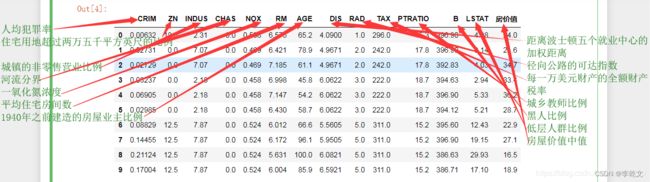
# print(dataset.feature_names)  # 查看有哪些特征 这里共13种
# print(boston.DESCR)  # described 描述这个数据集的信息 
# print(boston.filename)  # 文件路径

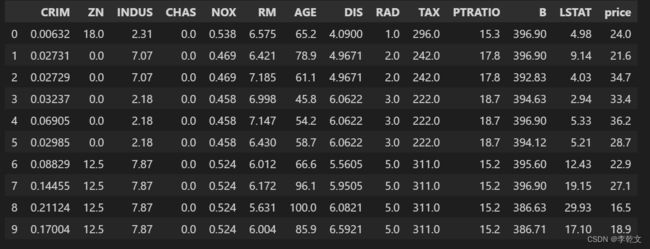
data_df = pd.DataFrame(dataset.data, columns=dataset.feature_names)

data_df['price'] = dataset.target
data_df.head(10)

下图是各特征说明(来自网络)：

2.2 数据预处理

2.2.1 数据归一化

from sklearn.preprocessing import MinMaxScaler
X=dataset.data
Y=dataset.target

#数据归一化
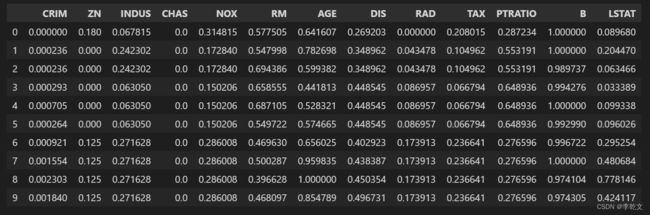
X=MinMaxScaler().fit_transform(X)
data_df = pd.DataFrame(X, columns=dataset.feature_names)
data_df.head(10)

归一化之后的数据：

2.2.2 数据分割

from sklearn.model_selection import train_test_split
# 将数据分割为训练和验证数据，都有特征和预测目标值
# 分割基于随机数生成器。为random_state参数提供一个数值可以保证每次得到相同的分割
X_train, X_test, y_train, y_test = train_test_split(X, Y, random_state = 0)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)

(379, 13) (127, 13) (379,) (127,)

2.3 迭代训练

import torch

#将训练数据转化成tensor格式
x=torch.tensor(X_train,dtype=torch.float32).T
y=torch.tensor(y_train,dtype=torch.float32)

#x、y都是torch.float64类型，权重要保持数据类型一致
weight1=torch.randn((10,13),requires_grad=True)
weight2=torch.randn((1,10),requires_grad=True)

#迭代次数
epochs=1000

#学习率
learning_rate=0.01

plt_epoch=[]
plt_loss=[]

for epoch in range(epochs):
    #计算隐藏层
    hidden=weight1.mm(x)

    #加入激活函数
    hidden=torch.relu(hidden)

    #预测结果
    predictions=weight2.mm(hidden)

    #损失函数
    loss=torch.mean((predictions-y)**2)

    plt_epoch.append(epoch)
    plt_loss.append(loss.item())

    #打印损失值
    if epoch%100==0:
        print('epoch:',epoch,'loss:',loss.item())

    #反向传播
    loss.backward()

    #更新权重
    weight1.data-=weight1.grad*learning_rate
    weight2.data-=weight2.grad*learning_rate

    #记得清空梯度，不然会一直累加
    weight1.grad.zero_()
    weight2.grad.zero_()

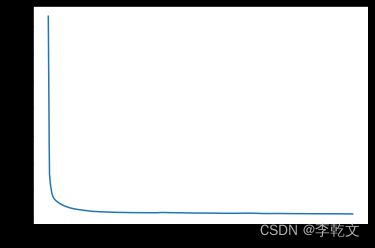
#绘制迭代次数与损失函数的关系
import matplotlib.pyplot as plt
plt.plot(plt_epoch,plt_loss)

epoch: 0 loss: 736.4046630859375
epoch: 100 loss: 28.843740463256836
epoch: 200 loss: 19.532974243164062
epoch: 300 loss: 17.543787002563477
epoch: 400 loss: 17.788957595825195
epoch: 500 loss: 16.18192481994629
epoch: 600 loss: 15.367783546447754
epoch: 700 loss: 14.757761001586914
epoch: 800 loss: 14.272703170776367
epoch: 900 loss: 13.704763412475586

2.4 数据验证

#测试数据
x_t=torch.tensor(X_test,dtype=torch.float32).T
y_t=torch.tensor(y_test,dtype=torch.float32)

#计算隐藏层
hidden=weight1.mm(x_t)

#加入激活函数
hidden=torch.relu(hidden)

#预测结果
predictions=weight2.mm(hidden)

#损失函数
loss=torch.mean((predictions-y_t)**2)
print('loss:',loss.detach().item())

28.643226623535156

三、Sequential简化代码实现

from sklearn import datasets
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
import torch
import torch.nn as nn

import warnings
#忽略warning
warnings.filterwarnings('ignore')


torch.manual_seed(0)

#加载数据集
X,Y = datasets.load_boston(return_X_y=True)

#数据归一化
X=MinMaxScaler().fit_transform(X)

#数据分割
X_train, X_test, y_train, y_test = train_test_split(X, Y, random_state = 0)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)

#将训练数据转化成tensor格式
x=torch.tensor(X_train,dtype=torch.float32)
y=torch.tensor(y_train,dtype=torch.float32)

#迭代次数
epochs=1000

#学习率
learning_rate=0.01

plt_epoch=[]
plt_loss=[]

#定义神经网络各层结构和激活函数
model = nn.Sequential(
    nn.Linear(x.size()[1], 10),
    nn.ReLU(),
    # nn.Linear(10, 10),
    # nn.ReLU(),
    nn.Linear(10, 1)
)

#损失函数
cost=nn.MSELoss()
#迭代优化器
optmizer=torch.optim.SGD(model.parameters(),lr=learning_rate)

for epoch in range(epochs):
    #预测结果
    predictions=model(x) #调用__call__函数

    #计算损失值
    loss=cost(predictions,y)

    #在反向传播前先把梯度清零
    optmizer.zero_grad()

    #反向传播,计算各参数对于损失loss的梯度
    loss.backward()

    #根据刚刚反向传播得到的梯度更新模型参数
    optmizer.step()

    plt_epoch.append(epoch)
    plt_loss.append(loss.item())

    #打印损失值
    if epoch%100==0:
        print('epoch:',epoch,'loss:',loss.item())


#绘制迭代次数与损失函数的关系
import matplotlib.pyplot as plt
plt.plot(plt_epoch,plt_loss)

(379, 13) (127, 13) (379,) (127,)
epoch: 0 loss: 612.2507934570312
epoch: 100 loss: 86.63423156738281
epoch: 200 loss: 86.0482406616211
epoch: 300 loss: 85.77094268798828
epoch: 400 loss: 85.62319946289062
epoch: 500 loss: 85.53376007080078
epoch: 600 loss: 85.474365234375
epoch: 700 loss: 85.431640625
epoch: 800 loss: 85.39983367919922
epoch: 900 loss: 85.37591552734375

#测试数据
x_t=torch.tensor(X_test,dtype=torch.float32)
y_t=torch.tensor(y_test,dtype=torch.float32)

#预测结果
predictions=model(x_t)
#计算损失值
loss=cost(predictions,y_t)

print('loss:',loss.detach().item())

loss: 81.83320617675781