传统机器学习笔记6——回归树模型
目录
- 前言
- 一.决策树回归
-
- 1.1.核心思想
- 二.启发式切分与最优属性选择
-
- 2.1.回归模型示例
- 2.2.回归树的构建方法
- 递归二分
- 过拟合与正则化
-
- 3.1.过拟合问题
- 3.2.过拟合问题的解决方法
-
- 3.2.1.约束控制树的过度生长
- 3.2.2.剪枝
- 3.2.3.正则化
前言
我们在前面部分介绍了决策树分类模型,有不了解的小伙伴可以回到前面学习一下,传统机器学习笔记4——决策树。实际上决策树也可以用作回归任务,我们称之为回归树,核心还是树形结构,只是属性的生长方式和分类的决策树有所不同。
一.决策树回归
1.1.核心思想
我们再来看下决策树的典型结构,如下图所示:关于决策树的更详细的内容介绍可以回到前面看看,这里就不再重复介绍了。
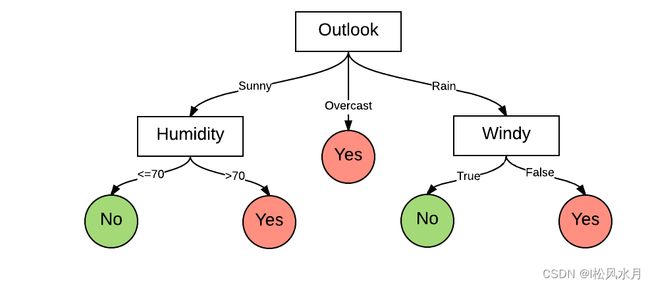
我们先来看下决策树的核心思想,提到回归树,我们首先想到的就是CART树,CART树全称Classification And Regression Trees,即分类树与回归树。CART树有以下特点:
假设决策树是二叉树,内部节点特征的取值为是和否,右分支是取值为是的分支,左分支是取值为否的分支。这样的决策树等价于对每个特征进行递归二分,将输入的空间划分为有限个单元,并在这些单元上确定预测的概率分布,也就是在输入给定的条件下输出条件概率分布。我们先假设有数据集D,构建回归树的大致思路如下:
- 考虑数据集D上的所有特征j,遍历每个特征下的所有可能取值或者切分点s,将数据集D划分成两部分 D 1 , D 2 D_{1},D_{2} D1,D2。
- 分别计算 D 1 , D 2 D_{1},D_{2} D1,D2的平方差和,选择最小的的平方差对应的特征与分割点,生成两个子节点,即将数据划分成两部分。
- 对上述两个子节点递归调用步骤1,2,知道满足停止条件。
回归树构建好以后,就完成了对整体输入空间的划分,也就是完成了对回归树的建立。将整个输入空间划分为多个子区域,每个子区域输出为该区域内所有训练样本的平均值。我们来看两个示例:
将整个输入空间划分为多个子区域:
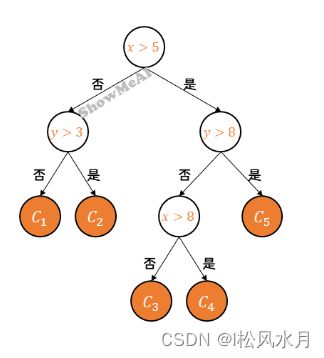
每个子区域输出为该区域内所有训练样本的平均值:
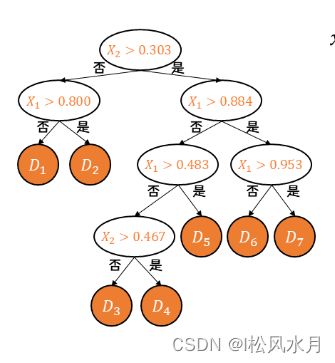
我们知道了回归树其实是将输入空间划分为 个单元,每个区域的输出值是该区域内所有点 值的平均数。但我们希望构建最有效的回归树:预测值与真实值差异度最小。下面我们介绍下回归树是如何生长的。
二.启发式切分与最优属性选择
2.1.回归模型示例
下面我们以棒球运动员的收入为例来解释回归模型,如下图所示:

其中:
- 红黄表示高收入,蓝绿表示低收入
- 横坐标表示年限,纵坐标表示成绩表现
总共有两个特征,从业年限years和成绩表现hits,回归树的决策过程由最终生成的回归树决定,如下图所示:

根决策节点为特征years ,其划分阈值为 4.5, years小于4.5的样本划分到左边,大于或等于4.5的样本划分到右边;第二个决策节点的特征为hits ,其划分阈值为117.5,hits小于117.5的样本划分到左边,大于或等于117.5的样本划分到右边。一个样本顺着决策树的决策条件,走到叶子节点,即可获得预测工资,这里的预测工资总共就3种取值,分别为5.11 、6.0、6.74。
回归树构建完成后,实现了对整个空间的划分,如下图所示。实际预测时,新样本会按照回归树的决策过程,被划分到下图 R 1 R_{1} R1、 R 1 R_{1} R1、 R 1 R_{1} R1之中的一个区域 R i R_{i} Ri,而这个新样本的预测值(本案例中为棒球运动员的工资)就是它所在的区域。如下图所示,整个平面被分为3部分:
R 1 = X ∣ Years < 4.5 R 2 = X ∣ Years ≥ 4.5 , Hits < 117.5 R 3 = X ∣ Years ≥ 4.5 , Hits ≥ 117.5 \begin{gathered} R 1=X \mid \text { Years }<4.5 \\ R 2=X \mid \text { Years } \geq 4.5, \text { Hits }<117.5 \\ R 3=X \mid \text { Years } \geq 4.5, \text { Hits } \geq 117.5 \end{gathered} R1=X∣ Years <4.5R2=X∣ Years ≥4.5, Hits <117.5R3=X∣ Years ≥4.5, Hits ≥117.5

2.2.回归树的构建方法
构建回归树的核心:切分方式与属性选择先假设一个回归问题,预估结果为 y ∈ R y \in R y∈R ,特征向量为 X = [ x 1 , x 2 , x 3 , … , x p ] X=\left[x_1, x_2, x_3, \ldots, x_p\right] X=[x1,x2,x3,…,xp] ,那么构建回归树的2个步骤为:
- 先把特征空间X切分成J个没有重叠的区域 X = [ R 1 , R 2 , R 3 , … , R p ] X=\left[R_1,R_2, R_3, \ldots, R_p\right] X=[R1,R2,R3,…,Rp]
- 其中 R J R_{J} RJ中的每个样本我们都给一样的预测结果 y ~ R j = 1 n ∑ j ∈ R j y j \tilde{y}_{R_{j}}=\frac{1}{n} \sum j \in R j y_j y~Rj=n1∑j∈Rjyj,其中n是 R J R_{J} RJ中样本的总数。
通过上面的构建,我们希望找到一个使RSS最小的划分方式 R 1 , R 2 , R 3 , . . . R J R_{1},R_{2},R_{3},...R_{J} R1,R2,R3,...RJ,RSS表示如下:
R S S = ∑ j = 1 J ∑ i ∈ R j ( y i − y ~ R j ) 2 R S S=\sum_{j=1}^J \sum_{i \in R j}\left(y_i-\tilde{y}_{R_j}\right)^2 RSS=j=1∑Ji∈Rj∑(yi−y~Rj)2
其中:
- y y y :为每个训练样本的标签构成的标签向量,向量中的每个元素 y j y_j yj 对应的是每个样本的标签。
- X X X :为特征的集合, x 1 , x 2 , … , x p x_1, x_2, \ldots, x_p x1,x2,…,xp 为第 1 个特征到第 p p p 个特征。
- R 1 , R 2 , R 3 , … , R J R_1, R_2, R_3, \ldots, R_J R1,R2,R3,…,RJ :为整个特征空间划分得来的个个不重叠的区域 (可以参考上页的右图)。
- y ~ R j \tilde{y}_{R_j} y~Rj:为划分到第 j j j 个区域 R j R_j Rj 的样本的平均标签值,用这个值作为该区域的预测值,即如果有一个测试样 本在测试时落入到该区域,就将该样本的标签值预测为
y ~ R j \tilde{y}_{R_j} y~Rj 。
从上面的计算过程可以看到,当特征空间比较复杂的时候,计算量是非常大的。于是就引出了下面我们要介绍的递归二分法。
递归二分
回归树采用的是一种自顶向下的贪婪式递归方式。这里的贪婪,指的是每一次的划分,只考虑当前最优,而不回头考虑之前的划分。从数学上定义,即选择切分的维度(特征) 以及切分点 使得划分后的树RSS结果最小,公式如下所示:
R 1 ( j , s ) = { x ∣ x j < s } R 2 ( j , s ) = { x ∣ x j ≥ s } R S S = ∑ x i ∈ R 1 ( j , s ) ( y i − y ~ R 1 ) 2 + ∑ x i ∈ R 2 ( j , s ) ( y i − y ~ R 2 ) 2 \begin{aligned} &R_1(j, s)=\left\{x \mid x_j
我们再来看下递归切分,直接看下面的两张图,左图是非递归切分得到的,右图是二分递归方式。
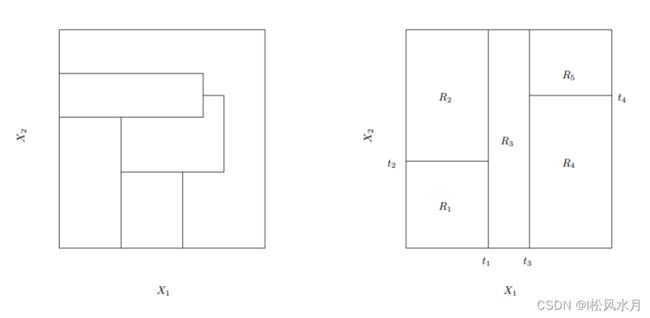
从上面的图可以看到,递归切分一定可以找到一个较优的解,非递归切分穷举不了所有情况,算法上无法实现,可能无法得到一个较好的解。
回归树总体流程类似于分类树:分枝时穷举每一个特征可能的划分阈值,来寻找最优切分特征和最优切分点阈值,衡量的方法是平方误差最小化。分枝直到达到预设的终止条件(如叶子个数上限)就停止。
通常在处理具体问题时,单一的回归树模型能力有限且有可能陷入过拟合,我们经常会利用集成学习中的Boosting思想,对回归树进行增强,得到的新模型就是提升树(Boosting Decision Tree),进一步,可以得到梯度提升树(Gradient Boosting Decision Tree,GBDT),再进一步可以升级到XGBoost。通过多棵回归树拟合残差,不断减小预测值与标签值的偏差,从而达到精准预测的目的。
过拟合与正则化
3.1.过拟合问题
当树的规模太小会导致模型效果不佳,而树的规模太大就会造成过拟合,非常难以控制,因此就诞生了以下几种解决过拟合的方法。
3.2.过拟合问题的解决方法
3.2.1.约束控制树的过度生长
- 限制树的深度:当达到设置的最大深度时结束树的生长。
- 分类误差法:当树继续生长无法得到希望的分类误差减小,就停止生长。
- 叶子节点最小数据量限制:一个叶子节点的数据量过小,树停止生长。
3.2.2.剪枝
约束树生长的缺点就是提前扼杀了其他可能性,过早地终止了树的生长,我们也可以等待树生长完成以后再进行剪枝,即所谓的后剪枝,而后剪枝算法主要有以下几种:
- Reduced-Error Pruning(REP,错误率降低剪枝)。
- Pesimistic-Error Pruning(PEP,悲观错误剪枝)。
- Cost-Complexity Pruning(CCP,代价复杂度剪枝)。
- Error-Based Pruning(EBP,基于错误的剪枝)。
3.2.3.正则化
对于回归树而言,在剪枝过程中我们会添加正则化项衡量。如下所示,考虑剪枝后得到的子树 ,其中 是正则化项的系数。当固定住 之后,最佳的 就是使得下列式子值最小的子树。
∑ m = 1 ∣ T ∣ ∑ x i ∈ R m ( y i − y ~ R 2 ) 2 + α ∣ T ∣ \sum_{m=1}^{|T|} \sum_{x_i \in R_m}\left(y_i-\tilde{y}_{R_2}\right)^2+\alpha|T| m=1∑∣T∣xi∈Rm∑(yi−y~R2)2+α∣T∣
- ∣ T ∣ |T| ∣T∣是回归树叶子节点的个数。
- α \alpha α可以通过交叉验证去选择。
关于回归树的模型原理部分基本上介绍完了,欢迎各位大佬批评指正。