传统机器学习笔记7——GBDT模型详解
目录
- 前言
- 一.GBDT算法
-
- 1.1.Boosting
- 1.2.GDBT
-
- 1.2.1.GBDT与负梯度近似残差
- 1.2.2.GDBT训练过程
- 二.梯度提升与梯度下降
- 三.GDBT模型优缺点
- 四.GDBT vs 随机森林
前言
上篇博文我们介绍了关于回归树模型的基本知识点,有不懂的小伙伴可以回到前面再看下,传统机器学习笔记6——回归树模型。这篇博文我们继续介绍传统机器学习的内容,传统机器学习之GBDT。
一.GBDT算法
GBDT(Gradient Boosting Decision Tree),即梯度提升决策树,是一种迭代的决策树算法,我们又称为MART,他通过构造一组弱的学习器,并把多颗决策树的结果累加起来最为最终的预测结果,将决策树与集成算法进行了有效的结合。
1.1.Boosting
在介绍GDBT算法之前,我们还需要先看下Boosting。Boosting方法训练及分类器的时候采用串行的方式,各个基分类器之间有依赖,他的思路就是将基分类器进行层层叠加,每一层训练的时候对前一层基分类器分错的样本给予更高的权重,测试的时候根据各层分类器的结果的加权得到最终的结果。注意这里跟我们之前介绍的Bagging,Bagging在训练的时候,各个基分类器之间无强依赖,可以进行并行训练。关于Bagging有不懂的小伙伴可以回到前面的博文回顾下,1.4.Bagging。
1.2.GDBT
下面我们开始正式介绍GDBT算法,其实他的原理很简单原理如下:
- 所有弱分类器的结果相加等于预测值。
- 每次都以当前预测为基准,下一个弱分类器去拟合误差函数对预测值的残差(预测值与真实值之间的误差)。
- GBDT的弱分类器使用的是树模型。
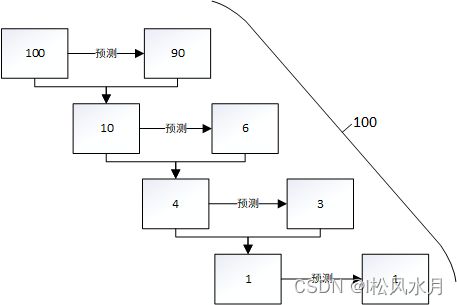
- 第一个弱分类器(第一棵树)预测一个年龄(如90元),计算发现误差有10元;
- 第二棵树预测拟合残差,预测值6元,计算发现差距还有4元;
- 第三棵树继续预测拟合残差,预测值3元,发现差距只有公式1元;
- 第四课树用1元拟合剩下的残差,完成。
最终,四棵树的结论加起来,得到100元这个标注答案(实际工程实现里,GBDT 是计算负梯度,用负梯度近似残差)。
1.2.1.GBDT与负梯度近似残差
在做回归任务时,GDBT在每一轮的迭代时都会对样本有个预测值,此时的损失函数为均方误差损失函数:
l ( y i , y ^ i ) = 1 2 ( y i − y ^ i ) 2 l\left(y_i, \hat{y}_i\right)=\frac{1}{2}\left(y_i-\hat{y}_i\right)^2 l(yi,y^i)=21(yi−y^i)2
损失函数的负梯度计算
− [ ∂ l ( y i , y i ^ ) ∂ y ^ i ] = ( y i − y i ^ ) -\left[\frac{\partial l\left(y_i, \hat{y_i}\right)}{\partial \hat{y}_i}\right]=\left(y_i-\hat{y_i}\right) −[∂y^i∂l(yi,yi^)]=(yi−yi^)
从上面的公式可以看出,当损失函数为均方误差时,每一次的拟合的值就是“真实值-预测值”,即残差。
1.2.2.GDBT训练过程
我们下面以预测四个人的年龄为例来介绍下GDBT的训练过程。假设现在有四个人(A,B,C,D),他们的年龄分别是(14,16,24,26)。其中A,B为高一,高二学生,C,D为应届生和工作两年的员工,我们先用回归树来训练,有如下结果:

接下来我们使用GBDT来做这件事,由于数据太少,我们限定叶子节点最多有两个,即每棵树都只有一个分枝,并且限定只学两棵树。我们会得到如下图2所示结果:

上图中的左图和上面的决策树图一样,由于A,B年龄较为相近,C,D年龄较为相近,他们被分为两拨,每拨用平均年龄作为预测值。此时计算残差(即 A的预测值 + A的残差 = A的实际值),所以A的残差就是16-15=1(注意,A的预测值是指前面所有树累加的和,这里前面只有一棵树所以直接是15,如果还有树则需要都累加起来作为A的预测值)。进而得到A,B,C,D的残差分别为-1,1,-1,1。然后我们拿残差替代A,B,C,D的原值,到第二棵树去学习,如果我们的预测值和它们的残差相等,则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了。这里的数据显然是我可以做的,第二棵树只有两个值1和-1,直接分成两个节点。此时所有人的残差都是0,即每个人都得到了真实的预测值。也就是说,现在A,B,C,D的预测值都和真实年龄一致了。
- A: 14岁高一学生,购物较少,经常百度提问;预测年龄A = 15 – 1 = 14
- B: 16岁高三学生;购物较少,经常回答问题;预测年龄B = 15 + 1 = 16
- C: 24岁应届毕业生;购物较多,经常百度问题;预测年龄C = 25 – 1 = 24
- D: 26岁工作两年员工;购物较多,经常回答问题;预测年龄D = 25 + 1 = 26
二.梯度提升与梯度下降
下面我们再来对比下梯度提升和梯度下降算法,两种迭代优化算法,都是在每1轮迭代中,利用损失函数负梯度方向的信息,更新当前模型。我们先来看下两种模型的计算公式。
梯度下降:
梯度下降中,模型是以参数化形式表示,从而模型的更新等价于参数的更新。
F = F t − 1 − ρ t ∇ F L ∣ F = F t − 1 L = ∑ i l ( y i , F ( x i ) ) \begin{gathered} F=F_{t-1}-\left.\rho_t \nabla_F L\right|_{F=F_{t-1}} \\ L=\sum_i l\left(y_i, F\left(x_i\right)\right) \end{gathered} F=Ft−1−ρt∇FL∣F=Ft−1L=i∑l(yi,F(xi))
梯度上升:
梯度提升中,模型并不需要进行参数化表示,而是直接定义在函数空间中,从而大大扩展了可以使用的模型种类。
w t = w t − 1 − ρ t ∇ w L ∣ w = w t − 1 L = ∑ i l ( y i , f w ( w i ) ) \begin{gathered} w_t=w_{t-1}-\left.\rho_t \nabla_w L\right|_{w=w_{t-1}} \\ L=\sum_i l\left(y_i, f_w\left(w_i\right)\right) \end{gathered} wt=wt−1−ρt∇wL∣w=wt−1L=i∑l(yi,fw(wi))
三.GDBT模型优缺点
上面我们介绍了GDBT模型的基本算法,那么他有哪些优缺点呢?
优点:
- 预测阶段,因为每棵树的结构都已确定,可并行化计算,计算速度快。
- 适用稠密数据,泛化能力和表达能力都不错,数据科学竞赛榜首常见模型。
- 可解释性不错,鲁棒性亦可,能够自动发现特征间的高阶关系。
缺点:
- GBDT 在高维稀疏的数据集上,效率较差,且效果表现不如 SVM 或神经网络。
- 适合数值型特征,在 NLP 或文本特征上表现弱。
- 训练过程无法并行,工程加速只能体现在单颗树构建过程中。
四.GDBT vs 随机森林
相同点:
- 都是集成模型,由多棵树组构成,最终的结果都是由多棵树一起决定。
- RF 和 GBDT 在使用 CART 树时,可以是分类树或者回归树。
不同点:
- 训练过程中,随机森林的树可以并行生成,而 GBDT 只能串行生成。
- 随机森林的结果是多数表决表决的,而 GBDT 则是多棵树累加之。
- 随机森林对异常值不敏感,而 GBDT 对异常值比较敏感。
- 随机森林降低模型的方差,而 GBDT 是降低模型的偏差。