机器学习实战—决策树算法
文章目录
- 一.简介
- 二.决策树训练和可视化
-
- 2.1 决策树分类算法使用
- 2.2 决策树可视化
- 2.3 决策树预测流程
- 2.4 决策树估计类概率
- 三.CART剪枝训练算法
-
- 3.1 简介
- 3.2 Cart分类成本函数
- 四.基尼不纯度或熵
-
- 4.1 简介
- 4.2 决策树的第i个节点熵的计算公式
- 4.3 正则化参数
- 五. 回归问题
-
- 5.1 决策树回归算法的使用
- 5.2 决策树可视化
- 5.3 Cart回归成本函数
- 六. 总结
一.简介
决策树是一种多功能的机器学习算法,它可以实现分类和回归任务,甚至是多输出任务。它功能强大能够拟合复杂的数据集。决策树同时也是随机森林的基本组成部分,随机森林是现今最强大的机器学习算法之一。
二.决策树训练和可视化
2.1 决策树分类算法使用
决策树是一种树形结构,其中每个结点表示一个属性上的判断(相当于if-else结构),每个分支代表一个判断结果的输出,最后每个叶节点代表一种分类结果,本质是一棵由多个判断节点组成的树。下面利用鸢尾花数据集来看看决策树是如何做出预测的。
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris=load_iris() #加载数据集
X=iris.data[:,2:] #取2-3列的数据
y=iris.target #目标值
tree_clf=DecisionTreeClassifier(max_depth=2)
tree_clf.fit(X,y)
2.2 决策树可视化
决策树的可视化使用export_graphviz()方法输出一个图形定义文件,在使用之前我们要先安装graphviz
conda install graphviz
from sklearn.tree import export_graphviz
export_graphviz(
tree_clf,
out_file="iris_tree.dot",
feature_names=iris.feature_names[2:],
class_names=iris.target_names,
rounded=True,
filled=True
)
下面将dot文件转换为png,查看其内容
%%bash
dot -Tpng iris_tree.dot -o iris_tree.png
samples:统计它应用的训练实例数量
value:说明了该节点上应用在每个类别的训练实例数量
gini:衡量其不纯度,如果应用的所有训练实例都属于同一个类被,那么节点就是纯的(gini=0)基尼不纯度的计算公式如下:
G i = 1 − ∑ k = 1 n p i , k 2 G_i=1-\sum_{k=1}^np_{i,k}^2 Gi=1−k=1∑npi,k2
p i , k 是第 i 个节点中训练实例之间的 k 类实例的比率 p_{i,k}是第i个节点中训练实例之间的k类实例的比率 pi,k是第i个节点中训练实例之间的k类实例的比率
2.3 决策树预测流程
下面看看来了一个新的鸢尾花实例,我们是如何对这个新的实例进行预测的(结合上面的树图)。
- 首先从根节点开始(深度为0,在顶部),该节点判断花瓣长度(petal length)是否小于2.45cm,如果是就进入左下节点,该节点是叶子节点,进入这个节点可以判断这个类别为setosa,如果花瓣长度大于2.45进入右节点。
- 进入右节点后,再判断花瓣宽度(petal width)是否小于1.75cm,如果小于就进入左边节点,则其类为versicolor,否则进入右节点判断其类为virginica
2.4 决策树估计类概率
决策树除了可以像上面鸢尾花案例判断某个实例属于某个类别外,还可以估算某个实例属于特定类k的概率。它的估计方法是,首先跟随决策树找到该实例的叶节点,然后返回该节点中类k的训练实例占比。
三.CART剪枝训练算法
3.1 简介
Scikit-Learn使用分类和回归树(CART)算法来训练决策树,其工作原理是首先使用一个特征k并设定该特征的阈值将数据集分为两个部分(也是树将整个数据集分成了左右两个子树),然后在子树上使用相同的逻辑选取新的特征并设置该新特征的阈值,子树的数据集又被分成了两个部分,以此类推直到达到规定的最大深度时停止分割,很容易发现最后形成的决策树是一个二叉树。那么如何选择特征k以及设定其阈值,这就需要CART分类成本函数来做。
3.2 Cart分类成本函数
J ( k , t k ) = m l e f t m G l e f t + m r i g h t m G r i g h t J(k,t_k)=\frac {m_{left}} m G_{left}+\frac {m_{right}} m G_{right} J(k,tk)=mmleftGleft+mmrightGright
其中 { G l e f t / r i g h t :测量左右子集的不纯度(公式在上) m l e f t / r i g h t :测量左右子集的实例数 其中\begin{cases} G_{left/right}:测量左右子集的不纯度(公式在上)\\ m_{left/right}:测量左右子集的实例数\\ \end{cases} 其中{Gleft/right:测量左右子集的不纯度(公式在上)mleft/right:测量左右子集的实例数
CART是一种贪婪算法,从顶层开始搜索最优分裂,然后迭代这个过程,最后它并不会检查这个分裂的不纯度是否为可能的最低值。贪婪算法通常会产生一个相当不错的解,但不能保证是最优解。
四.基尼不纯度或熵
4.1 简介
前面我们计算不纯度的方法是通过基尼不纯度,不纯度是决策树分类的原理,它分类时会让所分的几个类别内部的不纯度达到最小,除了基尼不纯度来测量不纯度还可以使用熵作为不纯度的测量方式。熵的概念来自于热力学,是一种分子程度的度量。在机器学习中,熵经常被用作一种不纯度的测量方式:如果数据集中仅包含一个类别的实例,其熵为零。
4.2 决策树的第i个节点熵的计算公式
H i = − ∑ k = 1 n P i , k l o g 2 ( p i , k ) H_i=-\sum_{{k=1}}^n P_{i,k}log_2(p_{i,k}) Hi=−k=1∑nPi,klog2(pi,k)
在基尼不纯度和熵之间做出选择时,大多数情况下它们是没什么区别的,产生的树都很相似。基尼不纯度的计算速度略微快一些,它们的不同在于,基尼不纯度倾向于从树枝中分裂出最常见的类别,而熵则倾向于生产更平衡的树。
4.3 正则化参数
决策树基本上不对数据集进行假设(不同于线性模型假设数据是呈线性的),如果不加以限制,树的结构将跟随训练集变化,导致过拟合,决策树解决过拟合有两种方案:
- 为避免过拟合,需要在训练过程中进行正则化,对一些超参数进行限制(比如树的最大深度)
- 可以先不加约束的训练模型,训练完后对决策树进行剪枝操作,删除一些没有必要的节点
五. 回归问题
5.1 决策树回归算法的使用
前面介绍了用决策树解决分类问题,决策树同样可以解决回归问题,使用的API是Scikit-learn的DecisionTreeRegressor类构建一个回归树。
from sklearn.tree import DecisionTreeRegressor
tree_reg=DecisionTreeRegressor(max_depth=2)
tree_reg.fit(X,y)
from sklearn.tree import export_graphviz
export_graphviz(
tree_reg,
out_file="iris_tree2.dot",
feature_names=iris.feature_names[2:],
class_names=iris.target_names,
rounded=True,
filled=True
)
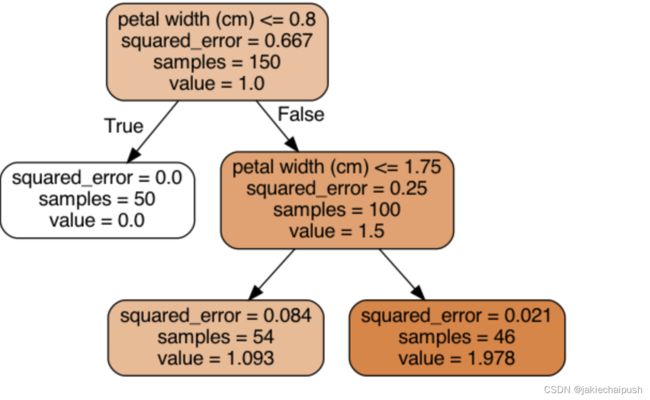
5.2 决策树可视化
- 首先在根节点,判断petal width<=0.8不成立进入右子树
- 然后在右子树的根节点判断petal width<=1.75不成立,进入有子树
- 右子树为叶子节点,预测结束预测值为value=1.978,Mse=0.021
5.3 Cart回归成本函数
CART算法在这里的工作原理和前面介绍分类问题的原理是大致一样的,不同之处它不再尝试以最小化不纯度的方式来拆分训练集,而是以最小化MSE的方式来拆分训练集。Cart回归成本函数如下:
J ( k , t k ) = m l e f t m M S E l e f t + m r i g h t m M S E r i g h t J(k,t_k)=\frac {m_{left}} m MSE_{left}+\frac {m_{right}} m MSE_{right} J(k,tk)=mmleftMSEleft+mmrightMSEright
其中 { M S R l e f t = ∑ ( y ^ l e f t − y i ) y ^ l e f t = ∑ y ( i ) l e f t 的实例总数 其中\begin{cases} MSR_{left}=\sum(\hat y_{left}-y^{i})\\ \hat y_{left}=\frac {\sum y^{(i)}} {left的实例总数}\\ \end{cases} 其中{MSRleft=∑(y^left−yi)y^left=left的实例总数∑y(i)
六. 总结
总的来说决策树易于理解和解释、易于使用、用途广泛且功能强大。但它也有局限性,决策树喜欢正交决策边界(如下图分类中所有的分割都是垂直于轴),这种特性导致了它们对训练集合的旋转时及其敏感的,如下图我们将图左的数据集进行旋转一下已知,决策树的分割似乎复杂了很多。更概括的说,决策树的主要问题是它们对训练数据中的小变化非常敏感。