Python算法:决策树分类
Python算法:决策树分类
文章目录
- Python算法:决策树分类
-
- 一、前言
- 二、决策树算法原理介绍
-
- 1、决策树原理
- 2、决策树构造
- 3、交叉验证
- 三、决策树算法函数介绍
-
- 1、 train_test_split函数
- 2、tree.DecisionTreeClassifier函数
- 四、数据说明
- 五、编写Python决策树程序并运行
- 六、最后我想说
一、前言
作为算法小白的我,现在要开始进行Python算法学习了,因为算法在今后的发展中实在是太重要了,刚好我们学校大数据平台上面有有关Python算法的实验,我打算挨个来学习。
可能有人会说为什么要Python进行算法练习,一般不都是使用C/C++和Java吗,我想说的是,因为我想做数据开发方面的工作,然后本人本身也是大数据专业的,后续考研也会选择有关大数据开发的方向进行深造,而在大数据方面、机器学习方面目前使用最多的语言也就是Python,所以我才进行Python的算法练习。
后续我还想去尝试打kaggle的比赛,那也是后面的事了,目前的我实力太弱了。
好啦,废话不多说,我们开始Python算法练习!
二、决策树算法原理介绍
1、决策树原理
决策树是一种比较常用的分类算法,理解起来也相对容易。所谓决策树分类就是用决策条件构成的一个树状预测模型,通过这个模型,我们可以对未知类别的数据进行分类。下面举一个简单的例子来说明。比如期末班级评选三好学生的时候,大家通过投票来评选自己心目中的优秀学生,你在考虑某位同学是否有资格成为三好学生时,可能会分别考虑他的品德、成绩和体育三个方面,你的决策过程可能如下图所示:
上图表示你在考虑一位同学是否是三好学生时,先考虑他的品德,如果品德不好的话,直接认为他不是一位好学生,如果品德优良的话那再看他的成绩是否足够好,依此类推。图中蓝色的节点表示判断条件,红色表示决策结果,箭头表示在一个判断条件在不同情况下的决策路径。
上面的例子中只是用来说明,与实际的决策树还是有些差别。首先,在决策树中判断条件通常需要量化,其次,实际的决策树可能会更复杂,比如判断条件可能有多个分支等。
通过上面的例子,我们大概可以知道,决策树是一种树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。
2、决策树构造
决策树的构造过程不依赖领域知识,它使用属性选择度量来选择将元组最好地划分成不同的类的属性。所谓决策树的构造就是进行属性选择度量确定各个特征属性之间的拓扑结构。
构造决策树的关键步骤是分裂属性。所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支,其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。分裂属性分为三种不同的情况:
- 属性是离散值且不要求生成二叉决策树。此时用属性的每一个划分作为一个分支。
- 属性是离散值且要求生成二叉决策树。此时使用属性划分的一个子集进行测试,按照“属于此子集”和“不属于此子集”分成两个分支。
- 属性是连续值。此时确定一个值作为分裂点split point,按照>split point和<=split point生成两个分支。
构造决策树的关键性内容是进行属性选择度量,属性选择度量是一种选择分裂准则,是将给定了类标记的训练集合划分,“最好”地分成个体类的启发式方法,它决定了拓扑结构及分裂点split point的选择。
属性选择度量算法有很多,一般使用自顶向下递归分治法,并采用不回溯的贪心策略,常用的算法有ID3和C4.5,有关这个两个算法的介绍大家可以去看看这篇文章,讲得还不错:
【机器学习】决策树(上)——ID3、C4.5、CART(非常详细)
在实际构造决策树时,通常要进行剪枝,这是为了处理由于数据中的噪声和离群点导致的过分拟合问题。剪枝有两种:
- 预剪枝——在构造过程中,当某个节点满足剪枝条件,则直接停止此分支的构造。预剪枝不仅可以降低过拟合的风险而且还可以减少训练时间,但另一方面它是基于“贪心”策略,会带来欠拟合风险。
- 后剪枝——先构造完成完整的决策树,再通过某些条件遍历树进行剪枝。后剪枝决策树的欠拟合风险很小,泛化性能往往优于预剪枝决策树。但同时其训练时间会大的多。
3、交叉验证
因为在实际的训练中,训练的结果对于训练集的拟合程度通常还是挺好的(初试条件敏感),但是对于训练集之外的数据的拟合程度通常就不那么令人满意了。因此我们通常并不会把所有的数据集都拿来训练,而是分出一部分来(这一部分不参加训练)对训练集生成的参数进行测试,相对客观的判断这些参数对训练集之外的数据的符合程度。这种思想就称为交叉验证。
交叉验证一般在数据不充足的时候使用,可以选择交叉验证来训练忧患选择模型,如果数据很充足则会选择将数据随机分成三份即训练集、验证集和测试集。
交叉验证有以下三种方法:
- 简单交叉验证:也是最常用的交叉验证方法,我们在之前的深度学习中就曾使用过,那就是随机将样本数据分成两个部分,7:3的比例训练集和测试集,然后用训练集来训练模型,在测试集上验证模型及参数。接着,我们再把样本打乱,重新选择训练集和测试集,继续训练数据和检验模型。最后我们选择损失函数评估最优的模型和参数。
- S折交叉验证:和第一种方法不同,S折交叉验证会把样本数据随机的分成S份,每次随机的选择S-1份作为训练集,剩下的1份做测试集。当这一轮完成后,重新随机选择S-1份来训练数据。若干轮(小于S)之后,选择损失函数评估最优的模型和参数。
- 留一交叉验证:它是第二种情况的特例,此时S等于样本数N,这样对于N个样本,每次选择N-1个样本来训练数据,留一个样本来验证模型预测的好坏。此方法主要用于样本量非常少的情况,比如对于普通适中的问题,N小于50时,我一般采用留一交叉验证。
通过反复的交叉验证,用损失函数来度量得到的模型的好坏,最终我们可以得到一个较好的模型。那这三种情况,到底我们应该选择哪一种方法呢?一句话总结,如果我们只是对数据做一个初步的模型建立,不是要做深入分析的话,简单交叉验证就可以了。否则就用S折交叉验证。在样本量少的时候,使用S折交叉验证的特例留一交叉验证。
三、决策树算法函数介绍
这里主要介绍其中两个函数。
1、 train_test_split函数
train_test_split来自sklearn.model_selection,是交叉验证中常用的函数,它能从样本中按比例随机选取训练集和测试集,它的用法如下:
X_train, X_test, y_train, y_test = cross_validation.train_test_split(train_data, train_target, test_size=0.25, random_state=None
其函数内参数介绍:
| 参数名 | 说明 |
|---|---|
| train_data | 所要划分的样本特征集 |
| train_target | 所要划分的样本结果 |
| test_size | 样本占比,如果是整数的话就是样本的数量 |
| random_state | 是随机数的种子 |
我们用代码来举个例子:
import numpy as np
from sklearn.model_selection import train_test_split
x, y = np.arange(10).reshape(5, 2), range(5)
print("原始数据为:\n x -> {} \n y -> {}".format(x, list(y)))
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.33, random_state=42)
print("得到的训练数据为:\n x_train -> {} \n y_train -> {}".format(x_train, y_train))
print("得到的测试数据为:\n x_text -> {} \n y_test -> {}".format(x_test, y_test))
它运行的结果是:
原始数据为:
x -> [[0 1]
[2 3]
[4 5]
[6 7]
[8 9]]
y -> [0, 1, 2, 3, 4]
得到的训练数据为:
x_train -> [[4 5]
[0 1]
[6 7]]
y_train -> [2, 0, 3]
得到的测试数据为:
x_text -> [[2 3]
[8 9]]
y_test -> [1, 4]
2、tree.DecisionTreeClassifier函数
DecisionTreeClassifier函数用于创建决策树分类器,默认使用CART算法。它的用法如下:
sklearn.tree.DecisionTreeClassifier(criterion=’gini’,splitter=’best’,max_depth=None,min_samples_split=2,min_samples_leaf=1,min_weight_fraction_leaf=0.0,max_features=None,random_state=None,max_leaf_nodes=None,min_impurity_decrease=0.0,min_impurity_split=None,class_weight=None,presort=False)
这个函数的参数很多,我们目前只介绍一下其中几个常用的参数:
| 参数名 | 说明 |
|---|---|
| criterion | string类型,可选(默认为"gini")。指定使用哪种方法衡量分类的质量。支持的标准有"gini"代表的是Gini impurity(不纯度)与"entropy"代表的是information gain(信息增益) |
| splitter | string类型,可选(默认为"best")。指定在节点中选择分类的策略。支持的策略有"best",选择最好的分类,"random"选择最好的随机分类 |
| max_depth | int or None,可选(默认为"None")。表示树的最大深度 |
| min_samples_split | int,float,可选(默认为2)。一个内部节点需要的最少的样本数 |
| max_features | int,float,string or None类型,可选(默认为None)。在进行分类时需要考虑的特征数 |
| random_state | 可为int类型,RandomState 实例或None,可选(默认为"None")。如果是int,random_state是随机数字发生器的种子;如果是RandomState,random_state是随机数字发生器,如果是None,随机数字发生器是np.random使用的RandomState instance |
我们也举个例子看看:
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier(random_state=0)
iris = load_iris()
cross_val_score(clf, iris.data, iris.target, cv=10)
print("Cross-val score for iris: ", cross_val_score(clf, iris.data, iris.target, cv=10))
它运行的结果是:
Cross-val score for iris: [1. 0.93333333 1. 0.93333333 0.93333333 0.86666667
0.93333333 1. 1. 1. ]
四、数据说明
我们在使用决策树函数时,其中会用到一个数据集——iris,它是一个经典的用于多分类的数据集,通过sklearn.datasets.load_iris()函数可导入。sklearn中的iris数据集有5个key,分别如下:
| key | 说明 |
|---|---|
| target_names | 类别名称,分别为setosa、versicolor和virginica |
| data | 特征集,5列,150行 |
| target | 样本类别值 |
| DESCR | 关于数据的描述信息 |
| feature_names | 特征名称,分别为sepal length (cm),sepal width (cm),petal length (cm)和petal width (cm) |
iris.data前五条数据如下:
from sklearn.datasets import load_iris
dataset = load_iris()
print(dataset.data[0: 5])
它运行的结果是:
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
iris.target前五条数据如下:
from sklearn.datasets import load_iris
dataset = load_iris()
print(dataset.target[0: 5])
它运行的结果是:
[0 0 0 0 0]
五、编写Python决策树程序并运行
我们仍然使用软件MobaXterm连接master服务器,然后使用如下命令开始编写我们的程序:
vi decisionTree.py
然后输入如下Python代码:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from sklearn import tree
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import numpy as np
if __name__=="__main__":
# 加载数据
dataset = load_iris()
# 提取属性数据
X = dataset.data
# 提取标签数据
y = dataset.target
# train_test_split函数用于划分数据集为训练集和测试集,其中参数test_size默认为0.25,表示将25%的数据划分为测试集
Xd_train, Xd_test, y_train, y_test = train_test_split(X, y, random_state=14)
# 创建决策树分类器
clf = tree.DecisionTreeClassifier()
# 训练分类器模型
clf = clf.fit(Xd_train, y_train)
y_predicted = clf.predict(Xd_test)
# 计算预测准确率
accuracy = np.mean(y_predicted == y_test) * 100
print("y_test ",y_test)
print("y_predicted",y_predicted)
print("accuracy:",accuracy)
输入完之后保存退出。
然后在终端使用如下命令进行运行该程序:
python decisionTree.py
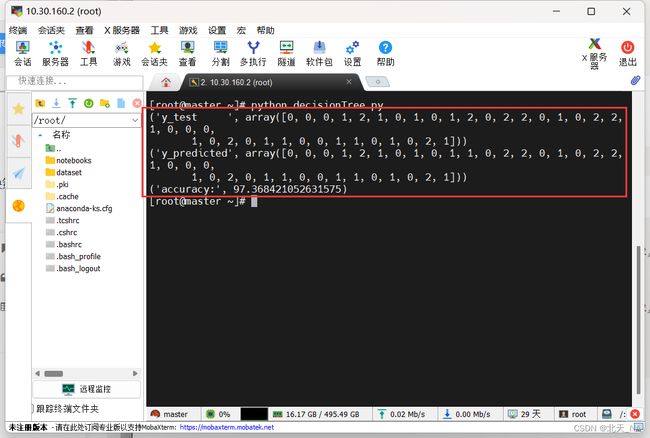
它运行的结果是:
[root@master ~]# python decisionTree.py
('y_test ', array([0, 0, 0, 1, 2, 1, 0, 1, 0, 1, 2, 0, 2, 2, 0, 1, 0, 2, 2, 1, 0, 0, 0,
1, 0, 2, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 2, 1]))
('y_predicted', array([0, 0, 0, 1, 2, 1, 0, 1, 0, 1, 1, 0, 2, 2, 0, 1, 0, 2, 2, 1, 0, 0, 0,
1, 0, 2, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 2, 1]))
('accuracy:', 97.368421052631575)
六、最后我想说
有关决策树的优缺点大家可以去看一下这篇文章:关于决策树的优缺点
机器学习中,决策树是一个预测模型;他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象,而每个分叉路径则代表的某个可能的属性值,而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出,若欲有复数输出,可以建立独立的决策树以处理不同输出。数据挖掘中决策树是一种经常要用到的技术,可以用于分析数据,同样也可以用来作预测。
决策树是一种简单高效并且具有强解释性的模型,广泛应用于数据分析领域。 其本质是一颗由多个判断节点组成的树,可以是二叉树或非二叉树。 其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。
更多的知识大家自行上网学习,我就介绍这么多了,后续还会更新其他的Python算法的,期待得到大家的支持,谢谢!