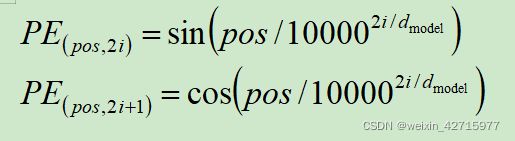Transformer中的position encoding(位置编码一)
本文主要讲解Transformer 中的 position encoding,在当今CV的目标检测最前沿,都离不开position encoding,在DETR,VIT,MAE框架中应用广泛,下面谈谈我的理解。
一般position encoding 分为 正余弦编码和可学习编码。
正余弦编码
以下为DETR中的position encoding过程,本文将以简单的数据帮助大家理解。以下过程是按照DETR走的,为了更好理解,对数据进行简化,针对不同的图像,产生不同的数据大小。
1.创建mask
假设mask为4×4大小,输入图像大小为3×3。
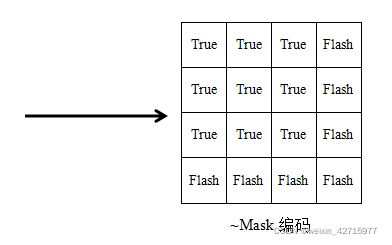
下图为mask生成的4*4维度的矩阵,根据对应与输入图像大小3*3生成以下的mask编码tensor,下右图为反mask编码tensor,这一步就得到了图像的大小及对应与mask下的位置。
2.生成Y_embed和X_embed的tensor
y_embed = not_mask.cumsum(1, dtype=torch.float32)#在行方向累加#(b , h , w)
x_embed = not_mask.cumsum(2, dtype=torch.float32)#在列方向累加#(b , h , w)DETR中运用两行编码实现Y_embed和X_embed,生成大小为(bitch_size , h , w)的tensor。
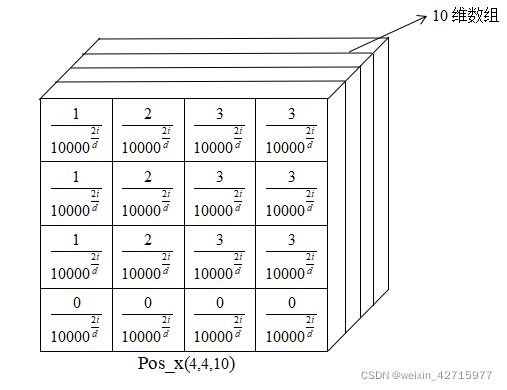
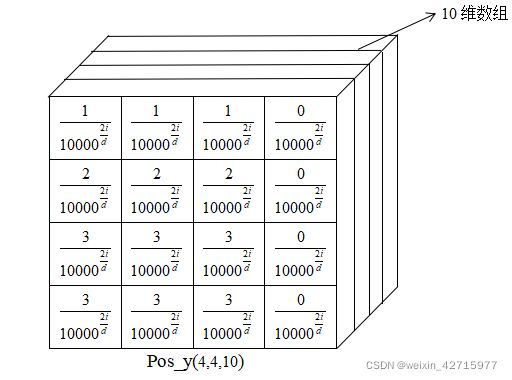
根据在1中我们产生的反mask编码,生成的Y_embed和X_embed如下。
Y_embed对为mask编码True的进行行方向累加1,X_embed对为mask编码True的进行列方向累加1。下图所示:
3. 运用10维(自己可以延申为1024维)position进行编码
num_pos_feats = 10
temperature = 10000
dim_t = torch.arange(num_pos_feats, dtype=torch.float32,device=a.device)#生成10维数
dim_t = temperature ** (2 * (dim_t // 2) / num_pos_feats) #i=dim_t // 2#对10维数进行计算 第三行代码生成了10个tensor数据,第四行代码相当于![]() ,对10个生成的tensor进行计算得到位置编码公式中的分母
,对10个生成的tensor进行计算得到位置编码公式中的分母![]() ,结果如下。
,结果如下。![]()
4.生成pos_x以及pos_y
pos_x = x_embed[:, :, None] / dim_t
pos_y = y_embed[:, :, None] / dim_t
pos_x = torch.stack((pos_x[:, :, 0::2].sin(), pos_x[:, :, 1::2].cos()), dim=3).flatten(2)#不降维
pos_y = torch.stack((pos_y[:, :, 0::2].sin(), pos_y[:, :, 1::2].cos()), dim=3).flatten(2)#不降维第四步以后的直观效果如上图所示,可以对照第二步的X_embed和Y_embed,会发现pos_x,y的tensor分母和X,Y_embed对应 ,很好理解,其中i对应的是10维position的不同维度的数,d代表的是position编码维度。
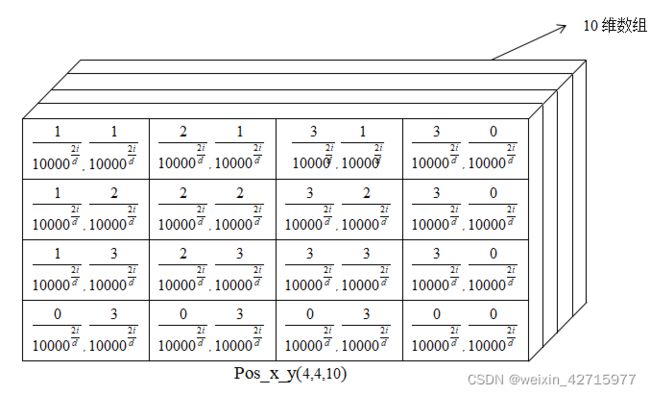
5.组合Pos_x和Pos_y
因为上述位置编码的生成是行列方向分开的,这一步需要进行组合。
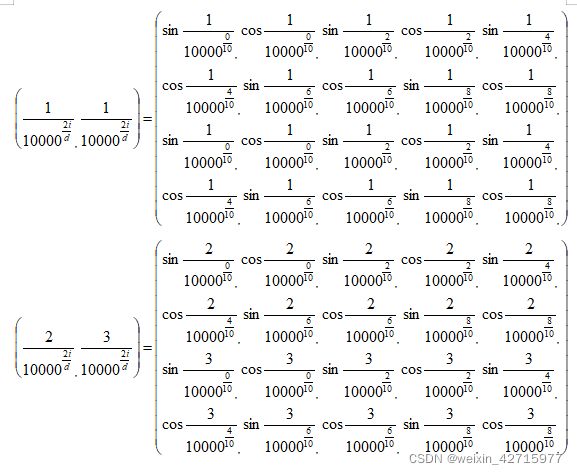
pos = torch.cat((pos_y, pos_x), dim=2)组合以后直观图的样子如上,这时会发现16个位置的分母已经根据pos的不同,达到了位置编码的不同,因为本文采用的是10维的position,分子i的范围为0-10,每个位置就形成了1*20的tensor数据。
上述两个位置的编码就可以理解为1*20的tensor数据,因为比较长,分开写了,不是4*5的,而是1*20的tensor数据,通过上图可以很直观的理解position encoding。
程序结果如下,类似于此。下面将自己改写的简单的position encoding 程序段放在下面,大家可以复制自己跑一下,看看输出结果,加强理解。
import torch
import numpy as np
import math
#正余弦位置编码
num_pos_feats = 10
temperature = 10000
normalize = False
scale = 2 * math.pi
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
a = torch.tensor(a)
mask = [[False,False,False,True],[False,False,False,True],[False,False,False,True],[True,True,True,True]]
mask = torch.tensor(mask)
print(mask)
assert mask is not None
not_mask = ~mask
print(not_mask)
y_embed = not_mask.cumsum(0, dtype=torch.float32)
x_embed = not_mask.cumsum(1, dtype=torch.float32)
print(y_embed)
print(x_embed)
if normalize:
eps = 1e-6
# b = a[i:j:s]表示:i,j与上面的一样,但s表示步进,缺省为1.
# 所以a[i:j:1]相当于a[i:j]
# 当s<0时,i缺省时,默认为-1. j缺省时,默认为-len(a)-1
# 所以a[::-1]相当于 a[-1:-len(a)-1:-1],也就是从最后一个元素到第一个元素复制一遍,即倒序。
# 对于X[:,:,m:n]是取三维矩阵中第m维到第n-1维的所有数据
# 归一化
y_embed = y_embed / (y_embed[-1:, :] + eps) * scale # y_embed[:, -1:, :]代表取三维数据中的最后一行数据
x_embed = x_embed / (x_embed[:, -1:] + eps) * scale # x_embed[:, :, -1:]代表取三维数据中的最后一列数据
print(y_embed)
print(x_embed)
dim_t1 = torch.arange(num_pos_feats, dtype=torch.float32,device=a.device)
print(dim_t1)
dim_t = temperature ** (2 * (dim_t1 // 2) / num_pos_feats) #i=dim_t1 // 2
print(dim_t)
pos_x = x_embed[:, :, None] / dim_t
pos_y = y_embed[:, :, None] / dim_t
print(pos_x)
print(pos_y)
pos_x = torch.stack((pos_x[:, :, 0::2].sin(), pos_x[:, :, 1::2].cos()), dim=3).flatten(2)#不降维
pos_y = torch.stack((pos_y[:, :, 0::2].sin(), pos_y[:, :, 1::2].cos()), dim=3).flatten(2)#不降维
print(pos_x)
print(pos_y)
pos = torch.cat((pos_y, pos_x), dim=2)
print(pos)
以上是我的理解,欢迎大家批评指正,互相交流!Transformer中的position encoding(位置编码二)_zuoyou-HPU的博客-CSDN博客本文依旧采用4*4大小的词嵌入模型,和模仿3*3大小的特征图进行解读——可学习编码1.根据自己模型中的定义的最大特征图大小进而定义词嵌入模型大小。假设模型中的特征图大小不超过4*4,那么我定义的词嵌入模型大小就为4*4,同正余弦编码一样,采用10维数据进行编码。生成行方向的词嵌入模型(4 ,10),及生成列方向的词嵌入模型(4 , 10),进而生成4*10的随机权重值并均匀分布在0-1之间。row_embed = nn.Embedding(4, 10)#生成行方向词嵌入模型col_embe.https://blog.csdn.net/weixin_42715977/article/details/122139883?spm=1001.2014.3001.5501
Swin Transformer 中的 shift window attention_zuoyou-HPU的博客-CSDN博客https://blog.csdn.net/weixin_42715977/article/details/124151870?spm=1001.2014.3001.5502