PINN(Python通过递归神经网络直接实现常微分方程积分)

 Python构建PINN：（1）加载工具包；（2）搭建基于物理定律的模型结构；（3）将数据驱动内核与基于物理的内核耦合（PINN）；（4）搭建神经网络；（5）使用训练好的神经网络预测

 

（1）、加载工具包

import pandas as pd  #用于数据导入和操作的pandas

import numpy as np  #用于数据导入和操作的numpy

import matplotlib.pyplot as plt

#专门化模型

from tensorflow.keras.layers import RNN, Dense, Layer

from tensorflow.keras import Sequential  #使用models.Sequential()来搭建神经网络

from tensorflow.keras.optimizers import RMSprop  #超参数优化

from tensorflow.python.framework import tensor_shape

from tensorflow import float32, concat, convert_to_tensor  #数据类型（浮点型32位）、拼接两个矩阵、  将python的数据类型（列表和矩阵）转换成  TensorFlow可用的tensor数据类型

 

（2）、搭建数据驱动的欧拉公式结构

#欧拉积分单元

class EulerIntegratorCell(Layer):

    def __init__(self, C, m, dKlayer, a0=None, units=1, **kwargs):

def call(self, inputs, states):  #构造公式

        inputs  = convert_to_tensor(inputs)  #将python的数据类型（列表和矩阵）转换成TensorFlow可用的  tensor数据类型

        a_tm1   = convert_to_tensor(states)

        x_d_tm1 = concat((inputs, a_tm1[0, :]), axis=1)  #按列拼接两个矩阵：aixs=d 这项参数，表示沿着第d+1(d=-  1表示倒数第一维)维的方向操作。       

        dk_t    = self.dKlayer(x_d_tm1)

        da_t    = self.C * (dk_t ** self.m)

        a       = da_t + a_tm1[0, :]

        return a, [a]

    def get_initial_state(self, inputs=None, batch_size=None, dtype=None)  #令初始状态为零#batch_size：样  本数量，即维度

        return self.a0

 

（3）、使用来自EulerIntegratorCell的对象，并将其与RNN耦合，创建一个可供训练的模型

#使用model.compile()方法来配置训练方法

def create_model(C, m, a0, dKlayer, batch_input_shape, return_sequences=False, return_state=False):

    euler = EulerIntegratorCell(C=C, m=m, dKlayer=dKlayer, a0=a0, batch_input_shape=batch_input_shape)

  #batch_input_shape来增强输入的形状

    PINN  = RNN(cell=euler, batch_input_shape=batch_input_shape, return_sequences=return_sequences,   return_state=return_state)

    model = Sequential()

    model.add(PINN)

    model.compile(loss='mse', optimizer=RMSprop(1e-2))  #使用model.compile()方法来配置训练方法：使用  RMSprop优化器(起到的效果是在参数空间更为平缓  的方向，会取得更大的进步)，学习率为1e-2

    return model

 

（4）、使用models.Sequential()来搭建神经网络

    dKlayer = Sequential()  #初始化dKlayer，准备按顺序接收不同的层

    dKlayer.add(Normalization(np.min(Strain), np.max(Strain), np.min(atrain), np.max(atrain)))

    dKlayer.add(Dense(5, activation='tanh’))  #model.add，添加层，增加了第一层5个神经元  （tanh作为激活函数）输出，全连接层  Dense定义  神经网络的一层

    dKlayer.add(Dense(1))  #添加第二层1个神经元输入

 

5）、使用训练好的模型预测

# fitting physics-informed neural network #使用model.fit()方法来执行训练过程

    model = create_model(C=C, m=m, a0=convert_to_tensor(a0, dtype=float32), dKlayer=dKlayer,   batch_input_shape=Strain.shape)  #创建混合物理信息神经网络模型

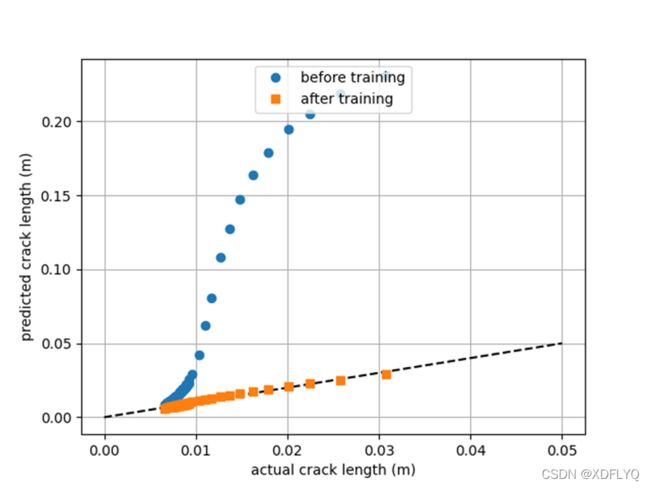
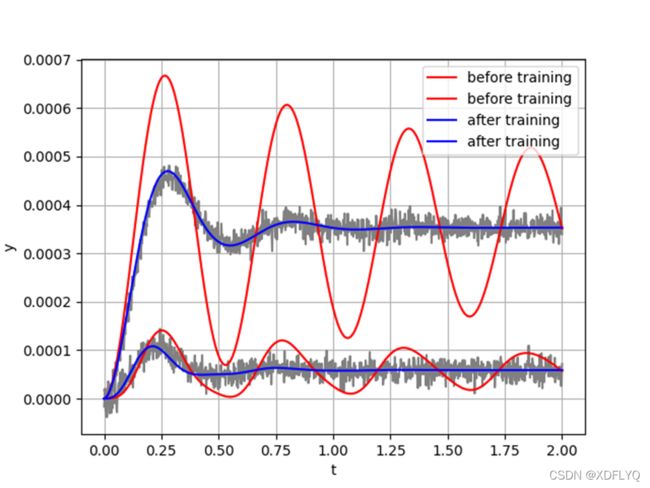
    aPred_before = model.predict_on_batch(Strain)[:,:]  #训练前后检查训练集的预测

    model.fit(Strain, atrain, epochs=100, steps_per_epoch=1, verbose=1)  #模型已经准备好接受培训，使  用model.fit()方法来执行训练过程   

    aPred = model.predict_on_batch(Strain)[:,:]  #训练前后检查训练集的预测

 

 

 

 

 

 

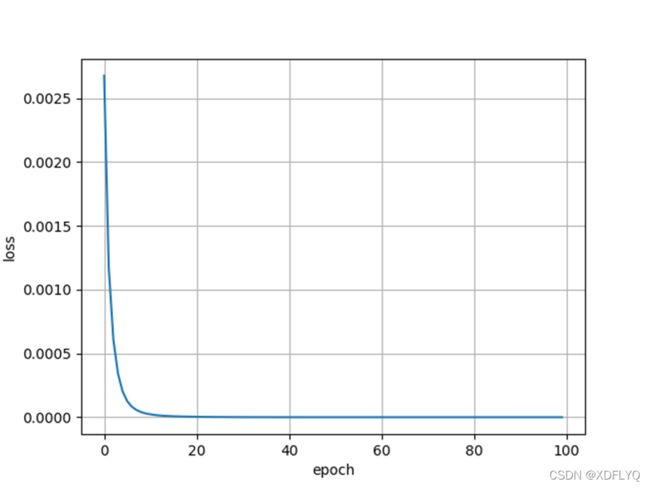
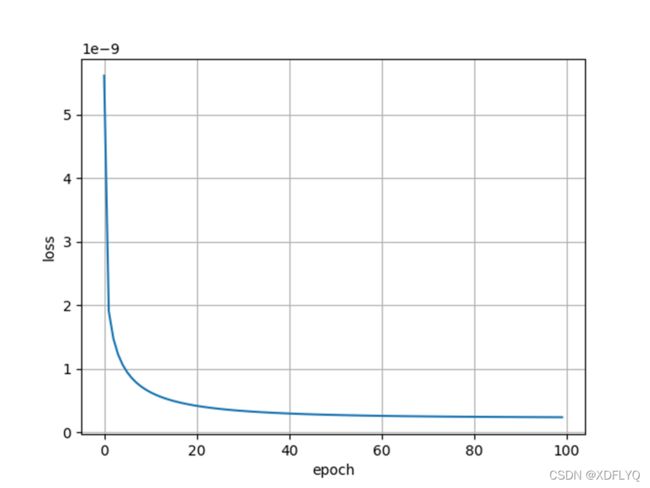
 损失在20个时期内迅速收敛，40个时期后仅略有改善

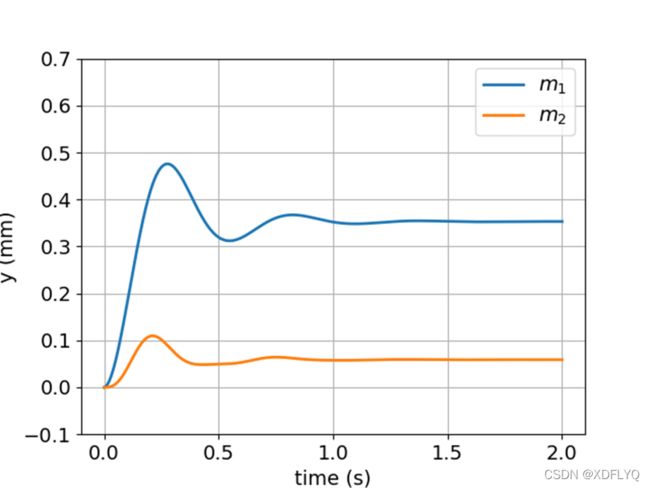
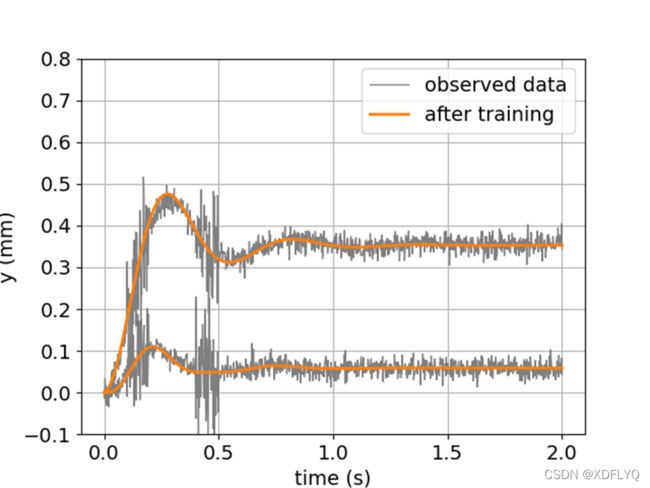
 对实际位移的预测

 

 

 数据损坏发生在两个不同的时间段（0.1s到0.2s)和(0.4s到0.5s）