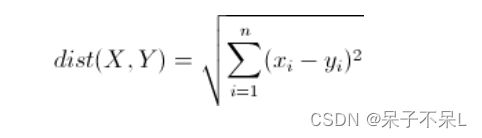机器学习 —— K-近邻算法（KNN）

编辑器：jupyter notebook 

• 导入数据分析三剑客

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

0、导引

如何进行电影分类

众所周知，电影可以按照题材分类，然而题材本身是如何定义的?由谁来判定某部电影属于哪个题材? 也就是说同一题材的电影具有哪些公共特征?这些都是在进行电影分类时必须要考虑的问题。 没有哪个电影人会说自己制作的电影和以前的某部电影类似，但我们确实知道每部电影在风格上的确有可能会和同题材的电影相近。 那么动作片具有哪些共有特征，使得动作片之间非常类似，而与爱情片存在着明显的差别呢？动作片中也会存在接吻镜头，爱情片中也会存在打斗场景，我们 不能单纯依靠是否存在打斗或者亲吻来判断影片的类型。但是爱情片中的亲吻镜头更多，动作片中 的打斗场景也更频繁，基于此类场景在某部电影中出现的次数可以用来进行电影分类。

本章介绍第一个机器学习算法：K-近邻算法，它非常有效而且易于掌握。

KNN算法

# sklearn：机器学习库
from sklearn.neighbors import KNeighborsClassifier

# 导入电影数据
movie = pd.read_excel('../data/movies.xlsx',sheet_name=1)
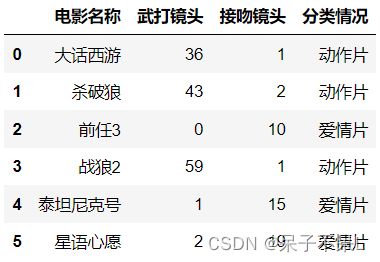
movie

# 有监督学习：data, target(label)标签

# data
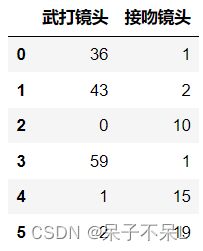
data = movie[['武打镜头','接吻镜头']]
data

# target
# target = movie.分类情况
target = movie['分类情况']
target
'''
0    动作片
1    动作片
2    爱情片
3    动作片
4    爱情片
5    爱情片
Name: 分类情况, dtype: object
'''

data.shape, target.shape
# ((6, 2), (6,))

# 使用 KNN 算法
# 1.创建 KNN 对象
# n_neighbors=5 : K的值，k = 5
# p=2 : 默认使用欧氏距离，p=1表示曼哈顿距离
knn = KNeighborsClassifier(n_neighbors=5,p=2)   # 分类多则将k适当增大

# 2.训练数据（历史数据）
# 注意：(1)data和target行数必须一致 (2)data必须是二维
knn.fit(X=data,y=target)

# 3.预测新数据
# 提供预测数据
X_test = np.array([[50,1],[1,20],[30,1],[2,10],[20,10]])
y_test = np.array(['动作片', '爱情片', '动作片', '爱情片', '动作片'])
# 预测：predict
y_pred = knn.predict(X_test)
y_pred
# array(['动作片', '爱情片', '动作片', '爱情片', '爱情片'], dtype=object)

# 预测数据
# X_test：测试集中的数据
# y_test：测试集中数据对应的真是结果
# y_pred：测试集中数据对应的预测结果

# 训练数据
# data，target：一般是全部数据
# x_train：训练集中的数据
# y_train：训练集中数据对应的结果

# 4.计算得分：score
knn.score(X_test,y_test)
# 准确率：0.8 = 80%

1、k-近邻算法原理

简单地说，K-近邻算法采用测量不同特征值之间的距离方法进行分类。

• 优点：精度高、对异常值不敏感。
• 缺点：时间复杂度高、空间复杂度高。
• 适用数据范围：数值型和标称型。

工作原理

存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据 与所属分类的对应关系。输人没有标签的新数据后，将新数据的每个特征与样本集中数据对应的 特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签。一般来说，我们 只选择样本数据集中前K个最相似的数据，这就是K-近邻算法中K的出处,通常K是不大于20的整数。 最后 ，选择K个最相似数据中出现次数最多的分类，作为新数据的分类。

回到前面电影分类的例子，使用K-近邻算法分类爱情片和动作片。有人曾经统计过很多电影的打斗镜头和接吻镜头，下图显示了6部电影的打斗和接吻次数。假如有一部未看过的电影，如何确定它是爱情片还是动作片呢？我们可以使用K-近邻算法来解决这个问题。

 首先我们需要知道这个未知电影存在多少个打斗镜头和接吻镜头，上图中问号位置是该未知电影出现的镜头数图形化展示，具体数字参见下表。

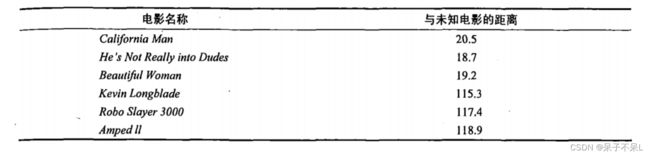
 即使不知道未知电影属于哪种类型，我们也可以通过某种方法计算出来。首先计算未知电影与样本集中其他电影的距离，如图所示。

现在我们得到了样本集中所有电影与未知电影的距离，按照距离递增排序，可以找到K个距 离最近的电影。假定k=3，则三个最靠近的电影依次是California Man、He's Not Really into Dudes、Beautiful Woman。K-近邻算法按照距离最近的三部电影的类型，决定未知电影的类型，而这三部电影全是爱情片，因此我们判定未知电影是爱情片。

欧几里得距离(Euclidean Distance)

欧氏距离是最常见的距离度量，衡量的是多维空间中各个点之间的绝对距离。公式如下：

 

2、在scikit-learn库中使用k-近邻算法

• 分类问题：from sklearn.neighbors import KNeighborsClassifier

• 回归问题：from sklearn.neighbors import KNeighborsRegressor

1）用于分类

• 导包，机器学习的算法KNN、数据 鸢(yuan)尾花
  • from sklearn.datasets import load_iris
• 定义KNN分类器
• 拆分数据集
  • 将数据集进行拆分成训练数据和测试数据
  • from sklearn.model_selection import train_test_split
• 绘制图形

# datasets: 数据集
from sklearn.datasets import load_iris


# 导入数据
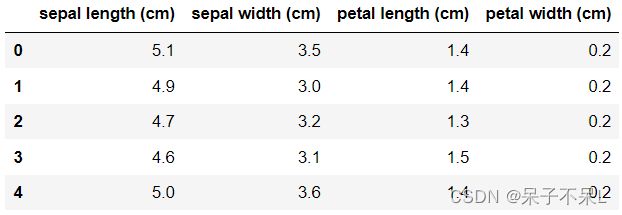
iris = load_iris()


data = iris['data']
target = iris['target']
target_names = iris['target_names']
feature_names = iris['feature_names']


data.shape, target.shape
# ((150, 4), (150,))


data
target

# 0,1,2 三种分类
target_names    # array(['setosa', 'versicolor', 'virginica'], dtype='

 

拆分数据集

from sklearn.model_selection import train_test_split


# test_size:   int:测试数据的条数 ；float：测试数据所占的比例

# 训练数据：x_train,y_train
# 测试数据：x_test,y_test
x_train,x_test,y_train,y_test = train_test_split(data,target,test_size=0.2)  # 按条件随机分配数据
x_train.shape,x_test.shape  # ((120, 4), (30, 4))


# KNN
knn = KNeighborsClassifier()
knn.fit(x_train,y_train)


# 预测
y_pred = knn.predict(x_test)
y_pred
'''
array([1, 0, 2, 0, 2, 1, 1, 1, 1, 0, 2, 0, 0, 2, 2, 2, 2, 2, 2, 0, 0, 0,
       2, 2, 0, 2, 0, 0, 1, 2])
'''


# 得分
knn.score(x_test,y_test)   # 0.9666666666666667

2）KNN用于回归

• 回归：用于对趋势的预测

from sklearn.neighbors import KNeighborsRegressor


# sin曲线
x_train = np.random.random(100)*10
y_train = np.sin(x_train)

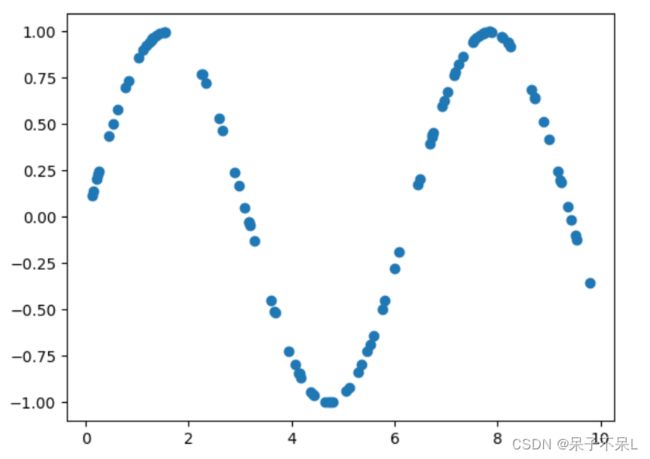
# 画图
plt.scatter(x_train,y_train)

 

 

x_train.shape, y_train.shape # ((100,), (100,))
# x_train 一维
# y_train 一维


# x_train ——> n行1列
# x_train = x_train.reshape(100,1)
x_train = x_train.reshape(-1,1)

# KNN 回归
knn = KNeighborsRegressor()
# 训练
knn.fit(x_train,y_train)     # data 参数必须是二维


# 预测
x_test = np.linspace(0,10,100)

y_pred = knn.predict(x_test.reshape(-1,1))
y_pred
'''
array([ 0.18785425,  0.18785425,  0.18785425,  0.25239521,  0.32461517,
        0.49322517,  0.59020695,  0.59020695,  0.67372961,  0.82216096,
        0.87152551,  0.91665299,  0.93701395,  0.96175666,  0.98735223,
        0.99413828,  0.99413828,  0.99413828,  0.95257683,  0.90811219,
        0.85357553,  0.65346137,  0.65346137,  0.65346137,  0.65346137,
        0.65346137,  0.42664993,  0.29191087,  0.29191087,  0.08136332,
        0.08136332, -0.03546732, -0.03546732, -0.03546732, -0.32873543,
       -0.32873543, -0.46400637, -0.59715   , -0.59715   , -0.8135771 ,
       -0.8135771 , -0.8135771 , -0.89059278, -0.9143527 , -0.94475893,
       -0.9719159 , -0.99058708, -0.99058708, -0.98616717, -0.97034101,
       -0.93705209, -0.84248747, -0.84248747, -0.73685134, -0.73685134,
       -0.6701099 , -0.60096691, -0.51179692, -0.41183888, -0.41183888,
       -0.24825372, -0.10716138,  0.06254564,  0.06254564,  0.33043731,
        0.33043731,  0.38635598,  0.46476227,  0.51147407,  0.68981736,
        0.68981736,  0.78227693,  0.83601007,  0.87446203,  0.9425628 ,
        0.96790843,  0.98562532,  0.99220318,  0.99567278,  0.97623229,
        0.94841973,  0.94841973,  0.94841973,  0.89139115,  0.76660054,
        0.68123704,  0.5808656 ,  0.5808656 ,  0.5808656 ,  0.31270245,
        0.31270245,  0.22097909,  0.1347291 ,  0.00238115,  0.00238115,
       -0.10584598, -0.10584598, -0.10584598, -0.10584598, -0.10584598])
'''


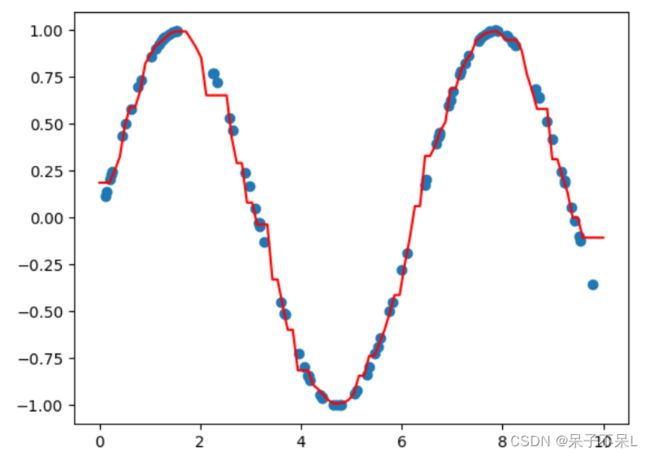
# 画图
plt.scatter(x_train,y_train)

plt.plot(x_test,y_pred,c='r')

• 图片处理

# 图片

# 读取图片数据
img = plt.imread('../iris.png')
img.shape # (658, 1270, 4)

# 0 — 255 RGB 红绿蓝 int
# 0 — 1 float


# 显示图片
plt.imshow(img)

# 将前两个维度整合
img2 = img.reshape(-1,4)
img2.shape
# (835660, 4)

练习： 预测年收入是否大于50K美元

1.读取adults.txt文件，最后一列是年收入，并使用KNN算法训练模型，然后使用模型预测一个人的年收入是否大于50

df = pd.read_csv('../data/adults.txt')
df.shape
# (32561, 15)

df.sample(5)    # 随即查看五条

df.dtypes
'''
age                int64
workclass         object
final_weight       int64
education         object
education_num      int64
marital_status    object
occupation        object
relationship      object
race              object
sex               object
capital_gain       int64
capital_loss       int64
hours_per_week     int64
native_country    object
salary            object
dtype: object
'''

df.info()
'''

RangeIndex: 32561 entries, 0 to 32560
Data columns (total 15 columns):
 #   Column          Non-Null Count  Dtype 
---  ------          --------------  ----- 
 0   age             32561 non-null  int64 
 1   workclass       32561 non-null  object
 2   final_weight    32561 non-null  int64 
 3   education       32561 non-null  object
 4   education_num   32561 non-null  int64 
 5   marital_status  32561 non-null  object
 6   occupation      32561 non-null  object
 7   relationship    32561 non-null  object
 8   race            32561 non-null  object
 9   sex             32561 non-null  object
 10  capital_gain    32561 non-null  int64 
 11  capital_loss    32561 non-null  int64 
 12  hours_per_week  32561 non-null  int64 
 13  native_country  32561 non-null  object
 14  salary          32561 non-null  object
dtypes: int64(6), object(9)
memory usage: 3.7+ MB
'''

df.isnull().sum()
'''
age               0
workclass         0
final_weight      0
education         0
education_num     0
marital_status    0
occupation        0
relationship      0
race              0
sex               0
capital_gain      0
capital_loss      0
hours_per_week    0
native_country    0
salary            0
dtype: int64
'''

2.获取年龄age、教育程度education、职位workclass、每周工作时间hours_per_week 作为机器学习数据 获取薪水作为对应结果

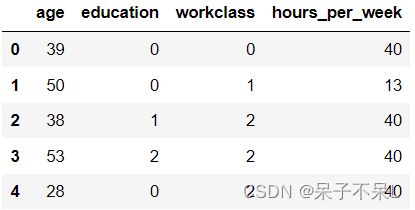
data = df[['age','education','workclass','hours_per_week']].copy()
target = df['salary'].copy()

data.head()

 

3.数据转换，将String/Object类型数据转换为int,用0,1,2,3...表示

• 使用factorize()函数

data.education.unique()
'''
array(['Bachelors', 'HS-grad', '11th', 'Masters', '9th', 'Some-college',
       'Assoc-acdm', 'Assoc-voc', '7th-8th', 'Doctorate', 'Prof-school',
       '5th-6th', '10th', '1st-4th', 'Preschool', '12th'], dtype=object)
'''

# education
data.education = data.education.factorize()[0]

# workclass
data.workclass = data.workclass.factorize()[0]

data.head()

4.拆分数据集：训练数据和预测数据

• train_test_split

x_train, x_test, y_train, y_test = train_test_split(data,target,test_size=0.2)
x_train.shape, x_test.shape
# ((26048, 4), (6513, 4))

5.使用KNN算法

knn = KNeighborsClassifier()
knn.fit(x_train,y_train)

knn.predict(x_test)
# array(['<=50K', '>50K', '<=50K', ..., '>50K', '>50K', '<=50K'], dtype=object)

# 得分
# 测试集得分
knn.score(x_test,y_test)
# 0.7618608935974206

# 训练集得分
knn.score(x_train,y_train)
# 0.8178363022113022

6.保存训练模型

• import joblib
• 保存模型： joblib.dump(knn, 'knn.plk')
• 导入模型： joblib.load('knn.plk')

import joblib

# 保存模型
joblib.dump(knn,'knn.plk')
# ['knn.plk']

# 导入模型
knn2 = joblib.load('knn.plk')

knn2.predict(x_test)
'''
array(['<=50K', '>50K', '<=50K', ..., '>50K', '>50K', '<=50K'],
      dtype=object)
'''