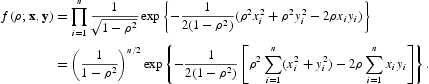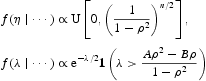拓端tecdat|R语言Copula的贝叶斯非参数估计

 全文链接：http://tecdat.cn/?p=4190

Copula可以完全表征多个变量的依赖性。本文的目的是提供一种贝叶斯非参数方法来估计一个copula，我们通过混合一类参数copula来做到这一点。特别地，我们表明任何双变量copula密度可以通过高斯copula密度函数的无限混合任意精确地近似。该模型可以通过马尔可夫链蒙特卡罗方法估计，并且该模型在模拟和实际数据集上进行演示。

相关视频：Copula算法原理和R语言股市收益率相依性可视化分析

Copula算法原理和R语言股市收益率相依性可视化分析

，时长16:34

关键词：贝叶斯非参数估计， Copula ， 高斯Copula ， Gibbs采样， 切片采样

1.简介

最近，Copulas作为一种用于计算多变量数据的依赖结构的建模工具而变得流行。

本文的目的是提出一种估计Copula密度函数的贝叶斯非参数方法，审查了copula估算器的参数，半参数和非参数方法。

重点通常放在从某些参数族中选择的copula上。然后通过最大似然估计来执行估计; 伪似然估计。用于估计Copula的半参数和参数方法的比较。 ; 或者通过矩量法或贝叶斯方法，边际分布和模型选择：贝叶斯注记。贝叶斯copula选择。计算统计数据分析。然而，在所有方法中，仍然需要检查依赖结构是否适合于数据，即模型充分性。使用非参数方法获得更灵活的方法，这些方法试图避免特定copula族的假设。

设（X1，Y1），...，（Xn，Yn）是来自未知分布H的随机样本，并且由Fn和Gn表示与F和G样本相关的经验分布函数， 分别。然后Hn（x，y）被认为是经验分布函数，由下式给出

并让相应的经验边际分布函数成为

然后可以获得经验copula函数

这是一个基于秩的copula函数估计。标准化等级（F n（X i），G n（Y i））替换不可观察对（F（X i），G（Y i）），然后形成随机样本（U 1，V 1），...... ，（û ñ，V ñ）从连接函数ç。

还建立了随机向量iid观测的经验copula过程的一致性和渐近正态性。然而，经验copula函数不是连续的，并且需要一些平滑技术来获得使用内核，小波或样条的实际估计器。

2. Copulas和非参数模型

3.吉布斯采样算法

第 1 步：更新w。给定d i，i = 1，...，n的参数的条件分布w j与 ... 成比例其中＃{ d 我 = Ĵ }寄存器的数量d 我，它等于Ĵ和＃{ d 我 > Ĵ }寄存器{的数量d 我 > Ĵ }。

第 2 步：更新z。所述ž 我遵循具有支持均匀分布。

第 3 步：更新d i。d i的值可以位于0和N i之间，其从z i的值导出。我们的密度与d i成正比

第 4 步：更新 ρ。参数ρ的充分条件分布Ĵ给出如下：

其中π（ρ Ĵ）为ρ先验分布Ĵ，我们假定它在与支撑的均匀分布（-1,1）。详细的抽样程序将在稍后讨论。一旦我们可以从中采样，链条完成。

能够从中采样，我们介绍切片采样的想法。将u =Φ（x）和v =Φ（y）代入等式（5），我们可以得到（X，Y），c的依赖结构，其中，Copula密度为

-1 <ρ<1。

然后，完全可能性可以表示为

让和，ρ的后验分布，给定先前的π（ρ），与之成正比

我们以这样的方式引入两个潜在变量λ和η，即后验分布可以表示为

很容易看出整合了潜在变量λ和η，我们将得到ρ的后验分布。现在我们可以使用Gibbs采样器。我们通过模拟ρ~U（-1,1）开始初始化。然后我们使用以下步骤进行更新：

和

在下一节中，我们在一些模拟和真实数据集上运行此代码。

4.数值结果

为了检验所提出的模型的数值性能，我们首先提出两个模拟数据示例。第一个例子有两组，它们是由具有强正相关性的高斯copula生成的，第二个例子来自学生t copula。

对于这些示例中的每一个，我们使用Matlab 生成（U，V）数据集，此处考虑的样本大小为n= 500。将从Gibbs采样器输出（U '，V '）获得的预测数据与生成的数据进行比较。这是基于Gibbs采样器的4000次迭代，并且使用最后的500对，然后使用前3500次迭代的老化时段。通过经典核方法和直方图获得数据和预测样本的双变量copula密度函数估计。

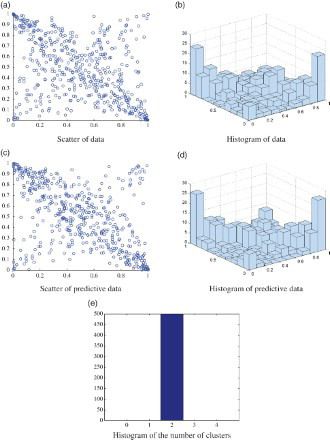
第一个模拟数据模型具有极强的正相关性。选择等式（4）中的高斯copula ，其相关系数为ρ= 0.99。图1中提供了该组数据的四个图形表示。在顶行中，面板（a）和（b）分别显示基于散射和基于内核的copula密度图的生成数据（U，V）。预测样品的那些显示在图（c）和（d）中。

图1.高斯copula，ρ= 0.99，样本大小n = 500。图（a）：数据的散点图; 图（b）：基于内核的copula数据密度; 图（c），（d）和（e）：分别为预测样品的散射，基于核的copula密度和直方图; 图（f）：k的直方图，混合高斯copula密度中的组数。

在这个无限模型中，一个重要的总结是群体或混合物的数量。我们关注有限数量的变量来采样具有正确平稳分布的有效马尔可夫链。每个迭代中的簇数

k在面板（f）中示出。k的平均值为1，这意味着copula密度被认为是一个高斯copula密度。该方法表明，如预期的那样，估计这种类型的copula是非常简单的。

第二个模拟数据模型是学生t copula。图2的面板（a）中的散点图显示了从该copula生成的数据。选择相关系数ρ= -0.5，自由度为ν= 1; 具有低自由度的学生t copula产生更大的上下尾部依赖性（见图2）。预测样品列于图（c）和（d）中。可以看出，预测估计值对真实的copula密度进行了显着的近似。簇（k）的数量如图（e）所示。

图2.学生t copula密度，ρ= -0.5，自由度ν= 1，数字n = 500。图（a）：数据的散点图; 图（b）：数据的直方图; 图（c）和（d）：分别为预测样本的散点图和直方图; 图（e）：k的直方图，混合高斯copula密度中的组数。

最后一个例子使用了一个真实的数据集;

使用MPLE-TV方法分析的类似数据。这里478名受试者提供收缩压（SBP）和舒张压（DBP）血压（mmHg）的测量值。我们通过无限混合模型关注copula估计。在模拟中，让X为SBP和Y.是DBP，所以边缘F（x）和G（y）是未知的。然后我们按照Genest等人的说法。

并考虑观察

这里它表明两种反应之间存在正相关关系，但不是非常强烈。

图3.面板（a）：log（SBP）和log（DBP）的散点图; 图（b）：（log（SBP））/ n和（log（DBP））/ n的等级图。

此处使用的蒙特卡罗样本大小为10,000，初始9000用作老化期（参见图4）。图（c） - （e）中预测样本的图广泛地表征了真实数据的依赖结构。它们使用高斯混合结构在真实数据和我们的预测样本之间显示出强烈的一致性。

图4. SBP和DBP的依赖结构，以及由经验分布函数转换的468对数据。图（a）和（b）：分别为数据的散射和基于核的copula密度图; 图（c） - （e）：分别为预测样本的散射，基于核的copula密度和直方图; 图（f）：k的直方图，混合高斯copula密度中的组数。

在每个迭代中无限模型中的混合物数量k在面板（f）中示出。k的平均值为7.7，这意味着copula密度大致被认为是八个高斯copula密度的混合。这种形状的copula与任何已知的家族模型如Gumbel copula都不相似。

▍需要帮助？联系我们