算法学习：1-1 贪心算法

所谓贪心算法，就是每次操作保证都是局部最优解，以至于最终的结果是全局最优解。

---

455.分发饼干

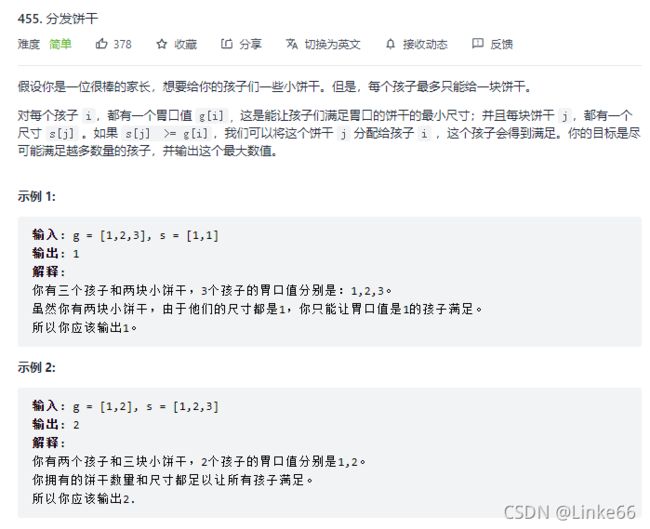
使用贪心算法，关键在于找到贪心策略，即每一步操作都是局部最优解。

本题贪心策略
由题可知，要尽可能满足多的孩子，只要给胃口值最小的孩子分配能让他满足的最小尺寸的饼干，这就是本题的贪心策略。

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        if(g.size()==0||s.size()==0) return 0;  //考虑特殊情况

        sort(g.begin(),g.end());  //按升序排序
        sort(s.begin(),s.end());

        int cnt=0;
        int j=0;
        for(int i=0;i<g.size();){
            if(s[j]>=g[i]){
                //假如饼干尺寸大于等于胃口值
                ++i;
                ++cnt;
            }
            ++j;
            if(j==s.size()) break;
        }

        return cnt;
    }
};

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(),g.end());  //按升序排序
        sort(s.begin(),s.end());

        int child=0,cookie=0;
        while(child<g.size()&&cookie<s.size()){
            if(g[child]<=s[cookie])++child;
            ++cookie;
        }
        return child;
    }
};

---

135.分发糖果

本题贪心策略
我们可以将相邻的孩子中，评分高的孩子必须获得更多的糖果，这句话拆分为两个规则，分别处理。
左规则：当ratings[i-1] 右规则：当rating[i]>rating[i+1]时，i号学生的糖果数量将比i+1的糖果数量多。

解题思路：
1 从左到右走一遍，记录当前点最少需要多少个糖果；
2 从右到左走一遍，记录当前点最少需要多少个糖果；
3 取每个点的最大值，求和就是结果。

class Solution {
public:
    int candy(vector<int>& ratings) {
        int n=ratings.size();
        vector<int>vec(n,0);
        int left=0;
        for(int i=0;i<n;++i){
            if(i>0&&ratings[i]>ratings[i-1]){
                vec[i]=++left;
            }
            else{
                left=1;
                vec[i]=left;
            }
        }

        int right=0,ret=0;
        for(int i=n-1;i>=0;--i){
            if(i<n-1&&ratings[i]>ratings[i+1]){
                ++right;
            }else{
                right=1;
            }
            ret+=max(right,vec[i]);
        }
        return ret;
    }
};

---

452.用最少数量的箭引爆气球

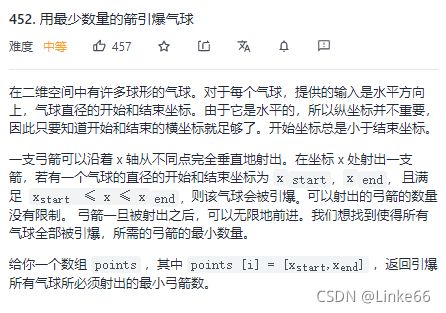
本题贪心策略
先将所有气球，右界按升序排列，那么每次射击右界最小的那个气球就可以了。左界在前面那个右界的右边的气球不会爆，其他都已经爆了，然后再选择没有爆的气球中右界最小的那个。以此类推，就是解决这个问题的最优解。

class Solution {
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        int n=points.size();
        //按右界由小到大排列
        sort(points.begin(),points.end(),
        [](const vector<int>&a,const vector<int>& b){
            return a[1]<b[1];
        });

        int cnt=1;
        int prev=points[0][1];
        for(int i=1;i<n;++i){
            if(points[i][0]>prev){
                ++cnt;
                prev=points[i][1];
            }
        }

        return cnt;
    }
};

---

763.划分字母区间

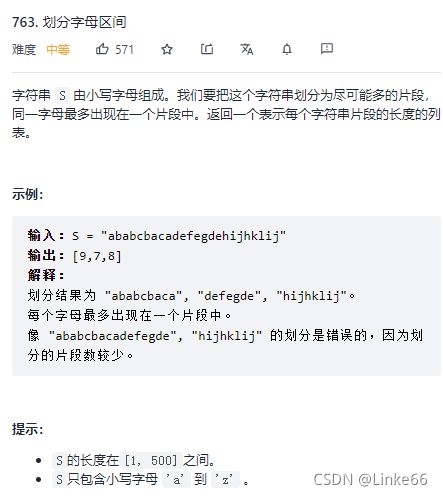
本题贪心策略
记录所有字符的第一次出现时间first，和最后一次出现时间end；
按左界从小到大排序；
left记录当前片段的左界；
pos记录当前片段的右界；

left设置为第一个区间的左界，肯定是0；
pos设置为第一个区间的右界；
进入循环，从第一个区间的下一个区间开始；
假如下一个区间的左界小于pos，那么说明这应该被分在一个片段里，因此更新pos为当前pos和这个区间右界的较大值；
假如下一个区间的右界大于pos，那么说明[left,pos]是一个片段，记录片段长度；更新left为当前区间的左界，pos为当前区间的右界。

class Solution {
public:
    vector<int> partitionLabels(string s) {
        int n = s.size();
        vector<vector<int>>position(26,vector<int>(2,-1));

        unordered_map<char, int>ch_cnt;
        //position记录字符第一次和最后一次出现的下标
        for (int i = 0;i < n;++i) {
            if (ch_cnt[s[i]] == 0)
                position[s[i] - 'a'][0] = i;
            position[s[i] - 'a'][1] = i;
            ++ch_cnt[s[i]];
        }

        //排序，将每个字符出现的区间排序，按左界从小到大排序
        sort(position.begin(), position.end(),
            [](const vector<int>& a, const vector<int>& b) {
                return a[0] < b[0];
            });

        //没出现过的不管
        int i = 0;
        while (i < 26 && position[i][0] == -1)
            ++i;

        vector<int>ret;  //存放结果
        int left = 0;
        int pos = position[i][1]; //记录右界
        for (i = i + 1;i < 26;++i) {
            if (i == 25) {
                if(position[i][0]>pos){
                    ret.push_back(pos - left + 1);
                    ret.push_back(position[i][1]-position[i][0]+1);
                    break;
                }else{
                    pos = max(position[i][1], pos);
                    ret.push_back(pos-left+1);
                }  
            }
            if (position[i][0] < pos) {
                //假如有重合部分
                //更新pos，选取较大的
                pos = max(position[i][1], pos);
            }
            else {
                //没有重合部分
                ret.push_back(pos - left + 1);
                left = position[i][0];
                pos = position[i][1];
            }
        }
        return ret;
    }
};