golang 决策树&随机森林预测

一、Go实现

泰坦尼克生存预测

数据集：train.csv，test.csv  https://www.kaggle.com/c/titanic/data

 

 

package main import ( "fmt" "io/ioutil" "strings" //"strconv" "os" "time" //"math" "github.com/fxsjy/RF.go-master/RF" ) func main() { start := time.Now() f, _ := os.Open("train.csv") defer f.Close() t, _ := os.Open("test.csv") defer t.Close() content, _ := ioutil.ReadAll(f) s_content := string(content) lines := strings.Split(s_content, "\n") inputs := make([][]interface{}, 0) targets := make([]string, 0) for _, line := range lines { line = strings.TrimRight(line, "\r\n") if len(line) == 0 { continue } tup := strings.Split(line, ",") //特征 pattern := tup[:len(tup)-1] //结果 target := tup[len(tup)-1] X := make([]interface{}, 0) for _, x := range pattern { X = append(X, x) } //特征集 inputs = append(inputs, X) //结果集 targets = append(targets, target) } tcontent, _ := ioutil.ReadAll(f) t_content := string(tcontent) tlines := strings.Split(t_content, "\n") tinputs := make([][]interface{}, 0) ttargets := make([]string, 0) for _, line := range tlines { line = strings.TrimRight(line, "\r\n") if len(line) == 0 { continue } tup := strings.Split(line, ",") //特征 pattern := tup[:len(tup)-1] //结果 target := tup[len(tup)-1] X := make([]interface{}, 0) for _, x := range pattern { X = append(X, x) } //特征集 tinputs = append(inputs, X) //结果集 ttargets = append(targets, target) } //训练集 train_inputs := inputs train_targets := targets //测试集 test_inputs := tinputs test_targets := ttargets //构建随机森林 forest := RF.BuildForest(inputs, targets, 10, 500, len(train_inputs[0])) //10 trees test_inputs = train_inputs test_targets = train_targets err_count := 0.0 //测试准确率 for i := 0; i < len(test_inputs); i++ { output := forest.Predicate(test_inputs[i]) expect := test_targets[i] if output != expect { err_count += 1 } } fmt.Println("success rate:", 1.0-err_count/float64(len(test_inputs))) fmt.Println(time.Since(start)) }

 

 

 

测试数据集：car.data

package main import ( "fmt" "io/ioutil" "strings" //"strconv" "os" "time" //"math" "github.com/fxsjy/RF.go-master/RF" ) func main() { start := time.Now() f, _ := os.Open("car.data") defer f.Close() content, _ := ioutil.ReadAll(f) s_content := string(content) lines := strings.Split(s_content, "\n") inputs := make([][]interface{}, 0) targets := make([]string, 0) for _, line := range lines { line = strings.TrimRight(line, "\r\n") if len(line) == 0 { continue } tup := strings.Split(line, ",") //特征 pattern := tup[:len(tup)-1] //结果 target := tup[len(tup)-1] X := make([]interface{}, 0) for _, x := range pattern { X = append(X, x) } //特征集 inputs = append(inputs, X) //结果集 targets = append(targets, target) } train_inputs := make([][]interface{}, 0) train_targets := make([]string, 0) test_inputs := make([][]interface{}, 0) test_targets := make([]string, 0) //将特征集一分为二，一个作为测试集，一个作为训练集 for i, x := range inputs { if i%2 == 1 { test_inputs = append(test_inputs, x) } else { train_inputs = append(train_inputs, x) } } //将结果一分为二，一个作为测试集，一个作为训练集 for i, y := range targets { if i%2 == 1 { test_targets = append(test_targets, y) } else { train_targets = append(train_targets, y) } } //构建随机森林 forest := RF.BuildForest(inputs, targets, 10, 500, len(train_inputs[0])) //10 trees test_inputs = train_inputs test_targets = train_targets err_count := 0.0 //测试准确率 for i := 0; i < len(test_inputs); i++ { output := forest.Predicate(test_inputs[i]) expect := test_targets[i] fmt.Println(output, expect) if output != expect { err_count += 1 } } fmt.Println("success rate:", 1.0-err_count/float64(len(test_inputs))) fmt.Println(time.Since(start)) }

源码及实现：

1.参数说明
inputs 传入特征集
labels 结果集、
treesAmount 树数量（数量越大越准确，但是消耗性能）、
samplesAmount 样本数量（数量越大越准确，但是消耗性能）
selectedFeatureAmount 特征数量
 
func BuildForest(inputs [][]interface{}, labels []string, treesAmount, samplesAmount, selectedFeatureAmount int) *Forest {
   rand.Seed(time.Now().UnixNano())
   forest := &Forest{}
   forest.Trees = make([]*Tree, treesAmount)
   done_flag := make(chan bool)
   prog_counter := 0
   mutex := &sync.Mutex{}
   for i := 0; i < treesAmount; i++ {
      go func(x int) {
         fmt.Printf(">> %v buiding %vth tree...\n", time.Now(), x)
         forest.Trees[x] = BuildTree(inputs, labels, samplesAmount, selectedFeatureAmount)
         //fmt.Printf("<< %v the %vth tree is done.\n",time.Now(), x)
         mutex.Lock()
         prog_counter += 1
         fmt.Printf("%v tranning progress %.0f%%\n", time.Now(), float64(prog_counter)/float64(treesAmount)*100)
         mutex.Unlock()
         done_flag <- true
      }(i)
   }

   for i := 1; i <= treesAmount; i++ {
      <-done_flag
   }

   fmt.Println("all done.")
   return forest
}
 
 
2.主要是这段逻辑，去构建决策树
 forest.Trees[x] = BuildTree(inputs, labels, samplesAmount, selectedFeatureAmount)
 
3.BuildTree
 
inputs 传入特征集
labels 结果集、
samplesAmount 样本数量（数量越大越准确，但是消耗性能）
selectedFeatureAmount 特征数量


func BuildTree(inputs [][]interface{}, labels []string, samples_count,selected_feature_count int) *Tree{

   samples := make([][]interface{},samples_count)
   samples_labels := make([]string,samples_count)
   //1.离散样本
   for i:=0;i 
  
 
4.buildTree
 
这部分是关键代码，首先是选取最优属性，即纯度最高的特征，这时候要用过“信息熵（information entropy）”
信息熵的定义：假如当前样本集D中第k类样本所占的比例为， 为类别的总数（对于二元分类来说，）。则样本集的信息熵为：
 
  
 
  
pk越大，pklog2pk越大，累积求和Ent(D)越小，当只有一个样本的时候，Pk=1，log2Pk=0,信息熵为0
 
  
 
 
  
  Ent(D)越小，D的纯度越高。   然后有了信息熵以后就可以求信息增益，信息增益是假定离散属性 有 个可能的取值，如果使用特征  来对数据集D进行划分，则会产生V个分支结点， 其中第v个结点包含了数据集D中所有在特征  上取值为 的样本总数，记为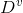。因此可以根据上面信息熵的公式计算出信息熵，再考虑到不同的分支结点所包含的样本数量不同，给分支节点赋予权重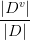，即样本数越多的分支节点的影响越大，因此，能够计算出特征  对样本集D进行划分所获得的“信息增益”:
 
  
 
  
  一般而言，信息增益越大，则表示使用特征  对数据集划分所获得的“纯度提升”越大。所以信息增益可以用于决策树划分属性的选择，其实就是选择信息增益最大的属性，ID3算法就是采用的信息增益来划分属性。
 
  
 
 
  
总之，就是选取信息增益最大的特征作为树的根结点，如果该节点只包含一个样本，就无须继续划分，直接将结果（生存或者死亡）作为叶子节点，否则就继续递归划分属性。
 
  
详情可以参考：https://blog.csdn.net/u012328159/article/details/70184415
 
  
 
 
  
samples 传入特征集 
 
  
samples_labels 结果集 
 
  
selected_feature_count 特征数量 
 
  
 
 
  
 
 
  
 
   
 
    
 
     
 
func buildTree(samples [][]interface{}, samples_labels []string, selected_feature_count int) *TreeNode{
   //fmt.Println(len(samples))
   //find a best splitter
   column_count := len(samples[0])
   //split_count := int(math.Log(float64(column_count)))
   split_count := selected_feature_count
   //离散列数据
   columns_choosen := getRandomRange(column_count,split_count)
   
   best_gain := 0.0
   var best_part_l []int = make([]int,0,len(samples))
   var best_part_r []int = make([]int,0,len(samples))
   var best_total_l int = 0 
   var best_total_r int = 0
   var best_value interface{}
   var best_column int
   var best_column_type string
    //获取正反例数量
   current_entropy_map := make(map[string]float64)
   for i:=0;i=best_gain{
         best_gain = gain
         best_value = value
         best_column = c
         best_column_type = column_type
         best_total_l = total_l
         best_total_r = total_r
      }
   }
   if best_gain>0 && best_total_l>0 && best_total_r>0 {
      node := &TreeNode{}
      node.Value = best_value
      node.ColumnNo = best_column
      splitSamples(samples, best_column_type, best_column, best_value,&best_part_l,&best_part_r)
      //选择最好的分支继续递归
      node.Left = buildTree(getSamples(samples,best_part_l),getLabels(samples_labels,best_part_l), selected_feature_count)
      node.Right = buildTree(getSamples(samples,best_part_r),getLabels(samples_labels,best_part_r), selected_feature_count)
      return node
   }
      
   return genLeafNode(samples_labels)
   
}
 
 
    
 
   
 
  
 
  
 
 
  
 
 
  
二、借助RedisML实现