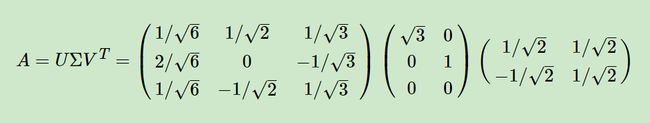主成分分析 PCA（Principal Component Analysis）学习笔记

学习目标

掌握主成分分析的基本原理、公式推导和具体的实现

---

1. PCA的基本原理

PCA（Principal Component Analysis）即为一种降维操作，本质上就是基的变换，论文1¹中列出了PCA的几个主要作用：

• Simplification Model
• Data Reduction
• Variable selection
• Reduce Noise

特别多的应用在了较为复杂的模型中，用于挑选变量，简化掉一些对最终结果贡献比较小的变量（这些变量可以看作噪音或者冗余），使得挑选后的每个特征都是相互独立的（线性无关），表现在每个维度的基坐标相互垂直（即正交基）

2.PCA的基本公式推导

PCA的目标是使各个点在变换后的基坐标上的投影之和最大，从几何意义上理解，就是使得各个点在变换后的坐标系上分布的最为分散。这也就是《机器学习》²中提到的最大可分性。

2.1 去中心化

在进行主成分分析之前需要对数据点进行去中心化，即每个点在某一维度的值减去该维度的平均值。

$\bar{x}：\frac{1}{n}{\sum }_{i=0}^n{x}_i$

去中心化后：$x_i=x_i-\bar{x}$

为什么要进行中心化？

最主要的是为了更方便的计算协方差

计算协方差的公式：

协方差 = $\frac{1}{n-1}$${\sum }_{i=0}^n(x_i-\bar{x})(y_i-\bar{y})$

在进行中心化过后，不需要再多次计算$(x_i-\bar{x})$和$(y_i-\bar{y})$的值，提高了计算的效率

其次是为了使数据更加规整，让原本比较凌乱的数据有了关系，可以更方便的观察到哪个是主成分，哪个不是主成分

去中心化后也可以对数据进行标准化:

0-1法：$x_i$=$\frac{x_i-min}{max-min}$

z-score法：$x_i$=$\frac{(x_i-\mu )}{\sigma }$

标准化的目的主要是为了统一变量的量纲，如有些变量1为kg，变量2为长度cm，可能cm的值要比kg大很多，这就有可能使最后的结果产生偏差。标准化的意义就在于可以使得这些变量可以在同一个起点（平台）上进行比较。

2.2 分解特征值法求解主成分

2.2.1 求解数据的协方差

为什么会想到使用到协方差？

上节中说，我们的目标是寻找使得数据d最为分散的基。而在数学中常用到方差来表示数据的混乱程度，在高维空间中常使用协方差来描述两个变量之间的关系

求解协方差的公式如下：

$corr$ = $\frac{1}{n-1}$${\sum }_i^n(x_i-\bar{x})(y_i-\bar{y})$

协方差矩阵可以表示为：

$CORR$ = $\left(\begin{array}{cc}COV(X,X)& COV(X,Y)\\ COV(Y,X)& COV(Y,Y)\end{array}\right)$

可以看出，在 $X$ 已经去中心化的基础上，协方差的值可以直接等价于

$\frac{1}{n-1}X{X}^T$

2.2 寻找目标函数

前面说过寻找主成分的方法就是寻找一个新的基（坐标），使得数据点在该坐标上的分布最为分散（这样重叠/相互影响的值就会越少），投影值最大（应该也可以从熵的角度理解，熵越大，越分散，包含的信息量越多）。

在$s$上的投影值可以表示为

$s$ = $u\cdot a$

其中$u$表示$s$方向上的单位向量，$a$为数据点

到原点的距离可以表示为 $s^2$，那么我们的目标函数就是求解$max{s}^2$

$max$$s^2$=$\frac{1}{n-1}{\sum }_i^n{s}^2$

=${\sum }_i^n\frac{u\cdot a\cdot u\cdot a}{n-1}$

=$\frac{u\cdot X\cdot X^T\cdot u}{n-1}$

前面我们说协方差的公式为

$C=$$\frac{1}{n-1}X{X}^T$

因此上式可以转化为:

$max{s}^2$=$u\cdot C\cdot u^T$

如何判断该式子是否存在极值呢？应该判断矩阵$C$是否为半正定矩阵。

判断半正定矩阵的两个条件：

1.该矩阵为实对称矩阵
2.该矩阵的特征值均大于等于0

针对条件1：$(X{X}^T{)}^T$=$(X{X}^T)$，因此为实对称矩阵
针对条件2：$X{X}^T\varphi$=$\lambda$ $\varphi$

$(X{X}^T\varphi {)}^T$$\varphi$=($\lambda$$\varphi$)${}^T$$\varphi$
${\varphi }^{T}X{X}^T\varphi$=$\lambda {\varphi }^T\varphi$
$(X^T\varphi {)}^T$$(X^T\varphi )$=$\lambda {\varphi }^2$
$(X^T\varphi {)}^2$=$\lambda {\varphi }^2$

因此$\lambda$大于等于0，即特征值大于等于0
因此$s^2$为半正定矩阵的二次型，存在极值

2.3 利用拉格朗日数乘法求解极值（特征值分解法）

之前学了SVM模型中可以使用拉格朗日数乘法求解距最优超平面的距离的极值，同样也可以将拉格朗日数乘法应用在PCA中，求解投影的极值

$max{s}^2$=$u\cdot C\cdot u^T$ $s.t.$ $u\cdot u^T$=1

转化为：

max $s^2$=$u\cdot C\cdot u^T$ -$\lambda$$(1-u\cdot u^T)$

求导：

$2uC$-$2\lambda u$=0
即：$C$=$\lambda$

求特征值$\lambda$ (求解方法详见线性代数同济版最后一章）：

$|C-\lambda E|$$=0$

其中$E$为单位矩阵

也就是说 最大的$s^2$ = 特征值$\lambda$

在进行降维时，可以选择排在前面的特征值$\lambda$（等价于选择了分布最为分散的几个基坐标）

根据特征值与特征向量之间的关系求出对应的特征向量$\varphi$

公式：$(C-\lambda E)\varphi =0$

变换到新基下面的新坐标 = 旧坐标 * 特征向量

这样就达到了换基的目的，实现了降维

举个栗子：

现在有去中心化后的数据：

$\left(\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right)$

我们求解其协方差：
$C$=$\frac{1}{5}$$\left(\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right)$$\left(\begin{array}{cc}-1& -2\\ -1& 0\\ 0& 0\\ 2& 1\\ 0& 1\end{array}\right)$

=$\frac{1}{5}$$\left(\begin{array}{cc}6& 4\\ 4& 6\end{array}\right)$

=$\left(\begin{array}{cc}\frac{6}{5}& \frac{4}{5}\\ \frac{4}{5}& \frac{6}{5}\end{array}\right)$

求出来协方差之后再求解其特征值：

$|C-\lambda E|=0$

$\left(\begin{array}{cc}\frac{6}{5}& \frac{4}{5}\\ \frac{4}{5}& \frac{6}{5}\end{array}\right)$-$\left(\begin{array}{cc}\lambda & 0\\ 0& \lambda \end{array}\right)$=$\left(\begin{array}{cc}\frac{6}{5}-\lambda & \frac{4}{5}\\ \frac{4}{5}& \frac{6}{5}-\lambda \end{array}\right)$

这样可以得到：

$(\frac{6}{5}-\lambda {)}^2$-$(\frac{4}{5}{)}^2$=0

$(5\lambda -2)(\lambda -2)=0$

$\lambda =\frac{2}{5}$,$2$

如果想要降到k维的话，可以选择最大的k个$\lambda$，这里我们将其降到1维，选择最大的一个$\lambda$，也就是2

根据 $\lambda$ 我们可以求出对应的特征向量，代入$\lambda$

$(C-\lambda E)X=0$

$\left(\begin{array}{cc}\frac{-4}{5}& \frac{4}{5}\\ \frac{4}{5}& \frac{-4}{5}\end{array}\right)$$\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)$=0

解得$x_1=1,x_2=1$，这时我们得到了特征向量 $\left(\begin{array}{c}1\\ 1\end{array}\right)$

因为标准基的模为1，所以我们将其转化为

$\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right)$

以特征向量作为新的基，将我们的旧坐标以新的基为底，换成新坐标

$\left(\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right)$$\left(\begin{array}{ccccc}-1& -1& 0& 2& 0\\ -2& 0& 0& 1& 1\end{array}\right)$

=$\left(\begin{array}{ccccc}\frac{-3}{\sqrt{2}}& \frac{-1}{\sqrt{2}}& 0& \frac{3}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right)$

这样就实现了新坐标与旧坐标之间的转化

参考《机器学习》²，总结一下PCA降维的过程：

2.4 SVD（奇异值分解法）

奇异值分解指的是矩阵$X$可以分解成：

$X=u\sum v^T$

其中$X$是$m\ast n$的矩阵(即我们的原始数据,可以为非方阵），$u$ 为$m\ast m$的矩阵（为$X{X}^T$的特征向量），$\sum$ 为$m\ast n$的矩阵(为$X{X}^T$或者$X^{T}X$的奇异矩阵），$v$为n*n的矩阵（为$X^{T}X$的特征向量）

证明：

$X{X}^T$=$u\sum v^T$*$(u\sum v^T{)}^T$

=$u\sum v^T$*$(v{\sum }^T{u}^T)$

=$u{\sum }^2{u}^T$

根据线性代数的知识可以得到

矩阵$X$=其特征向量$Q$ * 该矩阵的特征值 * 特征向量$Q^T$

因此$X=u\sum v^T$符合该式子，故成立

按照该方法我们可以分解出矩阵$A$的奇异值，奇异值^2即为特征值（上式已经证明），根据特征向量即可求出对应的新坐标 ³

注意到我们的SVD也可以得到协方差矩阵最大的k个特征向量张成的矩阵，但是SVD有个好处，有一些SVD的实现算法可以不求先求出协方差矩阵，也能求出我们的右奇异矩阵V。也就是说，我们的PCA算法可以不用做特征分解，而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是我们我们认为的暴力特征分解。

SVD的步骤：

1.求$X{X}^T$的特征向量和特征值，构成$U$
2.求$X^{T}X$的特征向量和特征值 ，构成$V$
3.求$X^{T}X$的特征值的平方根（即奇异值），构成$\sum$

举个栗子：

我们对$A$矩阵进行分解:

$A$=$\left(\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right)$

$A^T$=$\left(\begin{array}{ccc}0& 1& 1\\ 1& 1& 0\end{array}\right)$

1.先求出$A{A}^T$和$A^{T}A$：

$A{A}^T$=$\left(\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right)$*$\left(\begin{array}{ccc}0& 1& 1\\ 1& 1& 0\end{array}\right)$

=$\left(\begin{array}{ccc}1& 1& 0\\ 1& 2& 1\\ 0& 1& 1\end{array}\right)$

$A^{T}A$=$\left(\begin{array}{ccc}0& 1& 1\\ 1& 1& 0\end{array}\right)$*$\left(\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right)$

=$\left(\begin{array}{cc}2& 1\\ 1& 2\end{array}\right)$

2.选取$A{A}^T$的特征值和特征向量:

$A{A}^T$=$\left(\begin{array}{ccc}1& 1& 0\\ 1& 2& 1\\ 0& 1& 1\end{array}\right)$-$\left(\begin{array}{ccc}\lambda & 0& 0\\ 0& \lambda & 0\\ 0& 0& \lambda \end{array}\right)$

=$\left(\begin{array}{ccc}1-\lambda & 1& 0\\ 1& 2-\lambda & 1\\ 0& 1& 1-\lambda \end{array}\right)$

=$(1-\lambda )(2-\lambda )(1-\lambda )-(1-\lambda )-(1-\lambda )$

解得$\lambda$=0,1,3

$\lambda$=3时：

特征向量为：$\left(\begin{array}{ccc}\&1& 0& \\ 1& 2& 1\\ 0& 1& 1\end{array}\right)$

$\lambda$=1时：
特征向量为：$\left(\begin{array}{ccc}1& 1& 0\\ 1& 2& 1\\ 0& 1& 1\end{array}\right)$

$\lambda$=0时：
特征向量为：$\left(\begin{array}{ccc}1& 1& 0\\ 1& 2& 1\\ 0& 1& 1\end{array}\right)$

3.选取$A^{T}A$的特征值和特征向量:

$\left(\begin{array}{cc}2& 1\\ 1& 2\end{array}\right)$-$\left(\begin{array}{cc}\lambda & 0\\ 0& \lambda \end{array}\right)$=$\left(\begin{array}{cc}2-\lambda & 1\\ 1& 2-\lambda \end{array}\right)$

即：$(2-\lambda )$*$(2-\lambda )$-1=0
即：3-4$\lambda$+${\lambda }^2$=0

即：${\lambda }_1=3$，${\lambda }_2=1$

${\lambda }_1=3$时：

$\left(\begin{array}{cc}-1& 1\\ 1& -1\end{array}\right)$*$\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)$=0

即 $x_1=x_2=1$，即特征向量为$\left(\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right)$

${\lambda }_2=1$时：

$\left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right)$*$\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)$=0

特征向量为$\left(\begin{array}{c}\frac{-1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right)$

奇异值为$\sqrt{{\lambda }_i}$，可以解出$\sqrt{3}$和$1$

所以矩阵A可以分解为：

2.5.SVD用于PCA

上一节中，我们讲到要用PCA降维，需要找到样本协方差矩阵$X^{T}X$的最大的$d$个特征向量，然后用这最大的$d$个特征向量张成的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵$X^{T}X$，当样本数多样本特征数也多的时候，这个计算量是很大的⁴。

其实在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵：

$A_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}V{T}_{n\times n}\approx U_{m\times k}{\Sigma }_{k\times k}V{T}_{k\times n}$

按照这种方法将SVD应用在PCA中

二者本质上都是对$X{X}^T$矩阵进行特征的分解，求其特征向量，进行坐标映射。

3.PCA的性质

1.PCA能够筛选特征与降噪（信号领域），并且在一定程度上避免了维度灾难
2.PCA相当于浓缩了对模型结果比较重要的信息，在一定程度上会造成一定的过拟合
3.PCA降维后的可表示性不强，降维过后的值或许只有计算机可以理解他的真正意义…

3.实战

使用鸢尾花的数据集对其进行了PCA降维

按照方法1（直接分解特征值）：

导包

import numpy as np
from sklearn import datasets

导入数据集

data=np.genfromtxt('iris.data.txt',delimiter=',')

进行去中心化处理

x=data[:,:4]
for j in range(0,x.shape[1]):
    x[:,j]=[i-np.mean(x[:,j]) for i in x[:,j]]

求解协方差

C=((x.T).dot(x))/(x.shape[0]-1)

求解特征值和特征向量

eig_paris=np.linalg.eig(C)

print(eig_vals)
print(eig_vecs)

选取最大的两个特征值对应的特征向量

w=eig_vecs[:,:3]
pca_character=data[:,:4].dot(w)

下面看一下在回归问题中，PCA的降维后会产生什么变化

导包

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
from sklearn.model_selection import StratifiedKFold

这是未经过PCA降维的回归，结果如下

kf=StratifiedKFold(5)  //5折交叉验证
character=data[:,:4]
label=data[:,-1]
for (train,test) in kf.split(character,label): 
	model=LogisticRegression()
	model.fit(character[train],label[train])
	result=model.predict(character[test])
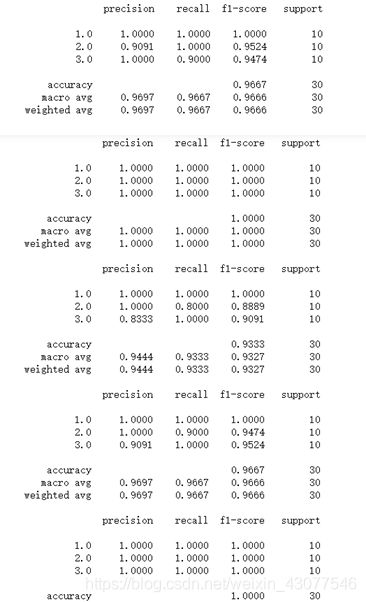
	print(classification_report(label[test],result,digits=4))

使用PCA降维后的数据：

for (train,test) in kf.split(pca_character,label): 
	model=LogisticRegression()
	model.fit(pca_character[train],label[train])
	result=model.predict(pca_character[test])
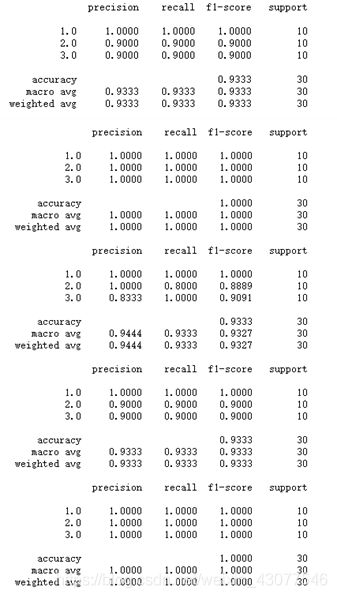
	print(classification_report(label[test],result,digits=4))

结果如下：

运行时间：

使用方法二（SVD降维）：

#采用婴尾花的数据集、
import numpy as np
from sklearn import datasets
import datetime
data=np.genfromtxt('iris.data.txt',delimiter=',')
kf=StratifiedKFold(5)
x=data[:,:4]
for j in range(0,x.shape[1]):
    x[:,j]=[i-np.mean(x[:,j]) for i in x[:,j]]
#.dot函数：如果是两个vector返回的是两个向量的内积，如果是矩阵相乘，则返回的是线性代数那样的乘法
C=((x.T).dot(x))/(x.shape[0]-1)
#计算特征值和特征向量
old=datetime.datetime.now()
[u,s,v]=np.linalg.svd(x)   #特征矩阵按照特征值降序排列
new=datetime.datetime.now()
print("运行时间：",new-old)
print("xxt特征矩阵",v)
print("xtx特征矩阵",u)
svd_character=x.dot(v.T[:,:2])
label=data[:,-1]

for (train,test) in kf.split(svd_character,label):   #进行分层抽样
    model=LogisticRegression()
    model.fit(svd_character[train],label[train]) 
    result=model.predict(svd_character[test]) 
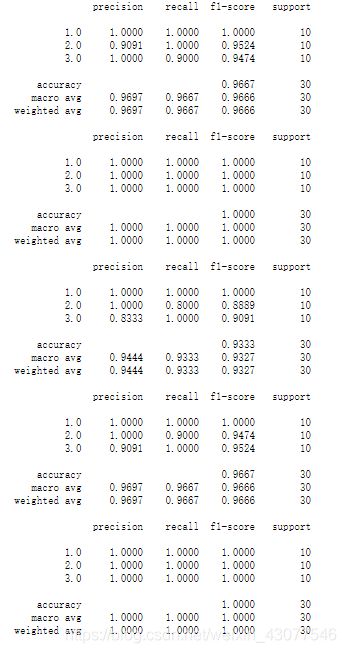
    print(classification_report(label[test],result,digits=4))

SVD的运行时间：

1.降维后和未经过降维的结果相比下降了一些，但没有很大的变化
2.SVD的运行时间比PCA特征分解的时间少了很多，在数据量大的数据集上表现得应该更明显

这里需要注意一下的是：
1.np.linalg.eig和np.linalg.svd求出的特征矩阵并不是完全一样的，是相互转置的关系np.linalg.eig求出的特征矩阵的列，对应一个特征值；而np.linalg.svd求出的特征矩阵的行，对应一个特征值,所以需要对np.linalg.svd求出的特征矩阵进行转置，再与原来的坐标进行.dot
2.在np.linalg.eig中,求出的特征值并不是按照降序排列，因此可以对矩阵先进行归一化，观察对角线上特征值的大小，再选择对应的特征向量

参考文献：

---

1. PCA——Principal components analysis ↩︎

2. 《机器学习》 周志华 ↩︎ ↩︎

3. 机器学习——PCA降维(我至今为止遇见的最好的博文) ↩︎

4. 奇异值分解(SVD)原理与在降维中的应用 ↩︎