【智能优化算法】基于全局优化的改进鸡群算法求解单目标优化问题(ECSO)附matlab代码
1 简介
智能算法分为两种,一种是群体智能算法(swarmintelligencealgorithm),该算法大多模拟自然界中动植物的特有行为,并将其表达成数学语言,从而进行迭代寻优,如模拟蝙蝠回声定位行为而提出的蝙蝠算法(batalgorithm,BA)和模拟大杜鹃巢寄卵生特性的布谷鸟搜索算法(cuckoosearchalgorithm,CS)[2];另一种是进化算法,如差分进化算法(differentialevolution,DE)是一种基于群体差异性的寻优算法,通过变异、交叉、选择的操作来进行迭代寻优。这些算法促进了计算科学的发展。根据 NFL定理,不存在某种算法在全部优化领域都存在优势,因此,近年来便有多种智能算法被提出,用于弥补已有算法的不足。鸡群优化算法(chickenswarmoptimization,CSO)是由 Meng等人[4]于 2014年提出,其模拟鸡群中的等级区分制度和群体行为,将鸡群种群划分为公鸡、母鸡和小鸡,不同的种群进行不同的移动策略,等级区分下特定种群中依然存在着竞争,这种根据不同的种群而制定不同的寻优策略有利于保持种群的竞争性。CSO已被证明在函数优化领域优于粒子群算法,并且已经成功应用于工程优化设计问题、多分类器系数优化和聚类分析,这些成功的应用案例表明了 CSO拥有较好的应用前景。
在基本鸡群算法的基础上提出了一种改进版鸡群算法(ECSO),在公鸡位置的更新过程中引入自适应变异策略用于平衡算法迭代后期下降的种群多样性,提升收敛速度;在母鸡移动过程中引入偏好随机游动策略来平衡算法的开发与探索阶段,增强算法的稳定性;在小鸡位置更新时引入领导者策略,减少算法搜索的盲目性;最后,通过测试多组函数,并与基本蝙蝠算法和鸡群算法以及已有改进的鸡群算法进行对比,验证了改进算法的有效性.
2 部分代码
% -----------------------------------------------------------------------------------------------------------% Chicken Swarm Optimization (CSO) (demo)% Programmed by Xian-bing Meng% Updated 25 Aug, 2014.%% This is a simple demo version only implemented the basic% idea of the CSO for solving the unconstrained problem, namely Sphere function.% The details about CSO are illustratred in the following paper.% (Citation details):% Xian-bing Meng, Xiao-zhi Gao., A new bio-inspired algorithm: Chicken Swarm Optimization% in: ICSI 2014, Part I, LNCS 8794, pp. 86-94% Email: x.b.meng12@gmail.com; xiao-zhi.gao@aalto.fi%% The parameters in CSO are presented as follows.% fitness % The fitness function% M % Maxmimal generations (iterations)% pop % Population size% dim % Number of dimensions% G % How often the chicken swamr can be updated.% rPercent % The population size of roosters accounts for "rPercent" percent of the total population size% hPercent % The population size of hens accounts for "hPercent" percent of the total population size% mPercent % The population size of mother hens accounts for "mPercent" percent of the population size of hens%% Using the default value, you can execute this algorithm using the following code.% [ bestX, fMin ] = CSO% -----------------------------------------------------------------------------------------------------------% Main programs starts herefunction [ bestX, fMin ] = CSO( fitness, M, pop, dim, G, rPercent, hPercent, mPercent )% Display helphelp CSO.m%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% set the parameter valuesif nargin < 1Func = @Sphere;M = 1000; % Maxmimal generations (iterations)pop = 100; % Population sizedim = 20; % Number of dimensionsG = 10; % How often the chicken swamr can be updated. The details of its meaning are illustrated at the following codes.rPercent = 0.2; % The population size of roosters accounts for "rPercent" percent of the total population sizehPercent = 0.6; % The population size of hens accounts for "hPercent" percent of the total population sizemPercent = 0.1; % The population size of mother hens accounts for "mPercent" percent of the population size of hensend%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%rNum = round( pop * rPercent ); % The population size of roostershNum = round( pop * hPercent ); % The population size of henscNum = pop - rNum - hNum; % The population size of chicksmNum = round( hNum * mPercent ); % The population size of mother henslb= -100*ones( 1,dim ); % Lower limit/bounds/ a vectorub= 100*ones( 1,dim ); % Upper limit/bounds/ a vector%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%Initializationfor i = 1 : popx( i, : ) = lb + (ub - lb) .* rand( 1, dim ); % The position of the i (th) chickenfit( i ) = Func( x( i, : ) ); % The fitness value of the i (th) chickenendpFit = fit; % The individual's best fitness valuepX = x; % The individual's best position corresponding to the pFit[ fMin, bestI ] = min( fit ); % fMin denotes the global optimum fitness valuebestX = x( bestI, : ); % bestX denotes the global optimum position corresponding to fMin%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Start updating the solutions.for t = 1 : M% This parameter is to describe how the chicks would follow their mother to forage for food.FL = rand( pop, 1 ) .* 0.4 + 0.5; % In fact, there exist cNum chicks, thus only cNum values of FL would be used.%Note that cNum may be dynamically changed!% The hierarchal order, dominance relationship, mother-child relationship, the roosters, hens and the chicks in a% group will remain unchanged. These statuses are only updated every several ( G) time steps.% In fact, this parameter G is used to simulate the situation that the chicken swarm have been changed, including that some% chickens have died, or the chicks have grown up and became roosters or hens,% or some mother hens have hatched new offspring (chicks) and so on.if( mod( t, G ) == 1 )sortIndex = ones( pop, 1 ) .* ( pop + 1 ); % Initialize the sortIndex, the values of which would be anything valid.% Except the ones that are the indexs of the chicken, such as 1,2,3,……pop.[ ans, sortIndex ] = sort( fit ); % Here ans would be unused. Only sortIndex is useful.% Note that how the chicken swarm can be divided into several groups and the identity% of the chickens (roosters, hens and chicks) can be determined all depend on the fitness values of the% chickens themselves. Hence we use " sortIndex( i ) " to describe the% chicken, not the index " i " itself.motherLib = randperm( hNum, mNum ) + rNum; % Randomly select which mNum hens would be the mother hens.% We assume that all roosters are stronger than the hens, likewise, hens are stronger than the chicks.% In CSO, the strong is reflected by the good fitness value. If the% optimization problems is minimal ones, the more strong ones% correspond to the ones with lower fitness values.% Hence 1 : rNum chickens all belong to roosters.% In turn, (rNum + 1) : (rNum + 1 + hNum ) belong to hens, .....chicks% Here motherLib include all the mother hens.% motherLib is the abbreviation of "mother library".% Given the fact the 1 : rNum chickens' fitness values maybe not% the best rNum ones.% Thus we use sortIndex( 1 : rNum ) to describe the roosters.mate = randi( rNum, hNum, 1 ); % randomly select each hen's mate, rooster.% In fact, we can determine which group each hen inhabit using "mate"% Each rooster stands for a group.For simplicity, we assume that% there exist only one rooster in each group.mother = motherLib( randi( mNum, cNum, 1 ) ); % randomly select cNum chicks' mother hensend%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%for i = 1 : rNum % Update the rNum roosters' values.anotherRooster = randiTabu( 1, rNum, i, 1 ); % randomly select another rooster different from the i (th) chicken.if( pFit( sortIndex( i ) ) <= pFit( sortIndex( anotherRooster ) ) )tempSigma = 1;elsetempSigma = exp( ( pFit( sortIndex( anotherRooster ) ) - pFit( sortIndex( i ) ) ) / abs( pFit( sortIndex( i ) ) + 1e-50 ) );endx( sortIndex( i ), : ) = pX( sortIndex( i ), : ) .* ( 1 + tempSigma .* randn( 1, dim ) );x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );fit( sortIndex( i ) ) = Func( x( sortIndex( i ), : ) );endfor i = ( rNum + 1 ) : ( rNum + hNum ) % Update the hNum hens' values.other = randiTabu( 1, i, mate( i - rNum ), 1 ); % randomly select another chicken different from the i (th) chicken's mate.% Note that the "other" chicken's fitness value should be superior% to that of the i (th) chicken. This means the i (th) chicken may steal% the better food found by the "other" (th) chicken.c1 = exp( ( pFit( sortIndex( i ) ) - pFit( sortIndex( mate( i - rNum ) ) ) ) / abs( pFit( sortIndex( i ) ) + 1e-50 ) );c2 = exp( ( -pFit( sortIndex( i ) ) + pFit( sortIndex( other ) ) ) );x( sortIndex( i ), : ) = pX( sortIndex( i ), : ) + ( pX( sortIndex( mate( i - rNum ) ), : ) - pX( sortIndex( i ), : ) ) .* c1 .* rand( 1, dim ) +...( pX( sortIndex( other ), : ) - pX( sortIndex( i ), : ) ) .* c2 .* rand( 1, dim );x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );fit( sortIndex( i ) ) = Func( x( sortIndex( i ), : ) );endfor i = ( rNum + hNum + 1 ) : pop % Update the cNum chicks' values.x( sortIndex( i ), : ) = pX( sortIndex( i ), : ) + ( pX( sortIndex( mother( i - rNum - hNum ) ), : ) - pX( sortIndex( i ), : ) ) .* FL( i );x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );fit( sortIndex( i ) ) = Func( x( sortIndex( i ), : ) );end%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Update the individual's best fitness vlaue and the global best fitness valuefor i = 1 : popif ( fit( i ) < pFit( i ) )pFit( i ) = fit( i );pX( i, : ) = x( i, : );endif( pFit( i ) < fMin )fMin = pFit( i );bestX = pX( i, : );endendend% End of the main program%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% The following functions are associated with the main program%---------------------------------------------------------------------------------------------------------------------------% Note that this function is the objective functionfunction y = Sphere( x )y = sum( x .^ 2 );% Application of simple limits/boundsfunction s = Bounds( s, Lb, Ub)% Apply the lower bound vectortemp = s;I = temp < Lb;temp(I) = Lb(I);% Apply the upper bound vectorJ = temp > Ub;temp(J) = Ub(J);% Update this new moves = temp;%---------------------------------------------------------------------------------------------------------------------------% Note that this function generate "dim" values, all of which are% different from the value of "tabu"function value = randiTabu( min, max, tabu, dim )value = ones( dim, 1 ) .* max .* 2;num = 1;while ( num <= dim )temp = randi( [min, max], 1, 1 );if( length( find( value ~= temp ) ) == dim && temp ~= tabu )value( num ) = temp;num = num + 1;endend%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
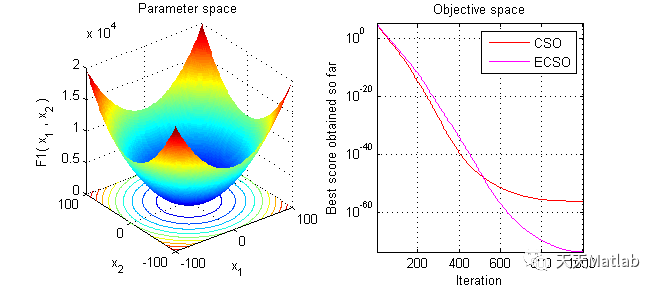
3 仿真结果
4 参考文献
[1]韩斐斐, 赵齐辉, 杜兆宏,等. 全局优化的改进鸡群算法[J]. 计算机应用研究, 2019, 36(8):4.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。