机器学习——逻辑回归(分类算法)、聚类算法
目录
模型的保存与加载
逻辑回归——能得出概率值
逻辑回归的损失函数、优化
sklearn逻辑回归API
LogisticRegression回归案例——良/恶性乳腺癌肿瘤预测
pandas使用
分类流程
LogisticRegression回归案例——上下文点击
LogisticRegression总结
多分类问题
生成模型和判别模型
无监督学习——K-means
k-means步骤
k-means API
Kmeans性能评估指标
API
总结
![]()
模型的保存与加载
from sklearn,externals import joblib
joblib.dump(rf,'test.pkl')——保存
estimator = joblib.load('test.pkl')——加载
#### 保存训练好的模型
joblib.dump(lr,'./tmp/test.pkl')
#### 预测房价结果
model = joblib.load('./tmp/test.pkl')
y_predict = std_y.inverse_transform(model.predict(x_test))
print('保存的模型预测的结果:',y_predict)逻辑回归——能得出概率值
线性回归的式子作为逻辑回归的输入
应用:预测广告点击率
逻辑回归是解决二分类问题的利器
输入:
![]() ——单个样本
——单个样本
逻辑回归公式:
![]()
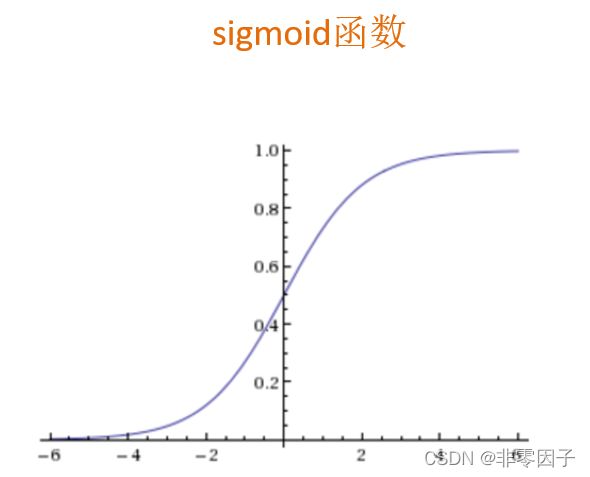
输出:[0,1]区间的概率值,默认0.5为阀值
g(z)为sigmoid函数——[0,1],z等于回归的结果
逻辑回归的损失函数、优化
与线性回归原理相同,但由于是分类问题,损失函数不一样,只能通过梯度下降求解
逻辑回归只会判断属于某一个类别的概率,相对就自然知道属于另一个类别的概率
| 样本 | 阈值 | 分类 | |
| 1 | 0.65 | 0.55 | 1 |
| 2 | 0.51 | 0 | |
| 3 | 0.32 | 0 | |
| 4 | 0.73 | 1 |
四个损失值相加:(可看作信息熵,但不是信息熵)——对数似然损失
![]()
用梯度下降进行优化
损失函数:——尽管没有全局最低点,但是效果都是不错的
均方误差——只有一个最小值(不存在多个局部最低点)
对数似然损失——多个局部最小值(目前解决不了)
尽量改善方案:
1、多次随机初始化,多次比较最小值结果
2、求解过程当中,调整学习率
sklearn逻辑回归API
sklearn.linear_model.LogisticRegression(penalty(正则化)=‘l2’, C = 1.0)
Logistic回归分类器
coef_:回归系数
LogisticRegression回归案例——良/恶性乳腺癌肿瘤预测
原始数据的下载地址:
Index of /ml/machine-learning-databases/breast-cancer-wisconsin
数据描述
(1)699条样本,共11列数据,第一列用语检索的id,后9列分别是与肿瘤相关的医学特征,最后一列表示肿瘤类型的数值。
(2)包含16个缺失值,用”?”标出。
pandas使用
pd.read_csv(’’,names=column_names)
- column_names:指定类别名字,['Sample code number','Clump Thickness', 'Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion','Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class']
- return:数据
- replace(to_replace=’’,value=):返回数据
- dropna():返回数据
分类流程
1、网上获取数据(工具pandas)
2、数据缺失值处理、标准化
3、LogisticRegression估计器流程
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report
def logistic():
"""
逻辑回归做二分类癌症预测
:return:
"""
### 构造列标签名字
column = ['Sample code number','Clump Thickness,Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion' ,
'Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli','Mitoses','Class']
### 读取数据
data = pd.read_csv("./案例/04 -肿瘤预测/breast-cancer-wisconsin.data",names=column)
### 缺失值处理
data = data.replace(to_replace='?',value=np.nan)
data = data.dropna() # 把nan删掉
x_train,x_test,y_train,y_test = train_test_split(data[column[0:9]],data[column[9]],test_size=0.25)
### 进行标准化
std = StandardScaler()
x_train = std.fit_transform(x_train)
x_test = std.fit_transform(x_test)
### 逻辑回归预测
lo = LogisticRegression()
lo.fit(x_train,y_train)
print(lo.coef_)
y_predict = lo.predict(x_test)
print("准确率:",lo.score(x_test,y_test))
print('召回率:',classification_report(y_test,y_predict,labels=[2, 4],target_names=['良性','恶性']))
return None
if __name__ == '__main__':
logistic()准确率: 0.9590643274853801
召回率: precision recall f1-score support
良性 0.98 0.96 0.97 116
恶性 0.91 0.96 0.94 55
accuracy 0.96 171
macro avg 0.95 0.96 0.95 171
weighted avg 0.96 0.96 0.96 171LogisticRegression回归案例——上下文点击
Avito Context Ad Clicks | Kaggle
LogisticRegression总结
应用:广告点击率预测、电商购物搭配推荐,是否患病,金融诈骗
优点:适合需要得到一个分类概率的场景,简单,速度快
缺点:当特征空间很大时,逻辑回归的性能不是很好(看硬件能力),不好处理多分类问题
多分类问题
决策树、随机森林、神经网络中的softmax方法——图像识别
朴素贝叶斯——文本分类
生成模型和判别模型
有没有先验概率(总结历史数据的先验信息)
无(判别模型)——K-近邻、决策树、随机森林、神经网络
有(生成模型)——朴素贝叶斯、隐马尔可夫模型
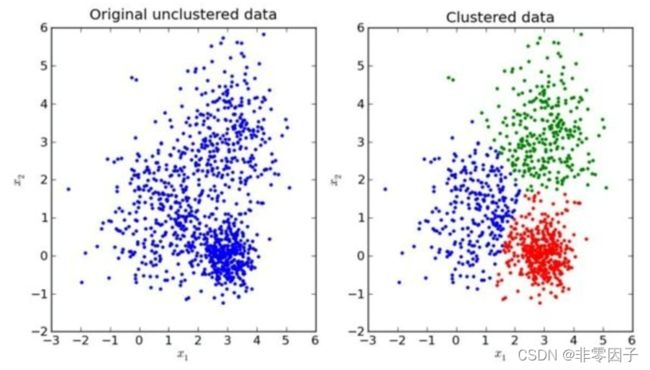
无监督学习——K-means
“物以类聚,人以群分”
k-means步骤
1、随机设置K个特征空间内的点作为初始的聚类中心
2、对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
3、接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值)
4、如果计算得出的新中心点与原中心点一样,那么结束,否则重新进行第二步过程
k-means API
sklearn.cluster.KMeans(n_clusters=8,init=‘k-means++’)
- k-means聚类
- n_clusters:开始的聚类中心数量
- init:初始化方法,默认为'k-means ++’
- labels_:默认标记的类型,可以和真实值比较(不是值比较)
Kmeans性能评估指标
轮廓系数:
注:对于每个点i 为已聚类数据中的样本 ,![]() 为i 到其它族群的所有样本的平均距离,
为i 到其它族群的所有样本的平均距离,![]() 为i 到本身簇的距离平均值
为i 到本身簇的距离平均值
最终计算出所有的样本点的轮廓系数平均值
如果![]() 小于0,说明
小于0,说明![]() 的平均距离大于最近的其他簇。聚类效果不好
的平均距离大于最近的其他簇。聚类效果不好
如果![]() 越大,说明
越大,说明![]() 的平均距离小于最近的其他簇。聚类效果好
的平均距离小于最近的其他簇。聚类效果好
轮廓系数的值是介于 [-1,1] ,越趋近于1代表内聚度和分离度都相对较优
API
sklearn.metrics.silhouette_score (X, labels)
- 计算所有样本的平均轮廓系数
- X:特征值
- labels:被聚类标记的目标值
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from matplotlib import pyplot as plt
from sklearn.metrics import silhouette_score
def cluster():
"""
聚类分析
:return:
"""
aisles = pd.read_csv('./案例/01-instacart/aisles.csv')
prior = pd.read_csv('./案例/01-instacart/order_products__prior.csv')
orders = pd.read_csv('./案例/01-instacart/orders.csv')
products = pd.read_csv('./案例/01-instacart/products.csv')
# print(aisles.head())
# print(prior.head())
# print(orders.head())
# print(products.head())
m_g = pd.merge(prior,orders,on=['order_id','order_id'])
m_g = pd.merge(m_g,products,on=['product_id','product_id'])
m_t = pd.merge(m_g,aisles,on=['aisle_id','aisle_id'])
# print(m_t.head())
cross = pd.crosstab(m_t['user_id'],m_t['aisle'])
# print(cross.head())
pca = PCA(n_components=0.9)
data = pca.fit_transform(cross)
x = data[:500]
# print(x.shape)
km = KMeans(n_clusters=4)
km.fit(x)
predict = km.predict(x)
# print(predict)
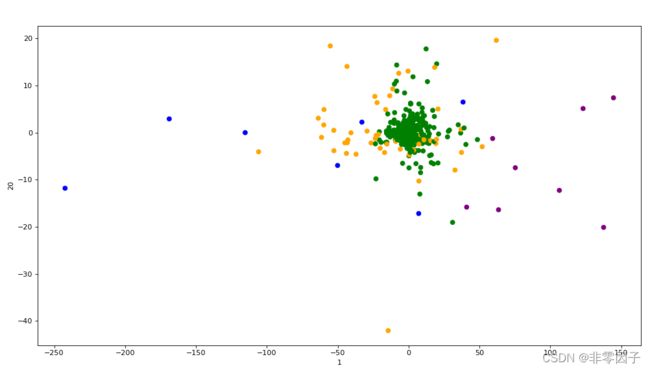
plt.figure(figsize=(15,8),dpi=80)
color_ = ['orange', 'green', 'blue', 'purple']
corl = [color_[i] for i in predict]
plt.scatter(x[:,1],x[:,20],color=corl)
plt.xlabel('1')
plt.ylabel('20')
# plt.show()
score = silhouette_score(x,predict)
print(score)
if __name__ == '__main__':
cluster()0.6394263094431663总结
特点分析:
采用迭代式算法,直观易懂并且非常实用
缺点:容易收敛到局部最优解(多次聚类)
需要预先设定簇的数量(k-means++解决)