算法：（八）树

8.1 二叉树的深度优先搜索

二叉树的遍历

// 递归中序遍历
public LinkedList inorderTraversalRecursion(TreeNode root){
    LinkedList<TreeNode> nodes = new LinkedList();
    dfsInOrder(root, nodes);
    return nodes;
}
public void dfsInOrder(TreeNode root, LinkedList nodes){
    if(root != null){
        dfsInOrder(root.leftChild, nodes);
        nodes.add(root);
        dfsInOrder(root.rightChild, nodes);
    }
}

// 非递归中序遍历
public LinkedList inorderTraversalNonRecursive(TreeNode root){
    LinkedList<TreeNode> nodes = new LinkedList<>();
    Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root;
    while(cur != null || !stack.isEmpty()){
        while(cur != null){
            stack.push(cur);
            cur = cur.leftChild;
        }
        cur = stack.pop();
        nodes.add(cur);
        cur = cur.rightChild;
    }
    return nodes;
}

// 递归前序遍历
public LinkedList<TreeNode> preorderTraversalRecursion(TreeNode root){
    LinkedList<TreeNode> nodes = new LinkedList<>();
    dfsPreorder(root, nodes);
    return nodes;
}

private void dfsPreorder(TreeNode root, LinkedList<TreeNode> nodes) {
    if(root != null){
        nodes.add(root);
        dfsPreorder(root.leftChild, nodes);
        dfsPreorder(root.rightChild, nodes);
    }
}

// 非递归中序遍历
public LinkedList<TreeNode> preorderTraversalNonRecursion(TreeNode root){
    LinkedList<TreeNode> nodes = new LinkedList<>();
    Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root;
    while(cur != null || !stack.isEmpty()){
        while(cur != null){
            nodes.add(cur);
            stack.push(cur);
            cur = cur.leftChild;
        }
        cur = stack.pop();
        cur = cur.rightChild;
    }
    return nodes;
}

// 递归后序遍历
public LinkedList<TreeNode> postorderTraversalRecursion(TreeNode root) {
    LinkedList<TreeNode> nodes = new LinkedList<>();
    dfsPostorder(root, nodes);
    return nodes;
}

private void dfsPostorder(TreeNode root, LinkedList<TreeNode> nodes) {
    if(root != null){
        dfsPostorder(root, nodes);
        dfsPostorder(root, nodes);
        nodes.add(root);
    }
}

// 非递归后序遍历
public LinkedList<TreeNode> postorderTraversalNonRecursion(TreeNode root){
    LinkedList<TreeNode> nodes = new LinkedList<>();
    Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root;
    // prev记录上次遍历的节点是不是当前节点的柚子节点。若是，则说明右子树已经遍历完毕，可以遍历当前节点；若不是，则要遍历右子树
    TreeNode prev = null;
    while(cur != null || !stack.isEmpty()){
        while(cur != null){
            stack.push(cur);
            cur = cur.leftChild;
        }
        cur = stack.peek();
        // 判断应该遍历右子树还是要遍历当前节点
        if(cur.rightChild != null && prev != cur.rightChild){
            cur = cur.rightChild;
        } else {
            stack.pop();
            nodes.add(cur);
            prev = cur;
            // 下一次遍历的一定是它的父亲节点，而父亲节点之前已经入栈，此时将cur置空，下一次弹出其父亲节点
            cur = null;
        }
    }
    return nodes;
}

面试题47：二叉树剪枝

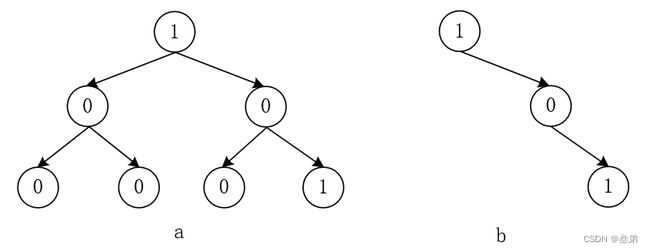
题目：一颗二叉树的所有节点要么是0，要么是1，请剪除二叉树中所有节点值全是0的子树。如下图，剪除a中左右节点为0的子树之后的结果如图b所示。

public TreeNode pruningTree(TreeNode root){
    // 如果一个节点可以被删除，则其左右子节点都可以被删除，所以操作当前节点之前必须操作左右子节点
	// 二叉树的后序遍历可以解决这个问题
    // 后序遍历二叉树，如果当前节点左右子树的节点值都为0，且自身的节点值也为0，则说明此节点可以删除
    if(root == null){
        return null;
    }
    root.leftChild = pruningTree(root.leftChild);
    root.rightChild = pruningTree(root.rightChild);
    if(root.leftChild == null && root.rightChild == null && root.value == 0){
        return null;
    }
    return root;
}

面试题48：序列化和反序列化二叉树

题目：请设计一个算法，将二叉树序列化成一个字符串，并能将字符串反序列化成原来的二叉树。

// 使用前序遍历进行序列化，同时使用前序遍历进行反序列化
// 在遍历到null节点时，用符号"#"保存null节点的信息
// 节点之间用","分隔
public String serialize(TreeNode root){
    if(root == null){
        return "#";
    }
    String leftStr = serialize(root.leftChild);
    String rightStr = serialize(root.rightChild);
    return root.value + "," + leftStr + "," + rightStr;
}
public TreeNode deserialize(String data){
    String[] nodeStr = data.split(",");
    int[] i = {0};
    return dfs(nodeStr, i);
}

private TreeNode dfs(String[] nodeStr, int[] i) {
    String str = nodeStr[i[0]];
    i[0]++;
    if(str == "#"){
        return null;
    }
    TreeNode node = new TreeNode(Integer.parseInt(str));
    node.leftChild = dfs(nodeStr, i);
    node.rightChild = dfs(nodeStr, i);
    return node;
}

面试题49：从根节点到叶节点的路径数字之和

题目：在一颗二叉树中所有节点都在0~9的范围之内，从根节点到叶节点的路径表示一个数字。求二叉树中所有路径表示的数字之和。如下图二叉树有三条从根节点到叶节点的路径，他们分别表示数字395、391和302，这三个数字之和为1088。

public int sumNumbers(TreeNode root){
    return dfs(root, 0);
}

private int dfs(TreeNode root, int path) {
    // 如果当前节点为null，则说明此子树没有路径，路径和为0
    if(root == null){
        return 0;
    }
    // 每加深一层，当前节点的路径基数*10，路径基数不代表此子树的路径和
    path = path + 10 + root.value;
    // 若左右子节点都为空，则说明到了叶子结点，赶回此节点路径基数
    if(root.leftChild == null && root.rightChild == null){
        return path;
    }
    // 否则返回左右子树路径和
    return dfs(root.leftChild, path) + dfs(root.rightChild, path);
}

面试题50：向下的路径节点值之和

题目：给定一颗二叉树和一个值sum，求二叉树中节点值之和等于sum的路径的数目。路径的定义为二叉树中顺着子节点的指针向下移动所经过的节点，但不一定从根节点开始，也不一定到叶节点结束。如下如二叉树中，有两条路径的节点值之和等于8。

public int pathSum(TreeNode root, int sum){
    // map记录一条路径上面所有的节点带根节点的路径和
    Map<Integer, Integer> map = new HashMap();
    map.put(0, 1);
    return dfs(root, sum, map, 0);
}

private int dfs(TreeNode root, int sum, Map<Integer, Integer> map, int path) {
    if(root == null){
        return 0;
    }
    // 当前节点的路径和
    path += root.value;
    // 看看此条路径上有没有节点的值为path - sum，有则说明此节点到当前节点的路径和为sum
    int count = map.getOrDefault(path - sum, 0);
    // map记录一条路径上面所有的节点带根节点的路径和
    map.put(path, map.getOrDefault(path, 0) + 1);
    // 递归子节点
    count += dfs(root.leftChild, sum, map, path);
    count += dfs(root.rightChild, sum, map, path);
    // 当前节点计算完毕，返回上层节点之前，从路径中删除当前节点
    map.put(path, map.get(path) - 1);

    return count;
}

面试题51：节点值之和最大的路径

public int maxPathSum(TreeNode root){
    int maxSum[] = {Integer.MIN_VALUE};
    dfs(root, maxSum);
    return maxSum[0];
}
private int dfs(TreeNode root, int[] maxSum) {
    if(root == null){
        return 0;
    }
    int[] maxSumLeft = {Integer.MIN_VALUE};
    int left = Math.max(0, dfs(root.leftChild, maxSumLeft));
    int[] maxSumRight = {Integer.MIN_VALUE};
    int right = Math.max(0, dfs(root.rightChild, maxSumRight));
    // 计算左右子节点路径最大值
    maxSum[0] = Math.max(maxSumLeft[0], maxSumRight[0]);
    // 若加上当前节点，计算出当前节点和左右节点组合的最大值
    // 保存的值是可以同时经过左右子树的路径
    maxSum[0] = Math.max(maxSum[0], root.value + left + right);
    // 返回值是不能同时经过左右子树的路径
    return root.value + Math.max(left, right);
}

8.2 二叉搜索树

• 二叉搜索树的左子节点总是小于当前节点，右子结点总是大于当前节点

二叉搜索树的查找

public TreeNode searchBST(TreeNode root, int val){
    TreeNode cur = root;
    while(cur != null){
        if(cur.value = val){
            break;
        }
        if(val < cur.val){
            cur = cur.leftChild;
        } else {
            cur = cur.rightChild;
        }
    }
    return cur;
}

面试题52：展平二叉搜索树

题目：给定一颗二搜索树，请调整节点的指针，使每个节点都没有左子节点。调整之后的树看起来像一个链表，但仍然是一棵二叉搜索树。

public TreeNode increasingBST(TreeNode root){
    // 二叉树中序遍历，遍历的同时进行指针的更改
    // 需要一个记录上一个操作节点的指针prev
    Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root;
    TreeNode prev = null;
    TreeNode first = null;
    while(cur != null || !stack.isEmpty()){
        while( cur!= null){
            stack.push(cur);
            cur = cur.leftChild;
        }
        cur = stack.pop();
        if(prev != null){
            prev.rightChild = cur;
        } else {
            first = cur;
        }
        prev = cur;
        cur.leftChild = null;
        cur = cur.rightChild;
    }
    return first;
}

面试题53：二叉搜索树的下一个节点

题目：给定一颗二叉搜索树和它的一个节点p，请找出按中序遍历的顺序该节点p的下一个节点。假设二叉搜索树中节点的值都是唯一的。

// 中序遍历的方式
public TreeNode nextNode(TreeNode root, TreeNode target){
    Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root;
    boolean isFound = false;
    while(cur != null || !stack.isEmpty()){
        while(cur != null){
            stack.push(cur);
            cur = cur.leftChild;
        }
        cur = stack.pop();
        if(isFound){
            break;
        } else if (cur == target){
            isFound = true;
        }
        cur = cur.rightChild;
    }
    return cur;
}
// 小Trick：使用查找的方式
// 思路是直接从根节点查找，如果当前节点的值小于等于目标节点，则说明目标节点的下一个节点在当前节点的右子树中；
// 如果当前节点大于目标节点，则说明当前节点可能是就是目标节点的下一个节点，或者目标节点的下一个节点在当前节点的左子树中；
// 所以先记录当前的节点，在遍历当前节点的左子树看看是否还有更小的大于目标值的节点
// 以此类推直到找到满足条件的最小节点
public TreeNode nextNodePro(TreeNode root, TreeNode target){
    TreeNode cur = root;
    TreeNode result = null;
    while(cur != null){
        if(cur.value <= target.value){
            cur = cur.rightChild;
        } else {
            result = cur;
            cur = cur.leftChild;
        }
    }
    return result;
}

面试题54：所有大于或等于节点的值之和

题目：给定一颗二叉搜索树，请假它的每个节点的值替换成树中大于或等于该节点值的所有节点之和。假设二叉搜索树的节点唯一。如下图所示，由于有两个节点的值大于或等于6，因此节点6替换成13，其他节点的替换过程与此类似。二叉搜索树中最大的节点不变。

// 从大到小中序遍历二叉树即可完成本题
public TreeNode reverseTraversal(TreeNode root){
    Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root;
    int sum = 0;
    while(cur != null || !stack.isEmpty()){
        while(cur != null){
            stack.push(cur);
            cur = cur.rightChild;
        }
        cur = stack.pop();
        sum =+ cur.value;
        cur.value = sum;
        cur = cur.leftChild;
    }
    return root;
}
// 另外的思路是两次遍历二叉树，第一次遍历可以用任意遍历方式得出二叉树的节点值总和sum，第二次遍历必须中序遍历，求得比当前节点值小的所有节点之和minSum
// 然后用sum - minSum即可得到大于等于当前节点的所有节点的和

面试题55：二叉搜索树迭代器

题目：请实现二叉搜索树的跌代理BSTIterator，它主要有如下是那个函数：

• 构造函数：输入二叉搜索树的根节点初始化该迭代器。
• 函数next：返回二叉搜索树中下一个最小的节点的值。
• 函数hasNext：返回二叉搜索树是否还有下一个节点。

// 中序遍历可以得到一个二叉搜索树的排序
// 若允许修改二叉树的结构，则将其二叉树展平即可
// 若不予许修改二叉树的结构，则将二叉树转化成一个顺序链表即可

// 小trick：熟悉非递归中序遍历算法可知，外层while循环的判断条件就是判断是否遍历到树的最后一个节点，而循环体
public class BSTIterator {
    TreeNode cur;
    Stack<TreeNode> stack;
    public BSTIterator(TreeNode root){
        this.cur = root;
        stack = new Stack<>();
    }
    public boolean hasNext(){
        return cur != null || !stack.isEmpty();
    }
    
    public int next(){
        while(cur != null){
            stack.push(cur);
            cur = cur.leftChild;
        }
        cur = stack.pop();
        int val = cur.value;
        cur = cur.rightChild;
        return val;
    }
}

面试题56：二叉搜索树中两个节点的值之和

题目：给定一颗二叉搜索树和一个值k，请判断该二叉搜索树中是否存在值之和等于k的两个节点。假设二叉搜索树中节点的均值唯一。

// Hash表法
public boolean findTarget(TreeNode root, int k){
    Set<Integer> set = new HashSet<>();
    Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root;
    while (cur != null || !stack.isEmpty()) {
        while (cur != null) {
            stack.push(cur);
            cur = cur.leftChild;
        }
        cur = stack.pop();
        if (set.contains(k - cur.value)) {
            return true;
        } else {
            set.add(cur.value);
        }
        cur = cur.rightChild;
    }
    return false;
}

// 双指针法：头尾指针，需要两次遍历：从小到大遍历，从大到小遍历。
// 从小到大遍历：见面试题55
// 从大到小遍历：
public boolean findTargetPro(TreeNode root, int k){
        if(root == null){
            return false;
        }
        BSTIterator head = new BSTIterator(root);
        BSTIteratorReverse tail = new BSTIteratorReverse(root);
        int next = head.next();
        int prev = tail.prev();
        while(next != prev){
            if (next + prev == k){
                return true;
            }
            if(next + prev < k){
                next = head.next();
            } else if(next + prev > k){
                prev = tail.prev();
            }
        }
        return false;
    }
}


class BSTIteratorReverse{
    TreeNode cur;
    Stack<TreeNode> stack;

    public BSTIteratorReverse(TreeNode root) {
        this.cur = root;
        stack = new Stack<>();
    }

    public boolean hasNext(){
        return cur != null || !stack.isEmpty();
    }

    public int prev(){
        while(cur != null){
            stack.push(cur);
            cur = cur.rightChild;
        }
        cur = stack.pop();
        int val = cur.value;
        cur = cur.leftChild;
        return val;
    }
}

8.4 TreeSet和TreeMap的应用

面试题57：值和下标之差都在给定范围内

题目：给定一个整数数组nums和两个整数k，t，请判断是否存在两个不同的下标i和j满足i和j只差的绝对值不大于给定的k，并且两个数值nums[i]和nums[j]的差的绝对值不大于给定的t。

public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t){
    // k表示数据间隔
    // t表示差值
    TreeSet<Integer> set = new TreeSet<>();
    for(int i = 0; i < nums.length; i++){
        Integer floor = set.floor(nums[i]);
        if(floor != null && floor >= nums[i] - t){
            return true;
        }
        Integer ceiling = set.ceiling(nums[i]);
        if (ceiling != null && ceiling <= nums[i] + t) {
            return true;
        }
        set.add(nums[i]);
        if(i > k){
            set.remove(nums[i - k]);
        }
    }
    return false;
}
// 小trick：使用桶来进行查找
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t){
    Map<Integer, Integer> map = new HashMap<>();
    int bucketSize = t + 1;
    for(int i = 0; i < nums.length; i++){
        int id = getBucketId(nums[i], bucketSize);
        if(map.containsKey(id) ||
           (map.containsKey(id - 1) && map.get(id - 1) >= nums[i] - t )||
           (map.containsKey(id + 1) || map.get(id + 1) <= nums[i] + t)){
            return true;
        }
        map.put(bucketSize, nums[i]);
        if(i > k){
            map.remove(getBucketId(nums[i - k], bucketSize));
        }
    }
    return false;
}

private int getBucketId(int num, int bucketSize) {
    return num > 0 ? num / bucketSize : (num + 1) / bucketSize - 1 ;
}

面试题58：日程表

题目：请实现一个类型MyCalendar用来记录自己的日程安排，该类型用方法book(int start, int end)在日程表中添加一个时间区域为[start, end)的事项。如果[start, end)中没有安排其他事项，则成功添加该事项，并返回true；否则，不能添加该事项，返回false。例如，下面三次调用book方法中，第二次条用返回false，这是因为[15, 20)已经被第一次调用占据了。第一次条用是一个半开区间[10, 20)，不影响第三次调用的区间[20, 30)：

MyCalendar cal = new MyCalendar();

cal.book(10, 20);

cal.book(15, 25);

cal.book(20, 30);

// 使用TreeMap保存事项的时间区间。
// 每次插入的时候从TreeMap中找到开始时间小于start的最晚的一个事项，然后在找开始时间大于start的最早的一个事项，确保这两个事项一定是相邻的
// 然后判断在两个事项之间是否可以插入当前事项
TreeMap<Integer, Integer> map;

public MyCalendar_58() {
    this.map = new TreeMap<>();
}

public boolean book(int start, int end) {
    Integer ceilingKey = map.ceilingKey(start);
    Integer floorKey = map.floorKey(start);
    if (ceilingKey != null && start < map.get(ceilingKey)){
        return false;
    }
    if (floorKey != null && end > floorKey) {
        return false;
    }
    map.put(start, end);
    return true;
}