2022-4-18至2022-4-24周报

摘要

There are three portions in the artical. In the first part, I read the thesis named Time-series Generative Adversarial Networks, and I reappeared this framework in the second part. At the end of the artical, I recorded some knowledge points of the optimizer of deep learning.

论文阅读

Time-series Generative Adversarial Networks

• 会议：NeurIPS 2019
• 作者及单位：Jinsung Yoon，Daniel Jarrett，Mihaela van der Schaar；加利福尼亚大学，剑桥大学，艾伦图灵研究所

论文摘要

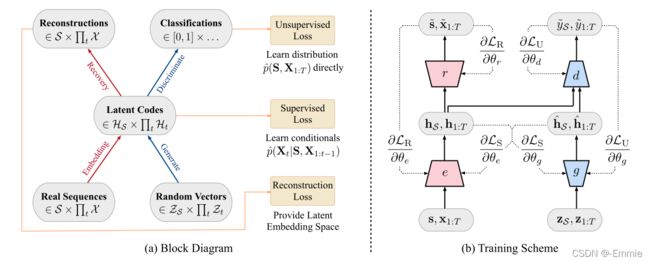
提出了一个时间序列数据生成模型TimeGAN，能够生成真实的temporal dynamics.
该框架将无监督GAN方法的多功能性与有监督的自回归模型提供的条件概率原理结合，来生成保留时间动态的时间序列。
并且定性和定量地评估该方法使用各种真实和合成数据集生成真实样本的能力，均可以始终显著优于最先进的基准。

研究内容

TimeGAN：

1.除了利用无监督学习的real和fake样本的对抗loss，还引入了，用原始数据作为监督项的逐步监督损失，明确的让模型捕捉序列数据中的逐步条件分布。这样做的好处是，比起到达基准是真实的还是合成的，训练数据中的信息更多。 我们可以从真实序列的转移动态中明确学习。
2.引入了一种嵌入网络embedding network，以提供特征和潜在表示之间的可逆映射，从而降低了对抗性学习空间的高维性。这利用了以下事实：即使是复杂系统的时间动态也往往是由较少且较低维的变化因素驱动的。
3.重要的是，通过联合训练嵌入网络和生成器网络，可以将监督损失最小化，以使潜在空间不仅可以提高参数效率，而且还可以通过特定条件来方便生成器学习时间关系。
4.最后，将框架通用化以处理混合数据设置，在该设置中可以同时生成静态数据和时间序列数据。

创新点

1.无监督GAN与有监督的自回归的第一次结合。
2.定性地，进行t-SNE 和PCA分析以可视化生成的分布与原始分布的相似程度。
3.定量的，事后分类器如何区分真实序列和生成序列。 此外，通过将“综合训练，真实测试（TSTR）”框架应用于序列预测任务，可以评估生成的数据保留原始数据的预测特征的程度。

作者的研究思路或研究方法

一个好的时间序列数据生成模型应该保持时间动态，即新序列尊重跨时间变量之间的原始关系。将生成性对抗网络（GAN）引入序列环境的现有方法没有充分考虑时间序列数据特有的时间相关性。同时，允许对网络动态进行更精细控制的序列预测监督模型具有固有的确定性。总之，时序生成模型不仅应该捕捉每个时间步的特征分布，还需要捕捉时间步之间潜在的复杂的关系。

一些相关的工作：
一方面，自回归模型明确的将时间序列模型，分解为条件分布的乘积。尽管自回归方法在预测中很有效，但是本质上是确定性的。从无需添加外部条件就能获得新序列的角度看，也不是一种“生成”方法。
另一方面，直接用RNN初始化GAN生成，这种直接简单地对于序列数据应用标准的loss函数，不能满足捕捉序列之间的逐步依赖关系。

因此作者将两者结合起来提出新的机制可以显式的保留temporal dynamics。

用哪些数据来论证的

数据集：

• Stock（真实数据集1）：多变量时间序列，特征之间有相关， 连续实值，具有周期性。volume and high, low, opening, closing, and adjusted closing prices等特征
• Sine（合成数据集）：模拟具有不同频率η和相位θ的多元正弦序列，提供连续值，周期性，多元数据，其中每个特征彼此独立
• Energy（真实数据集2）：具有高噪声周期性，较高维数和相关特征的数据集。 UCI Appliances的能量预测数据集由多变量，连续值的测量组成，包括以紧密间隔测量的众多时间特征
• Event（离散数据集）：离散值和不规则时间戳为特征的数据集。 我们使用由事件序列及其时间组成的大型私人肺癌通路数据集，并对事件类型的单编码序列以及事件时间进行建模

评测指标：多样性、保真度、实用性（用合成的样本训练，测试真实样本）
可视化：t-SNE和PCA在二维平面进行模型分布比较。
判别得分（discrimination score）：真是样本标为1，合成样本标为0；训练一个现成的LSTM分类器，然后用测试集的错误率作为得分。
预测得分（predictive score）：用合成样本集训练一个LSTM模型，预测下一时间步的值。再用模型在原始数据集测试。

对比方法：
类似的方法：RCGAN，C-RNN-GAN
自回归模型：RNN with Teacher-forcing/Professor-forcing
额外的：WaveGAN（基于WaveNet）

论文复现

数据处理

对于真实数据集1股票数据集：

1. 原始数据下载
   每天更新的股票交易数据，可以看到原始数据存在一些缺失
   
   笔者选择了近五年的交易记录，下载重命名为stock_data.csv文件
   
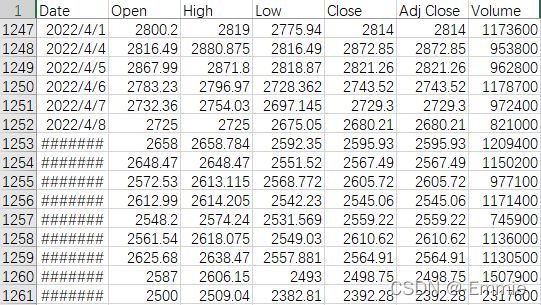
   注意这里的Date列需要将日期处理，否则会报could not convert string to float数值错误
   
   

2. 处理数据
   将Date列删除掉，其他数据不变。这样数据集依然是时序数据。

3. 处理后的结果
   股票数据集含有6个变量：Open, High, Low, Close, Adj Close, Volume且含有1260项近五年的记录
   

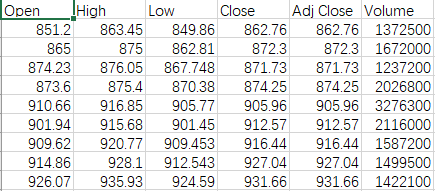
源码理解

将原始时间序列数据转换为预处理的时间序列数据，且生成正弦数据集：data_loading.py

import numpy as np

def MinMaxScaler(data):

  numerator = data - np.min(data, 0)
  denominator = np.max(data, 0) - np.min(data, 0)
  norm_data = numerator / (denominator + 1e-7)
  return norm_data


def sine_data_generation (no, seq_len, dim):

  # Initialize the output
  data = list()

  # Generate sine data
  for i in range(no):      
    # Initialize each time-series
    temp = list()
    # For each feature
    for k in range(dim):
      # Randomly drawn frequency and phase
      freq = np.random.uniform(0, 0.1)            
      phase = np.random.uniform(0, 0.1)
          
      # Generate sine signal based on the drawn frequency and phase
      temp_data = [np.sin(freq * j + phase) for j in range(seq_len)] 
      temp.append(temp_data)
        
    # Align row/column
    temp = np.transpose(np.asarray(temp))        
    # Normalize to [0,1]
    temp = (temp + 1)*0.5
    # Stack the generated data
    data.append(temp)
                
  return data
    

def real_data_loading (data_name, seq_len):

  assert data_name in ['stock','energy']
  
  if data_name == 'stock':
    ori_data = np.loadtxt('data/stock_data.csv', delimiter = ",",skiprows = 1)
  elif data_name == 'energy':
    ori_data = np.loadtxt('data/energy_data.csv', delimiter = ",",skiprows = 1)
        
  # Flip the data to make chronological data
  ori_data = ori_data[::-1]
  # Normalize the data
  ori_data = MinMaxScaler(ori_data)
    
  # Preprocess the dataset
  temp_data = []    
  # Cut data by sequence length
  for i in range(0, len(ori_data) - seq_len):
    _x = ori_data[i:i + seq_len]
    temp_data.append(_x)
        
  # Mix the datasets (to make it similar to i.i.d)
  idx = np.random.permutation(len(temp_data))    
  data = []
  for i in range(len(temp_data)):
    data.append(temp_data[idx[i]])
    
  return data

使用原始时间序列数据作为训练集生成合成时序数据：timegan.py

import tensorflow as tf
import numpy as np
from utils import extract_time, rnn_cell, random_generator, batch_generator


def timegan (ori_data, parameters):
  """TimeGAN function.
  
  Use original data as training set to generater synthetic data (time-series)
  
  Args:
    - ori_data: original time-series data
    - parameters: TimeGAN network parameters
    
  Returns:
    - generated_data: generated time-series data
  """
  # Initialization on the Graph
  tf.reset_default_graph()

  # Basic Parameters
  no, seq_len, dim = np.asarray(ori_data).shape
    
  # Maximum sequence length and each sequence length
  ori_time, max_seq_len = extract_time(ori_data)
  
  def MinMaxScaler(data):
    """Min-Max Normalizer.
    
    Args:
      - data: raw data
      
    Returns:
      - norm_data: normalized data
      - min_val: minimum values (for renormalization)
      - max_val: maximum values (for renormalization)
    """    
    min_val = np.min(np.min(data, axis = 0), axis = 0)
    data = data - min_val
      
    max_val = np.max(np.max(data, axis = 0), axis = 0)
    norm_data = data / (max_val + 1e-7)
      
    return norm_data, min_val, max_val
  
  # Normalization
  ori_data, min_val, max_val = MinMaxScaler(ori_data)
              
  ## Build a RNN networks          
  
  # Network Parameters
  hidden_dim   = parameters['hidden_dim'] 
  num_layers   = parameters['num_layer']
  iterations   = parameters['iterations']
  batch_size   = parameters['batch_size']
  module_name  = parameters['module'] 
  z_dim        = dim
  gamma        = 1
    
  # Input place holders
  X = tf.placeholder(tf.float32, [None, max_seq_len, dim], name = "myinput_x")
  Z = tf.placeholder(tf.float32, [None, max_seq_len, z_dim], name = "myinput_z")
  T = tf.placeholder(tf.int32, [None], name = "myinput_t")
  
  def embedder (X, T):
    """Embedding network between original feature space to latent space.
    
    Args:
      - X: input time-series features
      - T: input time information
      
    Returns:
      - H: embeddings
    """
    with tf.variable_scope("embedder", reuse = tf.AUTO_REUSE):
      e_cell = tf.nn.rnn_cell.MultiRNNCell([rnn_cell(module_name, hidden_dim) for _ in range(num_layers)])
      e_outputs, e_last_states = tf.nn.dynamic_rnn(e_cell, X, dtype=tf.float32, sequence_length = T)
      H = tf.contrib.layers.fully_connected(e_outputs, hidden_dim, activation_fn=tf.nn.sigmoid)     
    return H
      
  def recovery (H, T):   
    """Recovery network from latent space to original space.
    
    Args:
      - H: latent representation
      - T: input time information
      
    Returns:
      - X_tilde: recovered data
    """     
    with tf.variable_scope("recovery", reuse = tf.AUTO_REUSE):       
      r_cell = tf.nn.rnn_cell.MultiRNNCell([rnn_cell(module_name, hidden_dim) for _ in range(num_layers)])
      r_outputs, r_last_states = tf.nn.dynamic_rnn(r_cell, H, dtype=tf.float32, sequence_length = T)
      X_tilde = tf.contrib.layers.fully_connected(r_outputs, dim, activation_fn=tf.nn.sigmoid) 
    return X_tilde
    
  def generator (Z, T):  
    """Generator function: Generate time-series data in latent space.
    
    Args:
      - Z: random variables
      - T: input time information
      
    Returns:
      - E: generated embedding
    """        
    with tf.variable_scope("generator", reuse = tf.AUTO_REUSE):
      e_cell = tf.nn.rnn_cell.MultiRNNCell([rnn_cell(module_name, hidden_dim) for _ in range(num_layers)])
      e_outputs, e_last_states = tf.nn.dynamic_rnn(e_cell, Z, dtype=tf.float32, sequence_length = T)
      E = tf.contrib.layers.fully_connected(e_outputs, hidden_dim, activation_fn=tf.nn.sigmoid)     
    return E
      
  def supervisor (H, T): 
    """Generate next sequence using the previous sequence.
    
    Args:
      - H: latent representation
      - T: input time information
      
    Returns:
      - S: generated sequence based on the latent representations generated by the generator
    """          
    with tf.variable_scope("supervisor", reuse = tf.AUTO_REUSE):
      e_cell = tf.nn.rnn_cell.MultiRNNCell([rnn_cell(module_name, hidden_dim) for _ in range(num_layers-1)])
      e_outputs, e_last_states = tf.nn.dynamic_rnn(e_cell, H, dtype=tf.float32, sequence_length = T)
      S = tf.contrib.layers.fully_connected(e_outputs, hidden_dim, activation_fn=tf.nn.sigmoid)     
    return S
          
  def discriminator (H, T):
    """Discriminate the original and synthetic time-series data.
    
    Args:
      - H: latent representation
      - T: input time information
      
    Returns:
      - Y_hat: classification results between original and synthetic time-series
    """        
    with tf.variable_scope("discriminator", reuse = tf.AUTO_REUSE):
      d_cell = tf.nn.rnn_cell.MultiRNNCell([rnn_cell(module_name, hidden_dim) for _ in range(num_layers)])
      d_outputs, d_last_states = tf.nn.dynamic_rnn(d_cell, H, dtype=tf.float32, sequence_length = T)
      Y_hat = tf.contrib.layers.fully_connected(d_outputs, 1, activation_fn=None) 
    return Y_hat   
    
  # Embedder & Recovery
  H = embedder(X, T)
  X_tilde = recovery(H, T)
    
  # Generator
  E_hat = generator(Z, T)
  H_hat = supervisor(E_hat, T)
  H_hat_supervise = supervisor(H, T)
    
  # Synthetic data
  X_hat = recovery(H_hat, T)
    
  # Discriminator
  Y_fake = discriminator(H_hat, T)
  Y_real = discriminator(H, T)     
  Y_fake_e = discriminator(E_hat, T)
    
  # Variables        
  e_vars = [v for v in tf.trainable_variables() if v.name.startswith('embedder')]
  r_vars = [v for v in tf.trainable_variables() if v.name.startswith('recovery')]
  g_vars = [v for v in tf.trainable_variables() if v.name.startswith('generator')]
  s_vars = [v for v in tf.trainable_variables() if v.name.startswith('supervisor')]
  d_vars = [v for v in tf.trainable_variables() if v.name.startswith('discriminator')]
    
  # Discriminator loss
  D_loss_real = tf.losses.sigmoid_cross_entropy(tf.ones_like(Y_real), Y_real)
  D_loss_fake = tf.losses.sigmoid_cross_entropy(tf.zeros_like(Y_fake), Y_fake)
  D_loss_fake_e = tf.losses.sigmoid_cross_entropy(tf.zeros_like(Y_fake_e), Y_fake_e)
  D_loss = D_loss_real + D_loss_fake + gamma * D_loss_fake_e
            
  # Generator loss
  # 1. Adversarial loss
  G_loss_U = tf.losses.sigmoid_cross_entropy(tf.ones_like(Y_fake), Y_fake)
  G_loss_U_e = tf.losses.sigmoid_cross_entropy(tf.ones_like(Y_fake_e), Y_fake_e)
    
  # 2. Supervised loss
  G_loss_S = tf.losses.mean_squared_error(H[:,1:,:], H_hat_supervise[:,:-1,:])
    
  # 3. Two Momments
  G_loss_V1 = tf.reduce_mean(tf.abs(tf.sqrt(tf.nn.moments(X_hat,[0])[1] + 1e-6) - tf.sqrt(tf.nn.moments(X,[0])[1] + 1e-6)))
  G_loss_V2 = tf.reduce_mean(tf.abs((tf.nn.moments(X_hat,[0])[0]) - (tf.nn.moments(X,[0])[0])))
    
  G_loss_V = G_loss_V1 + G_loss_V2
    
  # 4. Summation
  G_loss = G_loss_U + gamma * G_loss_U_e + 100 * tf.sqrt(G_loss_S) + 100*G_loss_V 
            
  # Embedder network loss
  E_loss_T0 = tf.losses.mean_squared_error(X, X_tilde)
  E_loss0 = 10*tf.sqrt(E_loss_T0)
  E_loss = E_loss0  + 0.1*G_loss_S
    
  # optimizer
  E0_solver = tf.train.AdamOptimizer().minimize(E_loss0, var_list = e_vars + r_vars)
  E_solver = tf.train.AdamOptimizer().minimize(E_loss, var_list = e_vars + r_vars)
  D_solver = tf.train.AdamOptimizer().minimize(D_loss, var_list = d_vars)
  G_solver = tf.train.AdamOptimizer().minimize(G_loss, var_list = g_vars + s_vars)      
  GS_solver = tf.train.AdamOptimizer().minimize(G_loss_S, var_list = g_vars + s_vars)   
        
  ## TimeGAN training   
  sess = tf.Session()
  sess.run(tf.global_variables_initializer())
    
  # 1. Embedding network training
  print('Start Embedding Network Training')
    
  for itt in range(iterations):
    # Set mini-batch
    X_mb, T_mb = batch_generator(ori_data, ori_time, batch_size)           
    # Train embedder        
    _, step_e_loss = sess.run([E0_solver, E_loss_T0], feed_dict={X: X_mb, T: T_mb})        
    # Checkpoint
    if itt % 1000 == 0:
      print('step: '+ str(itt) + '/' + str(iterations) + ', e_loss: ' + str(np.round(np.sqrt(step_e_loss),4)) ) 
      
  print('Finish Embedding Network Training')
    
  # 2. Training only with supervised loss
  print('Start Training with Supervised Loss Only')
    
  for itt in range(iterations):
    # Set mini-batch
    X_mb, T_mb = batch_generator(ori_data, ori_time, batch_size)    
    # Random vector generation   
    Z_mb = random_generator(batch_size, z_dim, T_mb, max_seq_len)
    # Train generator       
    _, step_g_loss_s = sess.run([GS_solver, G_loss_S], feed_dict={Z: Z_mb, X: X_mb, T: T_mb})       
    # Checkpoint
    if itt % 1000 == 0:
      print('step: '+ str(itt)  + '/' + str(iterations) +', s_loss: ' + str(np.round(np.sqrt(step_g_loss_s),4)) )
      
  print('Finish Training with Supervised Loss Only')
    
  # 3. Joint Training
  print('Start Joint Training')
  
  for itt in range(iterations):
    # Generator training (twice more than discriminator training)
    for kk in range(2):
      # Set mini-batch
      X_mb, T_mb = batch_generator(ori_data, ori_time, batch_size)               
      # Random vector generation
      Z_mb = random_generator(batch_size, z_dim, T_mb, max_seq_len)
      # Train generator
      _, step_g_loss_u, step_g_loss_s, step_g_loss_v = sess.run([G_solver, G_loss_U, G_loss_S, G_loss_V], feed_dict={Z: Z_mb, X: X_mb, T: T_mb})
       # Train embedder        
      _, step_e_loss_t0 = sess.run([E_solver, E_loss_T0], feed_dict={Z: Z_mb, X: X_mb, T: T_mb})   
           
    # Discriminator training        
    # Set mini-batch
    X_mb, T_mb = batch_generator(ori_data, ori_time, batch_size)           
    # Random vector generation
    Z_mb = random_generator(batch_size, z_dim, T_mb, max_seq_len)
    # Check discriminator loss before updating
    check_d_loss = sess.run(D_loss, feed_dict={X: X_mb, T: T_mb, Z: Z_mb})
    # Train discriminator (only when the discriminator does not work well)
    if (check_d_loss > 0.15):        
      _, step_d_loss = sess.run([D_solver, D_loss], feed_dict={X: X_mb, T: T_mb, Z: Z_mb})
        
    # Print multiple checkpoints
    if itt % 1000 == 0:
      print('step: '+ str(itt) + '/' + str(iterations) + 
            ', d_loss: ' + str(np.round(step_d_loss,4)) + 
            ', g_loss_u: ' + str(np.round(step_g_loss_u,4)) + 
            ', g_loss_s: ' + str(np.round(np.sqrt(step_g_loss_s),4)) + 
            ', g_loss_v: ' + str(np.round(step_g_loss_v,4)) + 
            ', e_loss_t0: ' + str(np.round(np.sqrt(step_e_loss_t0),4))  )
  print('Finish Joint Training')
    
  ## Synthetic data generation
  Z_mb = random_generator(no, z_dim, ori_time, max_seq_len)
  generated_data_curr = sess.run(X_hat, feed_dict={Z: Z_mb, X: ori_data, T: ori_time})    
    
  generated_data = list()
    
  for i in range(no):
    temp = generated_data_curr[i,:ori_time[i],:]
    generated_data.append(temp)
        
  # Renormalization
  generated_data = generated_data * max_val
  generated_data = generated_data + min_val
    
  return generated_data

以上源码有一处问题，在引入tensorflow时，发生了因为安装的Tensorflow 2不支持Tensorflow1的API而报的错

需要修改引入import tensorflow as tf 改为

import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()

报告数据集的判别和预测分数，以及t-SNE和PCA分析：main_timegan.py
指标和timeGAN的一些实用函数：utils.py（需要改tf引入）
原始数据和合成数据之间的PCA和t-SNE分析：discriminative.py（需要改tf引入）
使用Post-hoc RNN对原始数据和合成数据进行分类：predictive.py（需要改tf引入）

训练模型

加载数据并设定参数

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function

import numpy as np
import warnings
warnings.filterwarnings("ignore")

# 1. TimeGAN model
from timegan import timegan
# 2. Data loading
from data_loading import real_data_loading, sine_data_generation
# 3. Metrics
from metrics.discriminative_metrics import discriminative_score_metrics
from metrics.predictive_metrics import predictive_score_metrics
from metrics.visualization_metrics import visualization
data_name = 'stock'
seq_len = 24

if data_name in ['stock', 'energy']:
  ori_data = real_data_loading(data_name, seq_len)
elif data_name == 'sine':
  # Set number of samples and its dimensions
  no, dim = 10000, 5
  ori_data = sine_data_generation(no, seq_len, dim)
  
parameters = dict()

parameters['module'] = 'gru' 
parameters['hidden_dim'] = 24
parameters['num_layer'] = 3
parameters['iterations'] = 10000
parameters['batch_size'] = 128

运行TimeGAN来合成时序数据：

generated_data = timegan(ori_data, parameters)   

得到训练结果：

评估数据：

1. discriminative score: 0.173

metric_iteration = 5

discriminative_score = list()
for _ in range(metric_iteration):
    temp_disc = discriminative_score_metrics(ori_data, generated_data)
    discriminative_score.append(temp_disc)

2. predictive score: 0.081

predictive_score = list()
for tt in range(metric_iteration):
  temp_pred = predictive_score_metrics(ori_data, generated_data)
  predictive_score.append(temp_pred)

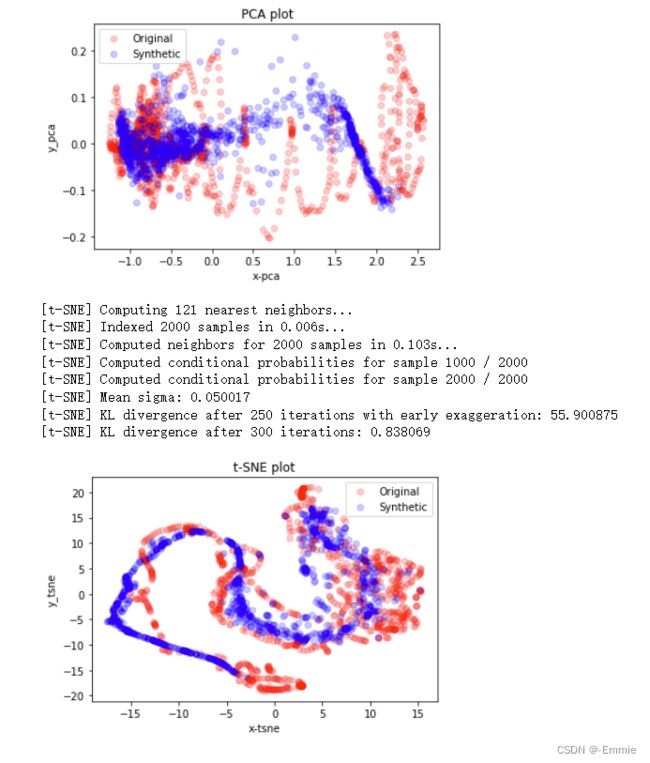
3. visualization

visualization(ori_data, generated_data, 'pca')
visualization(ori_data, generated_data, 'tsne')

基础知识

优化技巧

梯度消失和梯度爆炸

在数值稳定性方面，不稳定梯度影响数值表示，也威胁到我们优化算法的稳定性。
梯度消失问题是由每层的线性运算之后的激活函数导致的。当输入很大或很小时，sigmoid函数的梯度都会消失，如图。

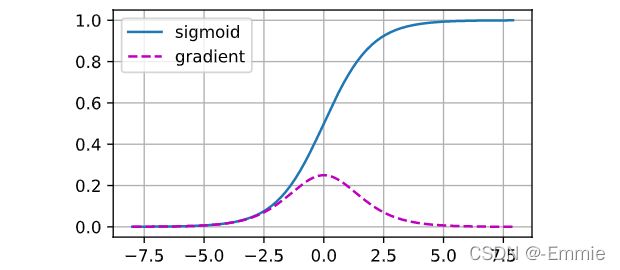
当反向传播很多层时，除非在刚刚好的地方，这些地方的输入接近于0，否则整个乘积的梯度会消失。

形成原因的数学表示：
一个L层、输入x、输出o的深层网络
每一层l由变换$f_l$定义，该变换的参数为权重$w^{(l)}$，其隐藏变量是$h^{(l)}$(令$h^{(0)}=x$)
我们的网络表示成$h^{(l)}=f_l(h^{(l-1)})$因此$o=f_L...f_1(x)$
如果所有隐藏变量和输入都是向量，我们可以将o关于任何一组参数$w^{(l)}$的梯度写成：

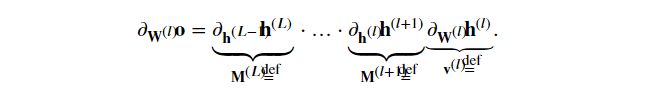
该梯度是L-l个矩阵$M^{(L)}...M^{(l+1)}$与梯度向量$v^{(l)}$的乘积
因此，我们容易受到数值下溢问题的影响，尤其当太多的概率乘在一起
处理概率的常见技巧是切换到对数空间，不幸的是数值下溢更严重：最初，矩阵$M^{(l)}$可能具有各种各样的特征值，它们可能很小，可能很大，它们的乘积可能非常小，也可能非常大。
梯度爆炸（gradient exploding）参数更新过大，破坏了模型的稳定收敛
梯度消失（gradient vanishing）参数更新过小，在每次更新时几乎不会移动，导致无法学习

dropout

一个好的预测模型应该在没看过的数据上有很好的表现。经典泛化理论认为，为了缩小训练和测试性能的差距，模型应该具有一定的简单性。参数的范数代表了一种有用的简单性度量，如权重衰减（L2正则化）。简单性的另一个有用角度是平滑性，即函数不应该对其输入的微小变化敏感。有前人证明，函数光滑和要求它对输入中的扰动具有适应性之间有明确的数学关系。一个聪明的实现是在训练过程中，在计算后续层之前向网络的每一层注入噪声。当训练一个有多层的深层网络时，注入噪声只会在输入-输出映射上增强平滑性。dropout在正向传播过程中，计算每一内部层的同时注入噪声。在整个训练过程的每一次迭代中，dropout包括在计算下一层之前将当前层中的一些节点置零。
那么如何注入噪声？