【李宏毅机器学习笔记】4、Classification

 

【李宏毅机器学习笔记】1、回归问题（Regression）

【李宏毅机器学习笔记】2、error产生自哪里？

【李宏毅机器学习笔记】3、gradient descent

【李宏毅机器学习笔记】4、Classification

【李宏毅机器学习笔记】5、Logistic Regression

【李宏毅机器学习笔记】6、简短介绍Deep Learning

【李宏毅机器学习笔记】7、反向传播（Backpropagation）

【李宏毅机器学习笔记】8、Tips for Training DNN

【李宏毅机器学习笔记】9、Convolutional Neural Network（CNN）

【李宏毅机器学习笔记】10、Why deep？（待填坑）

【李宏毅机器学习笔记】11、 Semi-supervised

【李宏毅机器学习笔记】 12、Unsupervised Learning - Linear Methods

【李宏毅机器学习笔记】 13、Unsupervised Learning - Word Embedding（待填坑）

【李宏毅机器学习笔记】 14、Unsupervised Learning - Neighbor Embedding（待填坑）

【李宏毅机器学习笔记】 15、Unsupervised Learning - Auto-encoder（待填坑）

【李宏毅机器学习笔记】 16、Unsupervised Learning - Deep Generative Model（待填坑）

【李宏毅机器学习笔记】 17、迁移学习（Transfer Learning）

【李宏毅机器学习笔记】 18、支持向量机（Support Vector Machine，SVM）

【李宏毅机器学习笔记】 19、Structured Learning - Introduction（待填坑）

【李宏毅机器学习笔记】 20、Structured Learning - Linear Model（待填坑）

【李宏毅机器学习笔记】 21、Structured Learning - Structured SVM（待填坑）

【李宏毅机器学习笔记】 22、Structured Learning - Sequence Labeling（待填坑）

【李宏毅机器学习笔记】 23、循环神经网络（Recurrent Neural Network，RNN）

【李宏毅机器学习笔记】 24、集成学习（Ensemble）

------------------------------------------------------------------------------------------------------

【李宏毅深度强化学习】视频地址：https://www.bilibili.com/video/av10590361?p=6

课件地址：http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML17_2.html

-------------------------------------------------------------------------------------------------------

用regression来解classification可行吗？

 以回归问题的做法来做分类问题，就是，在training data中，class 1有一个目标值为1，class 2 有一个目标值为-1。以这些数据去训练，希望在testing 阶段，能做到输入class 1 就输出接近1的值，输入class 2 就输出接近 -1 的值。

但是，实际上这是不可行的。

缺点1：

将刚才的例子画成图，理想情况就如左图那样，绿色就是分界线。

但是，也有例外，如右图，有一小部分class 1 的样本在比较远的地方（右下角）。虽然我们人眼能直接画出绿线这条分界线，但是机器不会，它直接按回归的方式去解最终会解出紫色这条分界线。因为机器考虑了右下角的点，所以使得原来的绿线发生偏移。

缺点2：

假设现在是多分类问题，class 1 目标值是1，class 2目标值是2，class 3 目标值是 3 。由于数字1和数字2接近，数字1和数字3比较远，就会间接造成class 1和class 2相像，而class 1和class 3 比较不像的误差。

Generative Model

 现在给出一只神奇宝贝 x ，想要通过的公式算出 x 属于神奇宝贝的哪一类别的话，需要知道

 （抽一个x，属于C1的概率）

  （在C1中抽到x的概率）

  （抽一个x，属于C2的概率）

 （在C2中抽到x的概率）

有了这四个可能性P（这四个值要从training data中估出来），在test阶段，给一只神奇宝贝 x，就可以就计算它属于class 1 或class 2 的概率。 

有了这个模型，就可以生成一个 x。然后计算每个 x 出现的概率，就可以知道了 x 的分布，就可以自己产生 x  。
这就是Generative Model。

Prior

Class 1是水系，Class 2是一般系。

在training data中，从水系抽出神奇宝贝的概率  。从一般系抽出神奇宝贝的概率

 在这里，每一只神奇宝贝用一个vector代替，这个vector里面的各种值就是这只神奇宝贝的feature。

现在我们要计算从水系神奇宝贝抽出 原盖海龟 的几率，但是training data里的水系神奇宝贝没有这只原盖海龟，那怎么计算？

将training data制成图。这里的training data只是水系神奇宝贝的一部分，所以不能说原盖海龟没出现在training data里几率就等于0。

假设这些training data是从高斯分布里sample出来的一部分，所以即便原盖海龟没出现在training data，也不能说它的几率等于0。

所以现在要做的就是通过已有的79只神奇宝贝，生成这个高斯分布，从而知道从这个分布sample出原盖海龟的几率。

高斯分布

 可以把高斯分布看成一个函数，输入  一只神奇宝贝，输出  这只神奇宝贝从这个分布被sample出来的概率。

这个分布的形状由， 操纵。

• 同样的，不同的，分布的最高点不一样
• 同样的，不同的，分布的分散程度不一样

回到刚才的图，现在我们通过training data计算出  和  ，即便给出一个没出现在training data的水系神奇宝贝 x ，也可以代上面的公式  ，算出从水系神奇宝贝sample出 x 的几率。

接下来，讲一下计算  和  的方法。

我们知道79个点可以从任意一个分布sample出来，只是概率的高低而已。

图中左下角的圆圈这个分布，从这个分布sample出79个点的概率会相对高一点。

图中右上角的圆圈这个分布，从这个分布sample出79个点的概率会相对低一些。

所以，现在要找出一个分布，它sample出79个点的概率是最高。

计算某一个分布sample出79个点的计算方法 如  所示（代表是从这个分布sample出的几率，以此类推累乘下去，就是sample出79个点的概率）

 从上面高斯分布那部分知识点可以知道，分布的形状由， 操纵。所以找这个最佳的分布，其实就是找能使的值最大的，。

找到，的方法可以用图中的方法；也可以对求它对，各自的偏微分，然后各自找出偏微分等于0的点。

用这个方法，就算出刚才例子的 ，，就得到水系神奇宝贝的分布。

现在我们已经把   、、 、 都算出来，就可以算 了，即现在给出一只神奇宝贝 x ，就能算它属于C1类的概率。

如果这个概率大于0.5，就说它属于Class 1。

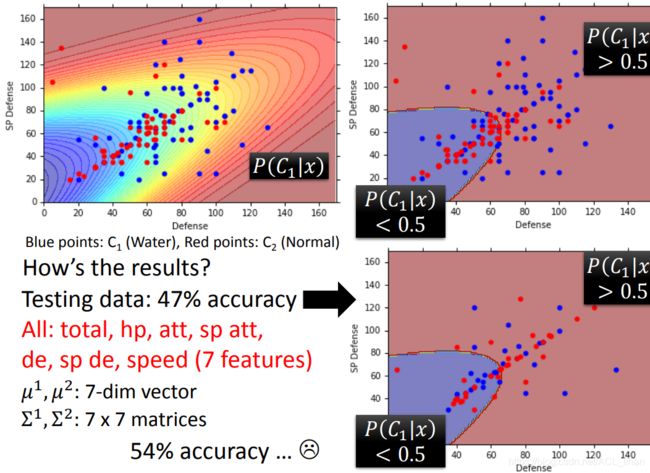
 左上图是最后做出来的分类结果。红色越深，代表越可能属于C1（水系）类；蓝色越深，代表越可能属于C2（普通系）类。

右上图是左上图做一个简化的效果，含义还是一样。

把这个model用在testing data上，结果如右下角所示。准确度只有47% 。

即便加上更多神奇宝贝的feature，如hp等，加到7维来分类，准确度也就上升到54% 。

怎么办呢？

之前的实验是两个类别分别使用各自的 ，，这样不好。因为和input的大小平方成正比（比如上面只有2个参数（SP Defense 和Defense），就有4个参数），所以当 input 变大的话，会造成参数变太多，造成variance（方差）太大，就会overfitting。

所以，为了避免这个问题，就让两个class的分布共用一个  的参数（对比原来的话就少了一个的参数）。

共用一个  后，刚才的Likelihood function 就要改写为。

的计算方法和之前一样，直接所有 x 相加取平均。类似。

 则是将原来的各自的  ， 乘上各自一个weight（eg.Class 1 就是）。

做了上面的改进后，用神奇宝贝的七个维度的feature数据来分类，准确度从54%上升73%。 

总结

其实就是找出  和  ，有了这两个参数能找到一个概率分布，这个分布能最大化 Likelihood 函数。

如果 x 有7个feature，并且都是独立的话，则  可以写成，

此时这些拆出来的项（等等）每一个都是一维的高斯分布，这时  的协方差就是一个对角矩阵（对角线之外的值都为0），这样就可以减少参数量。但在这个例子中不能这么做，因为这个例子中的 x 的feature并不是完全独立的，比如一只CP值高的神奇宝贝，他不可能HP会很低。

如果所有的feature都是相互独立的，这种分类叫做 Naive Bayes Classifier（朴素贝叶斯分类器）

在实验中，需要根据问题来选择生成的分布，比如这个例子就生成高斯分布。而在其他情况下比如二分类问题，就需要改成生成一个伯努利分布。

后验概率（Posterior Probability）

 将  做图中的变换，得到  ，这个就是Sigmoid function。

当z趋于正无穷时，趋近于1；当z趋于负无穷时，趋近于1。

接下来要算z（想了解更详细可以看视频，你也可以直接跳过看结论）：

 

 

z就等于上图所示，其中 相当于权重w，而后面很长的和 x 无关的一串相当于b。

所以也可以写成。

所以现在知道，为什么刚才在神奇宝贝分类的例子中，改进模型时使  和  相等的时候，边界线会变成是一条直线了。

 

在generative model中，我们是先算出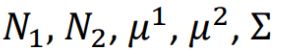，然后来得到w和b。

有没有办法直接求出w和b呢？这就是下节课的内容了