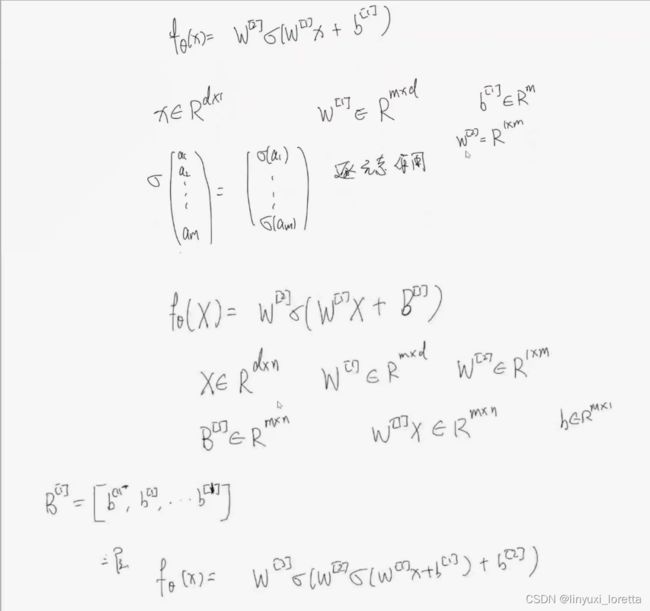2022人工智能数学基础1-2（许志钦

许老师  2017年 计算神经科学 博士后，转行做deep learning

神经元只是区分信号有无

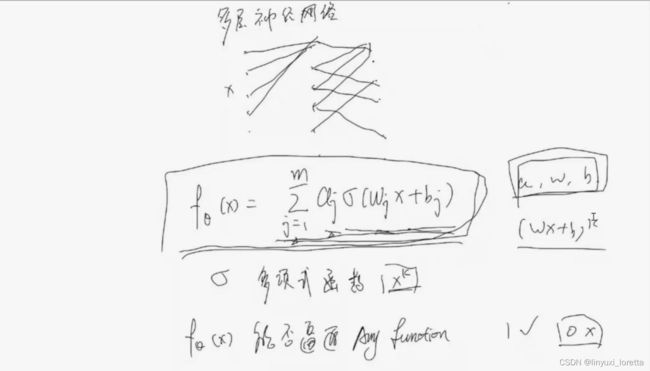
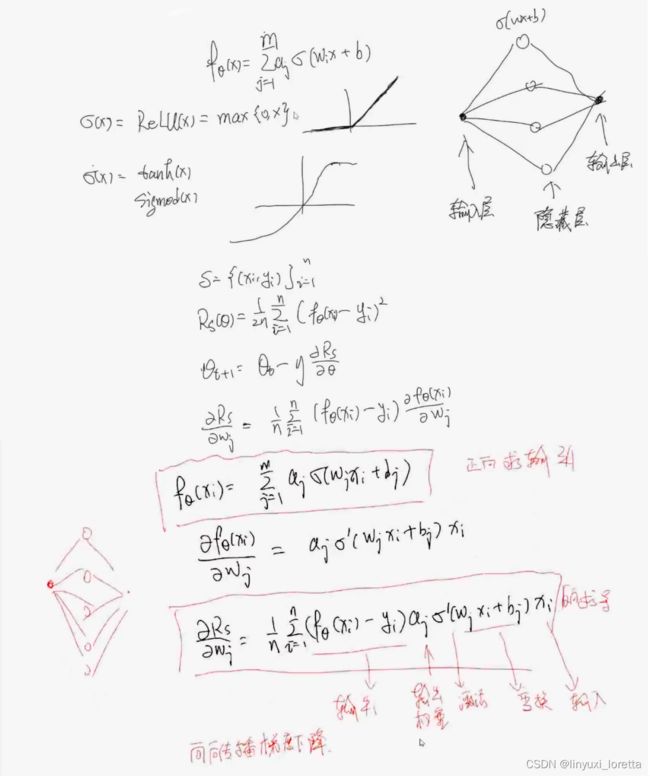
单层神经网络

 

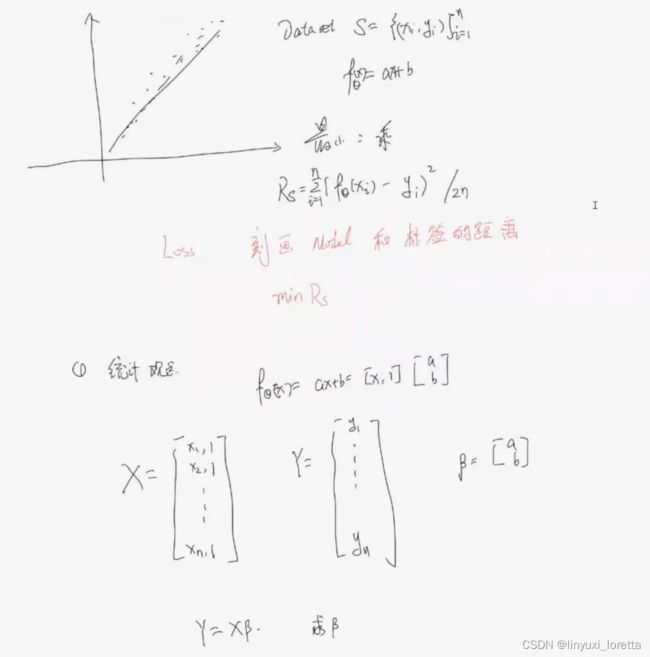
线性拟合：

 数据、有模型、算未知参数a,b 

最小二乘

定义 损失函数，    没有平方无法真正表征距离

 求β，  方法一、最小化损失函数

方法二：

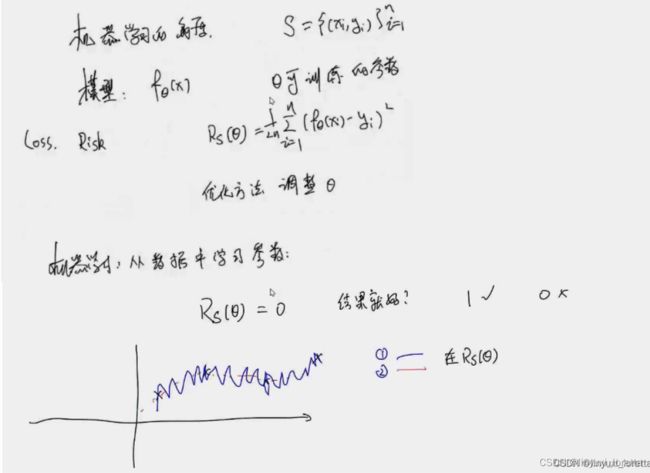
 统计角度：告诉我们 什么样的模型可用，

机器学习面临的最大困难：不知道什么时候可用，

 只知道四个点 没有办法判断， ①②哪个好

没有免费的午餐，没有一个算法比另一个绝对的好，

一般生活中的数据相对光滑，所以我们会觉得②泛化性好，

机器学习和统计的区别：统计需要理解 模型适用范围

机器学习：把数据拟合好

我们希望淡化这两者的区别

以线性拟合为例，讲解机器学习的基本概念：

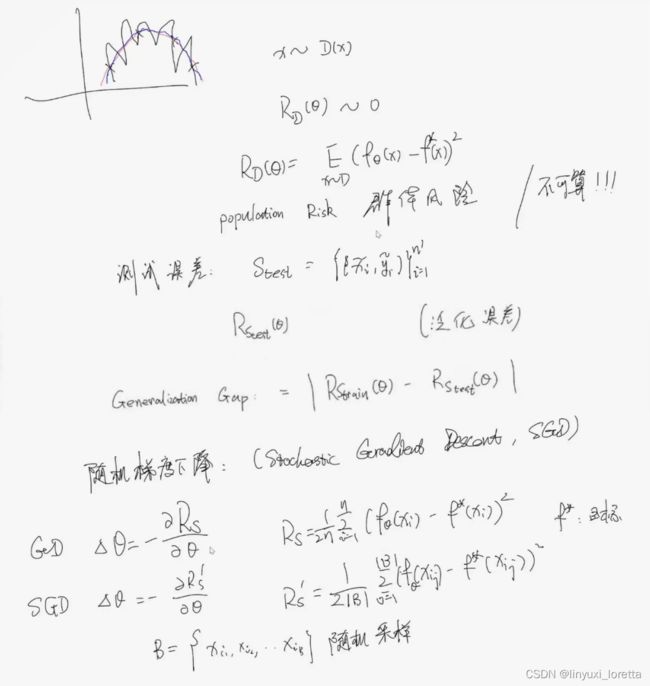
我们其实并不关心训练集的误差等于0，而是关心我们的model和真实模型匹配上

 两层神经网络

写成更一般的形式：

 n代表  数据个数，  m代表  神经元数目

b：m x 1 ，广播成B：m x n

 

 

 

 

 

 

 

 

 

 

1. 一般 多层的神经网络，写出BP（向后传播算法）20%

2. 写一个一般函数的拟合。80%

 深度学习里全都不知道...

几层网络？多少神经元？哪些激活函数？什么样的损失函数？学习率怎么调？超参怎么设？

问一些可以做的问题，比如说  误差分析

一般来说逼近误差都很小（因为参数量大），训练误差基本都能找到全局最小

 多层网络的好处？能克服高维灾难

  线性插值   和目标函数的误差？等间距采样，1维  大概是1/ n^2的收敛阶

为了降低误差，数据量得指数增长才有用

二十世纪10大算法之一，传统算法解决维度灾难，蒙特卡洛算法。但这个算法很慢

 而神经网络前面配个1/m系数，即  模型写成平均得形式，就是蒙特卡洛采样方式

---

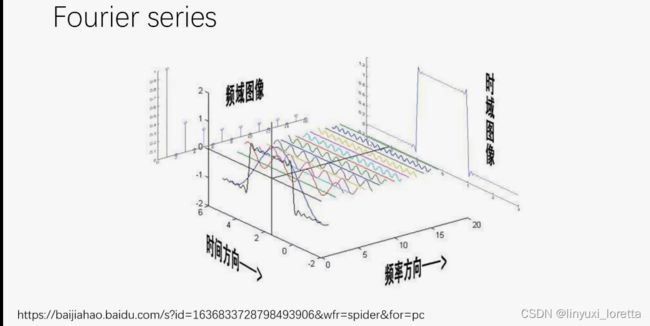
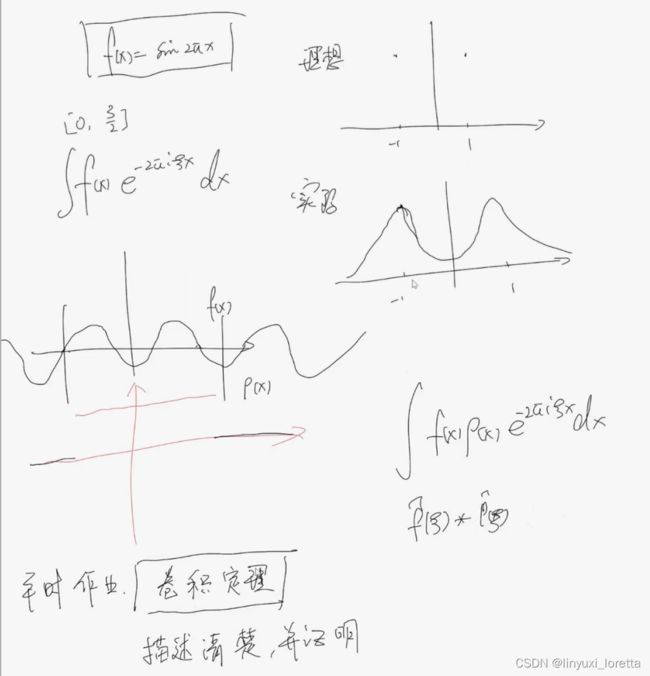
傅里叶级数

拉格朗日认为，在不连续点 会出现震荡 吉布斯现象

 频域图像    横坐标：频率 ，纵坐标：幅度 

 无限维

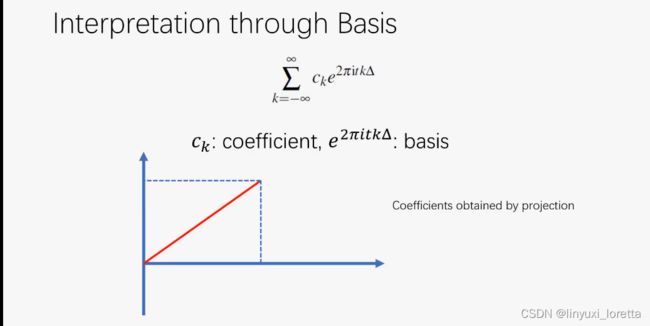
 内积就得到x轴上得投影

 

 

细节清晰、但是没有轮廓

 

发文章得技巧，关注各种量 在演化过程中的规律 ，

守恒性（比如某个量在训练过程中不变）、

单调的（演化规律，统计力学 熵增）

做研究最重要是定义一些量，然后发现这些量的规律。就对系统有了深刻的认识

进一步，解释这个现象 底层的机制、意义

海森堡 矩阵力学、薛定谔     量子力学。    “奥卡姆剃刀”同样解释一个现象 参数更少 

NIST 美国国家标准局

跳出传统思维的局限

①建模  参数多还是少？

②研究方法    图像 三维 还是更多维？   MNIST   784维，极困难

傅里叶分析  有个局限  研究低维问题

独立性：  两边同时做内积

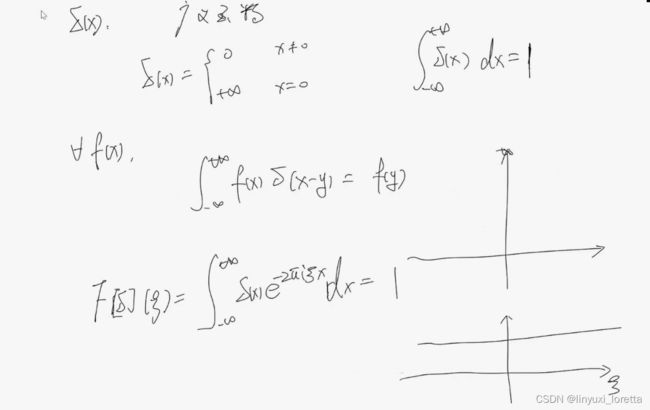
 傅立叶正变换：做投影，来找到系数。

 本质上就是把函数分解到三角函数上去研究，好处很多：cos导数-sin，sin导数cos，漂亮的周期、无穷、光滑、...

实际上 没法做连续傅里叶变换， g(x)是采样获得的，

    周期函数，周期是1/δ

 要形成稳定的驻波，周期必须是T/n,  

 FFT 二十世纪十大算法之一，O(NlnN)，速度极快

傅里叶系数的衰减特性

 中间这个表达式：抓取出 某一点的函数值

右下面图： 频率空间函数形状

 

  图片频率的幅度在衰减，  即 随着ξ（频率）变大，幅度在变小

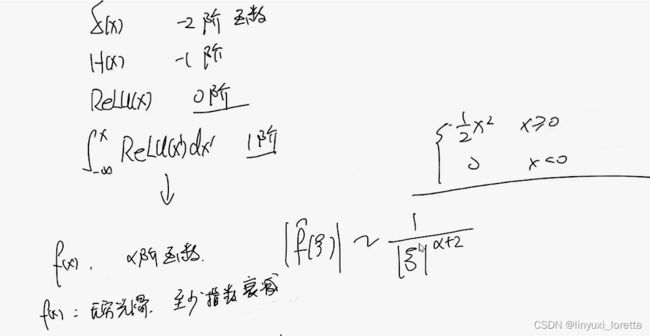
0阶可导 代表连续

  

结论：函数只要稍微光滑一点，就会随着频率衰减，

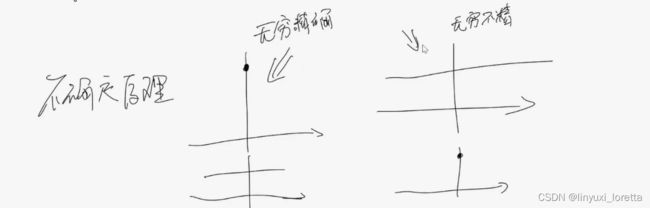
不确定性原理（诺贝尔）

 如果我们考虑x是一个空间，ξ是另一个空间，

则如果在x空间无穷快衰减，则对应的傅里叶空间 永不衰减

在一个空间越准确，在另一个空间就越不准确，

一个空间衰减越快，另一个空间衰减就越慢，

 

如果一个函数是  ，傅里叶变换后，在±1有值，其他位置都是0

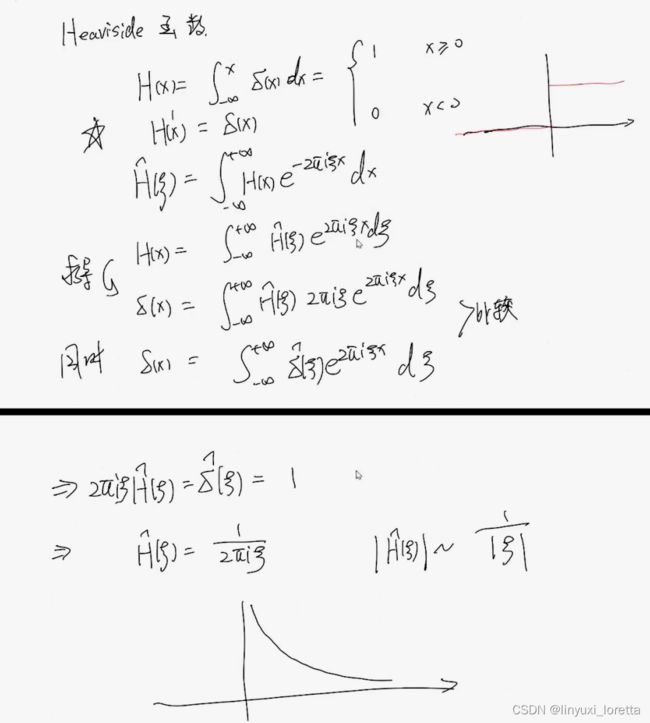
采样函数 ρ(x)，很像H(x),      

 卷积定理：相乘以后做傅里叶变换，等价于做完傅里叶变换后再做卷积

高维傅里叶变换  需要高维积分。高维积分，只能用蒙特卡洛，收敛速度很慢

看看 神经网络是什么：

1.神经网络是一个函数拟合的工具， 

2.傅里叶变换  是把一个函数转换到频率空间，频率越小的 sinx 比较平坦 光滑，频率越大sin100x 剧烈震荡。   我们需要保留这些信息

神经网络DNN 特点是参数特别多，能够拟合的好的函数中，只有一小部分可以泛化的好

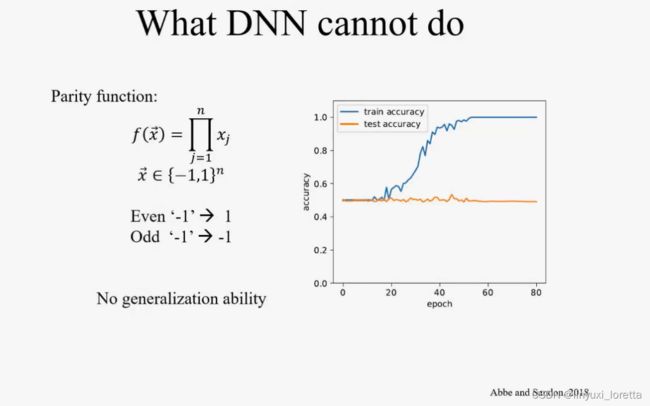
DNN的弱点：e.g. 拟合 奇偶函数

 算法符合 数据的特征 就能做好，

写文章，提出算法，在哪类问题做的好，为什么这类问题重要

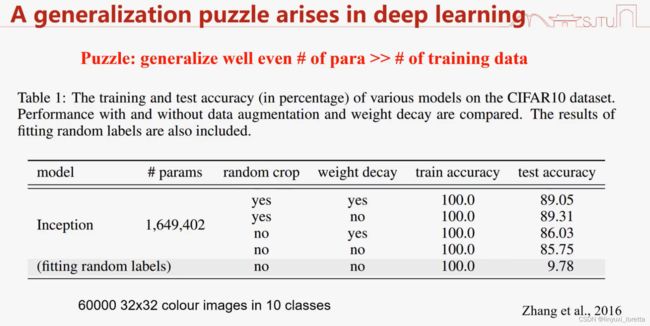
6w个数据点，160w个参数的模型来拟合，参数数目>>训练样本数，传统的学习理论会觉得肯定过拟合，

泛化谜团

 所以 看起来 神经网络并不完全可以在传统的学习理论框架下看

频率 是描述轮廓、细节、平坦、震荡的工具

频率刻画的是输出对输入的敏感程度；或者是输入变化对输出变化的影响大小，输入发生变化，输出变化很慢，低频

 纵坐标：幅度，横坐标：频率

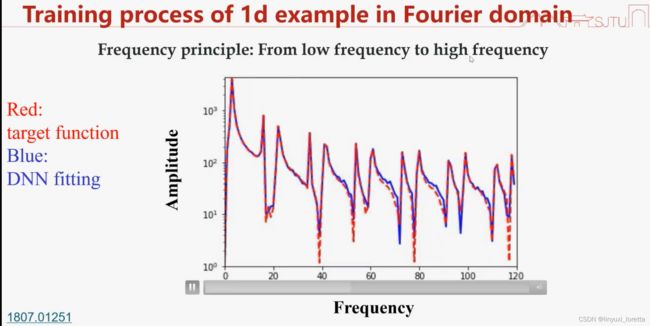
 sinx   sin3x   sin5x  幅度都一样，看相对误差下降速度

 从低频到高频的学习过程

激活函数relu，初始化比较小时，观察到 “射线”， 思考 why

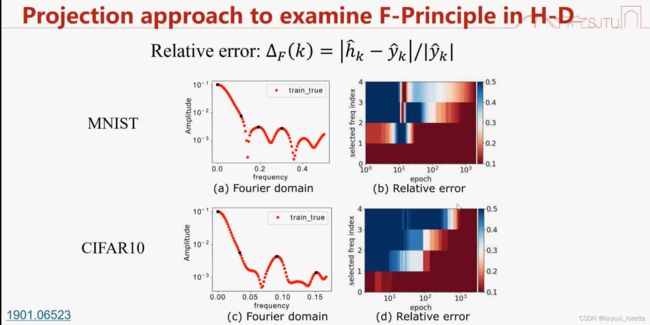
 图像分类问题，高维问题，输入是整张图片，输出是类别，

我们在前面定义的傅里叶变换里的频率，是一种input-output mapping的频率，如右边的例子，才是我们关注的频率

傅里叶解不了高维，办法：  （本质降维）

1.只看其中一维、一个截面，投影

2.所有频率的幅度 范数小于某个数就说低频，其他都说高频，相当于高维空间拿个球。

  频率空间相乘  ， 在时域空间就是卷积。   

高斯函数的傅里叶变换或逆变换还是高斯函数

在时域空间，用高斯函数和原函数做卷积（滤波），得到低频成分。也就是，卷积可以用来做滤波

观察低维，在高维验证：神经网络学 越平滑的越快越好，说的更general一点，低频比较好学，

黎曼引理：对任意一个函数 稍微光滑一点，他的傅里叶系数就是衰减的