李宏毅机器学习笔记—— 15. Network Compression( 网络压缩)
摘要: 本章主要是讲解了为什么要去做网络压缩,以及怎样去做压缩的五种方式。分别是网络剪枝,知识蒸馏,参数量化,架构设计和动态计算。(本章仅从软件方面去考虑)
网络剪枝的基本思想是先评估weight和neuron的重要性,然后把不重要的删除掉。
知识蒸馏的基本思想是训练一个大网络,用小网络(Student Net)学习大网络(teacher net)。并计算两者之间的cross-entropy,使其最小化,从而可以使两者的输出分布相近。
参数量化是从参数的存储空间角度考虑,以及权重聚类,哈夫曼编码,二元权重角度,去尽可能让参数占用更少的空间。
架构设计是用低秩近似的方法去减少参数量,但会存在缺陷;接着讲解了效果更好的深度可分离卷积。
动态计算是对CNN中间的每一层的输出进行分类,并作为结果预测,这样做也会存在很多缺陷。
文章目录
- Network Compression( 网络压缩)
- 1. Network Pruning(网络剪枝)
-
- 1.1 Network can be Pruned
- 1.2 重要性判断
- 1.3 怎么去做Network Pruning
- 1.4 why Pruning ?
- 1.5 Practical Issue(实际例子)
-
- 1.5.1 weight pruning
- 1.5.2 neuron pruning
- 2. Knowledge Distillation(知识蒸馏)
-
- 2.1 基本思想(Student and Teacher)
- 2.2 实际的技巧(Temperature)
- 3. Parameter Quantization(参数量化)
-
- 3.1 less bits
- 3.2 weight clustering
- 3.3 huffman encding(哈夫曼编码)
- 3.4 binary weights(二元权重)
- 4. Architecture Design(架构设计)
-
- 4.1 Low rank approximation(低秩近似)
- 4.2 Depthwise Separable Convolution(深度可分离卷积)
-
- 4.2.1 Depthwise Convolution(DW卷积)
- 4.2.2 Pointwise Convolution(PW卷积)
- 5. Dynamic Computation(动态计算)
-
- 5.1 Train multiple classifiers(训练大量的分类器)
- 5.2 Classifiers at the intermedia layer(用中间层输出)
- 6. 总结与展望
Network Compression( 网络压缩)
Network Compression,之所以提出模型压缩是因为我们有把Deep Model放在移动端设备(智能手表,无人机,智能机,机器人)的需求,但是这些设备上的资源是非常有限的(空间或者计算能力不足),因此要压缩空间大小、加快计算速度等。
1. Network Pruning(网络剪枝)
1.1 Network can be Pruned
神经网络的参数有很多,但其中有些参数对最终的输出结果贡献并不大,相反就显得冗余,将这些冗余的参数剪掉的技术称为剪枝。剪枝可以减小模型大小、提升运行速度,同时还可以防止过拟合。
1.2 重要性判断
那怎么评估weight或者neuron是冗余或者不重要的呢?
- 对权重(weight)而言,我们可以通过计算它的l1,l2值来判断重要程度
- 对神经元(neuron)而言,我们可以给出一定的数据集,然后查看在计算这些数据集的过程中neuron参数为0的次数,如果次数过多,则说明该neuron对数据的预测结果并没有起到什么作用,因此可以去除。
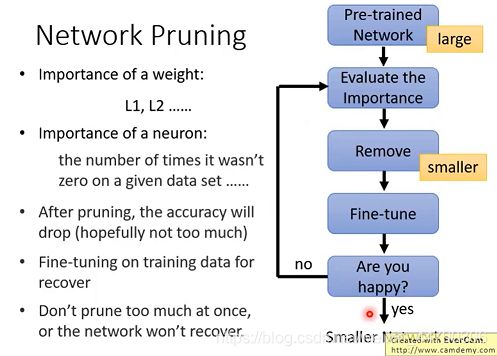
1.3 怎么去做Network Pruning
剪枝算法可分为one-shot(一次性剪枝)以及iteration(迭代剪枝):
one-shot法:首先对预先训练好的模型中神经元或权重进行重要性评估,之后剪除掉无关紧要的神经元或权重(可通过设置阈值等方法实现),再对剪枝后的模型进行微调。
而迭代剪枝可看作多次重复进行的one-shot法:在微调之后判断是否可以继续剪枝,如果可以继续进行,则再次启动one-shot法。迭代剪枝法获得的压缩模型更加紧凑,尺寸更小,但其训练成本远大于比one-shot法。
做剪枝的步骤:
- 首先要训练一个很大的模型
- 然后评估出重要的权重或神经元
- 移除不重要的权重或神经元
- 接着要对处理后的模型进行微调,进行recovery把移除的损伤拿回来。(注意不能移除太多,否则不能recovery回来)
- 结构性剪枝剪除的基本单元为神经元(卷积中为filter),由于是对神经元直接进行剪枝,结构性剪枝后的模型能够在现有硬件条件下实现明显的推理加速以及存储优势。但其缺点是剪枝的颗粒度较大,往往会对压缩后模型的精度产生较大的影响。
- 非结构剪枝剪除的基本单元为单个权重,其经过剪枝后的模型精度损失更小,但最终会产生稀疏的权重矩阵,需要下层硬件以及计算库有良好的支持才能实现推理加速与存储优势。
1.4 why Pruning ?
那我们不禁要问,既然最后要得到一个小的network,那为什么不直接在数据集上训练小的模型,而是先训练大模型 ?
-
解释一:
一个比较普遍接受的解释是因为模型越大,越容易在数据集上找到一个局部最优解,而小模型比较难训练,有时甚至无法收敛。(即只要网络结构够大,梯度下降就可以找到全局最小点) -
解释二:
2018年的一个发表的大乐透假设(Lottery Ticket Hypothesis)观察到下面的现象(但有rethinking作者说lottery仅可用于非结构化裁剪):
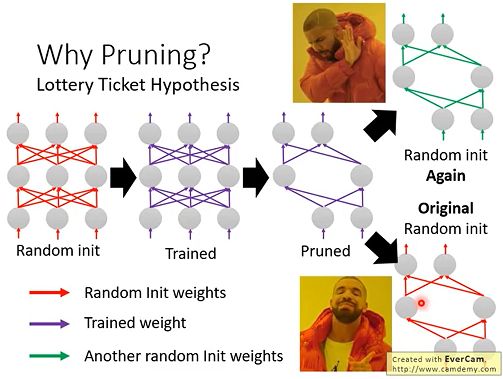
首先我们对一个大模型随机初始化它权重参数(红色)。然后我们训练这个大模型得到训练后的模型以及权重参数(紫色)。最后我们对训练好的大模型做pruning得到小模型。 -
如果我们使用pruned network的结构,再进行随机初始化random init(绿色的weight),会发现这个network不能train下去。
-
如果我们使用pruned network的结构,再使用原始随机初始化original random init(红色的weight),会发现network可以得到很好的结果。
1.5 Practical Issue(实际例子)
之前的模型pruning剪枝可以从weight和neuron两个角度进行,下面就分别介绍实际可操作性。
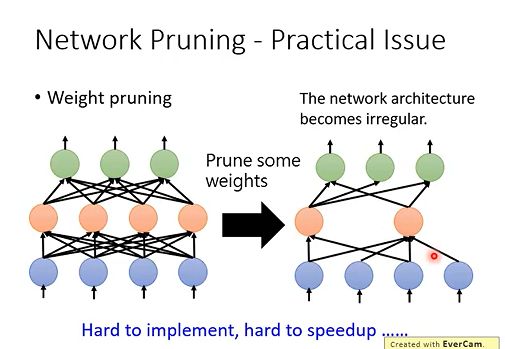
1.5.1 weight pruning
- 如果我们现在进行weight pruning,进行weight pruning之后的network会变得不规则(每个节点的输出和输出节点数都会变得不规则),这样的network是不好implement出来的
- GPU是对矩阵运算做加速,现在都变得不规则,并不能使用GPU加速。(实际的方法是将pruning的weight写成0,仍然在做矩阵运算,仍然可以使用GPU进行加速;但这样也会带来一个新的问题,我们并没有将这些weight给pruning掉,只是将它写成0了而已)
1.5.2 neuron pruning
如下图所示,删减neuron之后网络结构能够保持一定的规则,实现起来方便,而且也能起到一定的加速作用。
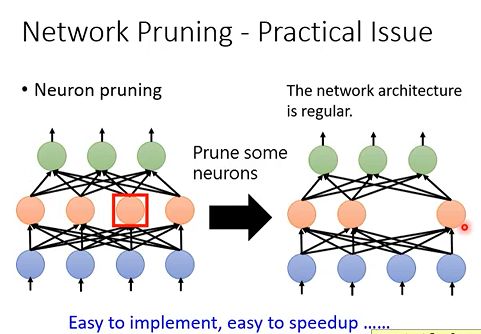
通过上述可知,实际上做weight pruning是很麻烦的,通常我们都进行neuron pruning,可以更好地进行implement,也很容易进行speedup。
2. Knowledge Distillation(知识蒸馏)
2.1 基本思想(Student and Teacher)
整个知识蒸馏过程中会用到两个模型:大模型 Teacher Net 模型和小模型Student Net模型。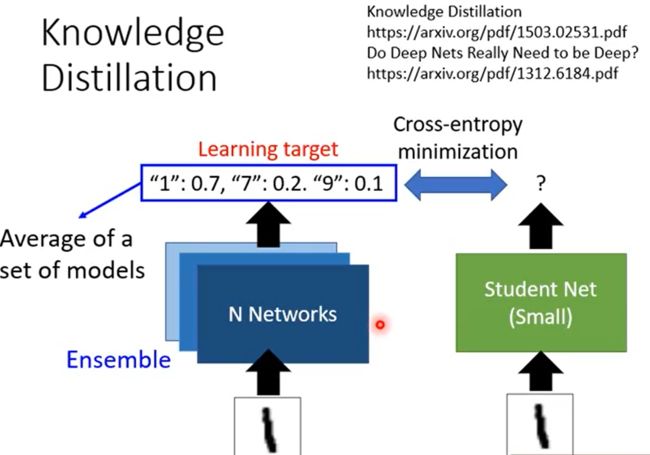
训练一个大网络,用小网络(Student Net)学习大网络(teacher net)。并计算两者之间的cross-entropy,使其最小化,从而可以使两者的输出分布相近。
由teacher提供了比label data更丰富的资料,比如teacher 模型不仅给出了输入图片和1很像的结果,还说明了1和7长得很像,1和9长得很像;所以,student跟着teacher net学习,是可以得到更多的information的。
当然,一个更好的办法就是让多个老师出谋划策来教学生,即用Ensemble Net来进一步提升预测准确率,让学生学习的知识更加准确。
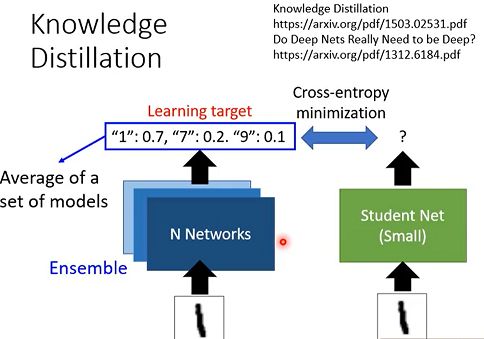
2.2 实际的技巧(Temperature)
那么Student Net 是如何学习的呢?首先回顾一下在多类别分类任务中,我们用到的是softmax来计算最终的概率(softmax函数,又称归一化指数函数,它是二分类函数sigmoid在多分类上的推广,目的是将多分类的结果以概率的形式展现出来),即公式形式: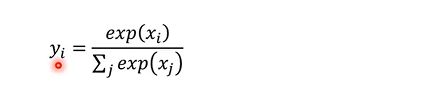
但是这样有一个缺点,因为使用了指数函数,如果在使用softmax之前的预测值是x1=100,x2=10,x3=1,那么使用softmax之后三者对应的概率接近于y1=1,y2=0,y3=0,那这和常规的label无异了,所以为了解决这个问题就引入了一个新的参数T,称之为Temperature即:
 这样做的话,如果我们令T=100,那么最后的预测概率是y1=0.56,y2=0.23,y3=0.21(预测概率会有区分),如下图:
这样做的话,如果我们令T=100,那么最后的预测概率是y1=0.56,y2=0.23,y3=0.21(预测概率会有区分),如下图:

这个实际做法,其实呢,并没有什么作用!!!
3. Parameter Quantization(参数量化)
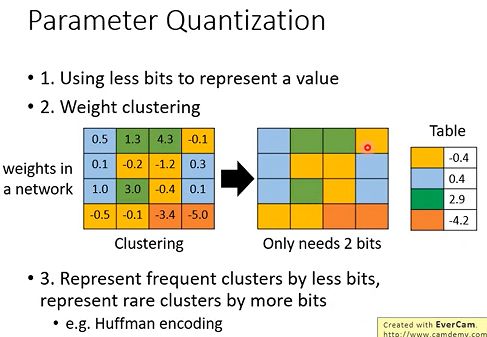
3.1 less bits
最直观的方法:使用更少bit来存储数值(参数),例如一般默认是32位,那我们可以用16或者8位来存数据。
3.2 weight clustering
如上图所示,最左边表示网络中正常权重矩阵,之后我们对这个权重参数做聚类,比如将16个参数做聚类,最后得到了4个聚类,那么为了表示这4个聚类我们只需要2个bit,即用00,01,10,11来表示不同聚类。之后每个聚类的值就用均值来表示。这样的一个缺点就是误差可能会比较大。
3.3 huffman encding(哈夫曼编码)
基本思想:对于常出现的聚类用少一点的bit来表示,而那些很少出现的聚类就用多一点的bit来表示。
3.4 binary weights(二元权重)
Binary Weights是以一种更加极致的思路来对模型进行压缩,即每个节点只用1或-1来表示,即只用+1,-1表示一个Weight。
下面简单介绍一下Binary Connect的思路,如下图示,灰色节点表示使用binary weight的神经元,蓝色节点可以是随机初始化的参数,也可以是真实的权重参数。
- 第一步我们先计算出和蓝色节点最接近的二元节点,并计算出其梯度方向(红色剪头)
- 第二步,蓝色节点的更新方向则是按照红色箭头方向更新,而不是按照他自身的梯度方向更新。
- 最后在满足一定条件后(例如训练之最大次数),用离得最近的Binary Weight(二元权重)作为结果即可。
从结果上看还是不错的,可以看到把权重限制为+1或者-1相当于加上了正则化,但还是比不过Dropout方式!
4. Architecture Design(架构设计)
4.1 Low rank approximation(低秩近似)
下图是低秩近似的简单示意图,左边是一个普通的全连接层,可以看到权重矩阵大小为M×NM×N,而低秩近似的原理就是在两个全连接层之间再插入一层K。是不是很反直观?插入一层后,参数还能变少? 那么这样会带来什么影响呢?那就是原先全连接层能表示更大的空间,而现在只能表示小一些的空间,会限制原来的NN能做的事情。 从标准卷积CNN中看所需要的参数量。如上图示,输入数据由两个 6 ∗ 6 6*6 6∗6的feature map组成,之后用4个大小为 3 ∗ 3 3*3 3∗3的卷积核做卷积,最后的输出特征图大小为4个 4 ∗ 4 4*4 4∗4的矩阵。每个卷积核参数数量为233=18,所以总共用到的参数数量为4*18=72个。 Depthwise Separable卷积分成了两步: 将立体的,深度为2的filter分成两个平面的,不考虑之间的联系(每个卷积核只考虑一个通道),然后分别对一个feature map进行卷积,得到下图结果: 为了实现关联,在第二步中使用了 1 ∗ 1 1∗1 1∗1大小的卷积核,并且通道数量等于输入数据的通道数量,然后按照正常的CNN做法,得到结果4个 4 ∗ 4 4*4 4∗4的矩阵,如图: 该方法的主要思路是如果目前的资源充足(比如你的手机电量充足),那么算法就尽量做到最好,比如训练更久,或者训练更多模型等;反之,如果当前资源不够(如电量只剩10%),那么就先算出一个过得去的结果。 那么如何实现呢? 需要我们提前训练多种网络(从小到大),比如小网络,中等网络,大网络,那么我们就可以根据资源情况来选择不同的网络。但是这样的缺点是我们需要保存多个模型,这在移动设备上的可操作性不高。 这样的思路其实也挺直观的,就是比如说我们做分类任务,当资源有限时,我们可能只是基于前面几层提取到的特征做分类预测,但是一般而言这样得到的结果会打折扣,因为前面提取到的特征是比较浅的,可能只是一些纹理,而不是比较高层次抽象的特征。 本章主要学习的Network Compression的几种方法,分别从各个方面对网络进行压缩:从减少网络参数和神经元个数角度可以考虑Network Pruning方法,通过训练一个大的网络,修剪掉其中weight接近0的参数或神经元;从压缩参数角度考虑可以使用Parameter Quantization方法,采用更小的bit来代替参数值和将weight分组后进行取平均值代替每组的weight;从调整网络结构角度考虑可以使用Architecture Design方法,在两个很大的神经元之间增加一层较少神经元的中间层,可以减少需要的参数等。但是由于Compression压缩的方法不是独立的,组合使用多种上面的压缩方法,可能会比单独使用一种压缩方法的效果更佳!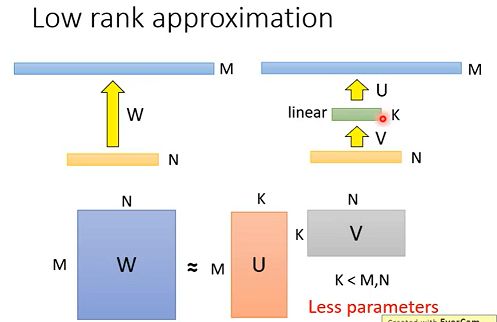
我们可以用发现这个新插入一层后的参数数量为: N×K+K×M=K×(M+N),因为K
4.2 Depthwise Separable Convolution(深度可分离卷积)
4.2.1 Depthwise Convolution(DW卷积)
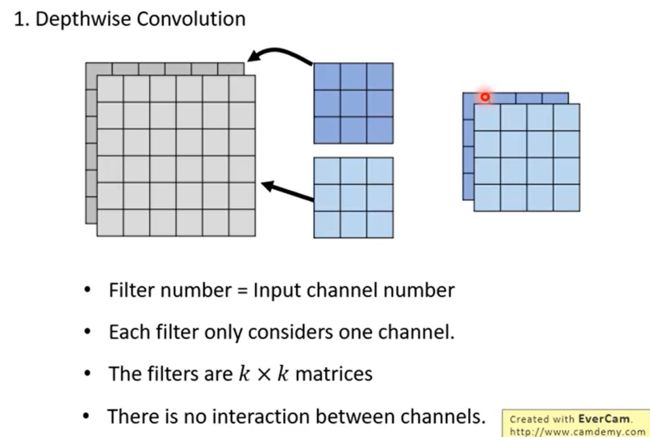
由于第一步得到的输出特征图是用不同卷积核计算得到的,所以不同通道之间是独立的,因此我们还需要对不同通道之间进行关联。4.2.2 Pointwise Convolution(PW卷积)
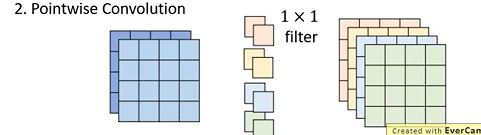
并且做深度可分离卷积的过程参数数量比标准的CNN更少:
18+8=26(共用了26个参数)
5. Dynamic Computation(动态计算)
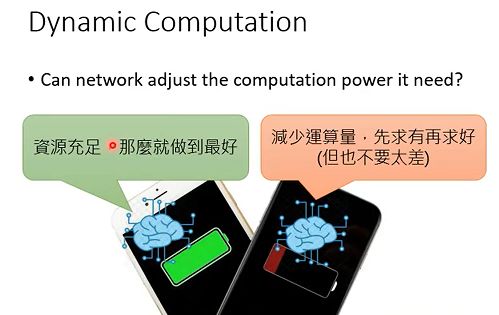
5.1 Train multiple classifiers(训练大量的分类器)
5.2 Classifiers at the intermedia layer(用中间层输出)

两个缺陷:


6. 总结与展望