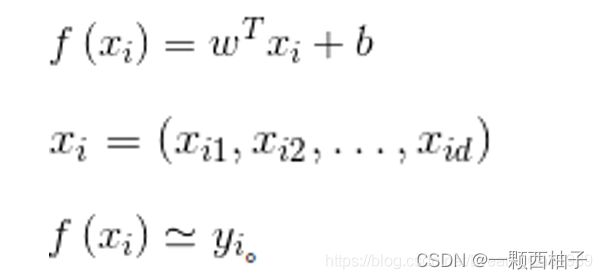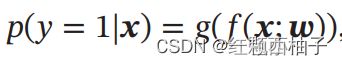新手入门机器学习案例（附源代码）

这里复习一下一些简单的机器学习算法，也算是一个总结，希望能给大家做一个参考，后续会继续更新。

基础知识

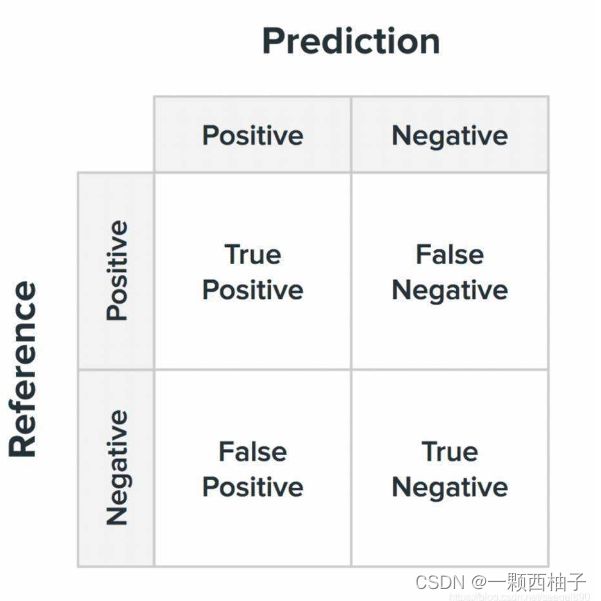
混淆矩阵

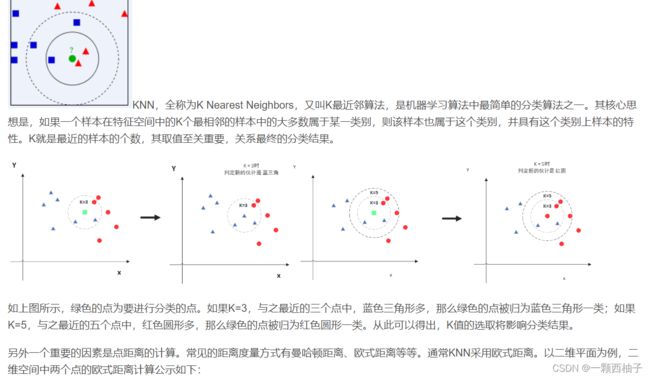
第一天-KNN

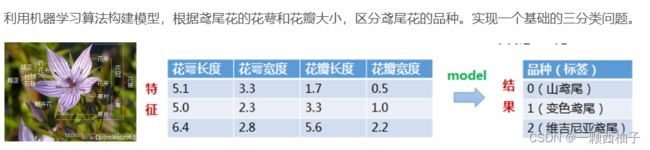
鸢尾花分类

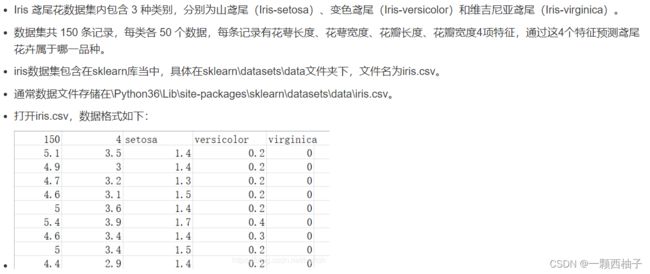
数据集介绍

代码实现

import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score

iris_data = load_iris()

print("花的样本数量：{}".format(iris_data['data'].shape))

# 构造训练数据和测试数据
X_train, X_test, y_train, y_test = train_test_split(
    iris_data['data'], iris_data['target'], random_state=0)
print("训练样本数据的大小：{}".format(X_train.shape))
print("训练样本标签的大小：{}".format(y_train.shape))
print("测试样本数据的大小：{}".format(X_test.shape))
print("测试样本标签的大小：{}".format(y_test.shape))

# 构造KNN模型
knn = KNeighborsClassifier(n_neighbors=5)

# 训练模型
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)

# 评估模型
print("模型精度：{:.2f}".format(np.mean(y_pred == y_test)))
print("模型精度：{:.2f}".format(knn.score(X_test, y_test)))

# 查看模型情况
prediction = knn.predict(X_test)
print(confusion_matrix(y_test, prediction))
print(classification_report(y_test, prediction))
print(accuracy_score(y_test, prediction))

补充说明

KNN算法

第二天-线性回归

波士顿房价预测

波士顿房价预测介绍

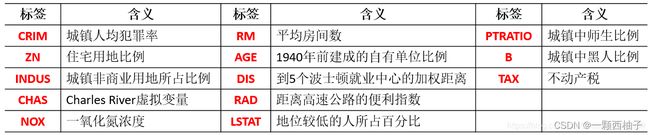
问题描述：波士顿房价数据集统计的是20世纪70年代中期波士顿郊区房价的中位数，统计了城镇人均犯罪率、不动产税等共计13个指标，统计出房价，试图能找到那些指标与房价的关系。数据集中一共有506个样本，每个样本包含13个特征信息和实际房价，波士顿房价预测问题目标是给定某地区的特征信息，预测该地区房价，是典型的回归问题（房价是一个连续值）。波士顿房价数据集中主要的指标名称及其含义如下。

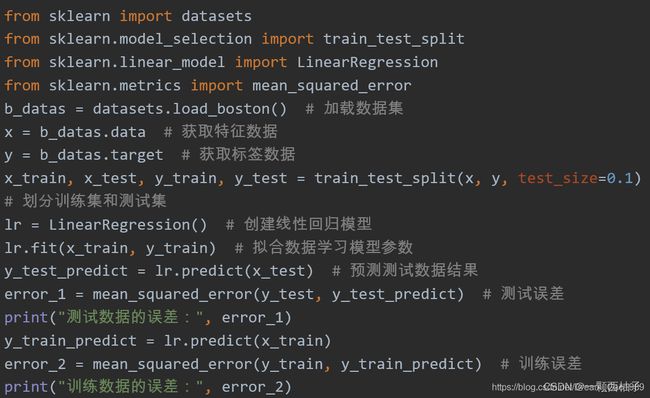
机器学习库scikit-learn中自带了波士顿房价数据集，可直接加载。房价预测可采用线性回归算法。

线性回归算法

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，通过属性的线性组合进行预测的线性模型，其目的是找到一条直线或者一个平面或者更高维的超平面，使得预测值与真实值之间的误差最小化。

线性回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。线性回归算法的公式如下，xi表示样本，可以是多维的，w为系数矩阵，b为偏置。目标是学习w和b两个参数，使得计算结果和真实结果之间的误差最小。

代码实现

第三天-支持向量机

什么是支持向量机

因为这个算法的关键点就是支持向量，那么，什么叫支持向量呢？ 就是离分割超平面(在二维中叫做分割线)最近的那些点。

看上面这个图，中间的实线就是分割超平面，两个虚线所经过的点就是支持向量。这时候大家可能又有疑问了，图b 和图c有什么区别呢？
我们可以看到，图b分割虚线和实线之间的距离比较大，而图c分割虚线和实线之间的距离比较小。SVM要找的就是使间隔最大。

鸢尾花分类

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
import numpy as np
iris = datasets.load_iris()
# 因为是二维数据，所以取出两个特征
X = iris.data[:, [2, 3]]
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3,random_state=0)
# 标准化
sc = StandardScaler()
X_train_std=sc.fit_transform(X_train)
X_test_std= sc.fit_transform(X_test)

# 画图
def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
    # 设置marker generator和color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                           np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim = (xx2.min(), xx2.max())
    X_test, y_test = X[test_idx, :], y[test_idx]
    for idx, cl in enumerate(np.unique(y)):  # np.unique:去除重复数据
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl)
    if test_idx:
        X_test, y_test = X[test_idx, :], y[test_idx]
        plt.scatter(X_test[:, 0], X_test[:, 1], c='black', alpha=0.8, linewidths=1, marker='o', s=10, label='test set')

# 将训练集和测试集合并
X_combined_std = np.vstack((X_train_std, X_test_std))
y_combined = np.hstack((y_train, y_test))
svm = SVC(kernel='linear', C=1.0, random_state=0)# 使用线性核函数，设置C值为1
svm.fit(X_train_std, y_train)
plot_decision_regions(X_combined_std, y_combined, classifier=svm, test_idx=range(105,150))
plt.xlabel('petal length {standardized}')
plt.ylabel('petal width {standardized}')
plt.legend(loc='upper left')
plt.show()

第四天-逻辑回归

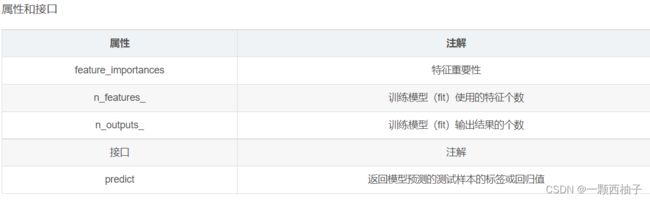
sklearn中参数解释

逻辑回归能够解决什么？

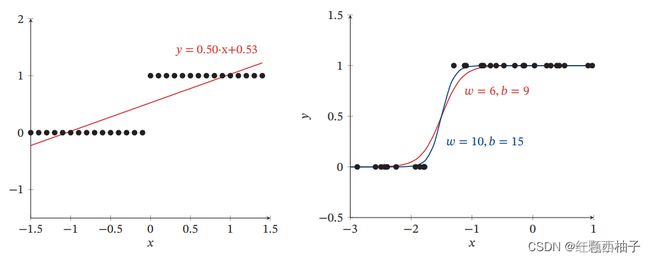
逻辑回归可以很好的解决连续的线性函数无法很好的分类的问题，如图所示，左侧为线性回归，右侧为逻辑回归。

公式

p的含义为输入x为类别1的概率，其中因为是二分类，那么0和1的概率和为100%。f(x;w)为连续的线性函数，其中g(x)是激活函数，将f()函数的值映射到（0，1）区间，这样图像看起来是个非线性的，本质上是个线性函数。

乳腺癌预测

from sklearn.linear_model import LogisticRegression
from sklearn import datasets 
from sklearn.model_selection import train_test_split

data=datasets.load_breast_cancer() # 乳腺癌数据集
X =data['data'] #数据
Y = data['target'] #标签
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=0.3,random_state=1) #划分测试集和训练集
#配置逻辑回归，penalty为正则化，solver为求解w的方法
l1 = LogisticRegression(penalty="l1",C=0.5,solver="liblinear") 
l1.fit(X_train,Y_train)
y_predict = l1.predict(X_test)
print(y_predict)
score =  l1.score(X_test,Y_test)
print(score)

第n天-决策树

糖尿病预测

kaggle数据集，有些同学可能不方便，已经给大家下好了。
数据集

决策树（Decision tree）是一种非参数的有监督学习方法，它能够从一系列有特征的和标签的数据中总结出决策规则，并以树状图的结构来呈现这些规则，以解决分类和回归问题。

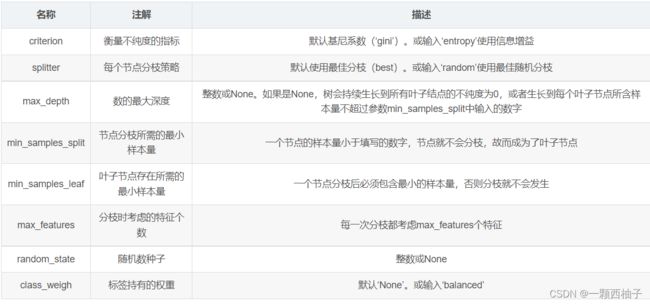
决策树参数

from sklearn.tree import DecisionTreeClassifier

clf=DecisionTreeClassifier()
clf=clf.fit(x_train,y_train)
result=clf.score(x_test,y_test)