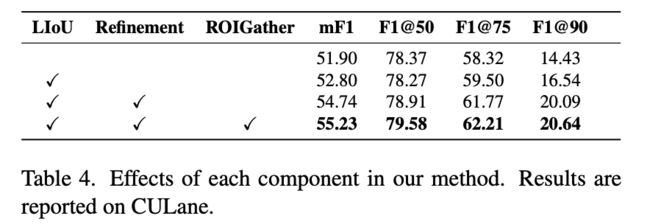
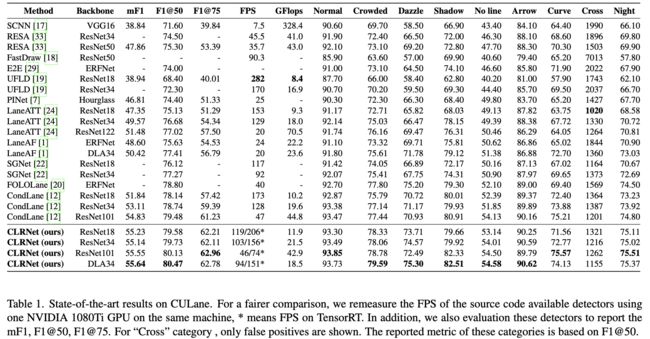
《CLRNet:Cross Layer Refinement Network for Lane Detection》论文笔记
参考代码:CLRNet
1. 概述
介绍:车道线检测任务是一种高低层次信息都依赖的任务,在CNN网络的高层次特征具有较强的抽象表达能力,可以更加准确判别是否为车道线。而在CNN网络的低层次特征中包含丰富输入图像纹理信息,可以帮助车道线进行更精准定位。而在这篇文章中提出了一种级联优化(从高层次的特征到低层次的特征)的车道线检测算法,极大限度利用了高低维度的特征去优化车道线在高分辨率下的预测准确度。不同与之前的LaneeATT中直接特征index的方案,这篇文章中提出了基于双线性采样的线型RoI提取算子(ROIGather)。此外,文章构建整体维度的Lane IoU loss约束整体车道线的回归质量。
在车道线检测任务中会存在各式各样的问题,最为典型的就是下图中所示的4中情况:
- a)车道线本身存在奇异,导致训练回归的目标也存在不唯一性;
- b)车道线的偏移量回归不准确,导致在上采样的过程中存在偏移的问题;
- c, d)由于遮挡、极限光照条件、车道线磨损等情况导致车道较难检测;
对于上述的(a,c,d)可以通过高维度的语义信息进行解决,而b中的细节信息可以通过使用低维度的语义信息进行细致优化。而这篇文章正是很好使用高维和低维级联优化与优势互补实现车道线的高精度定位。
2. 方法设计
2.1 网络结构
文章提出的网络结构见下图所示:
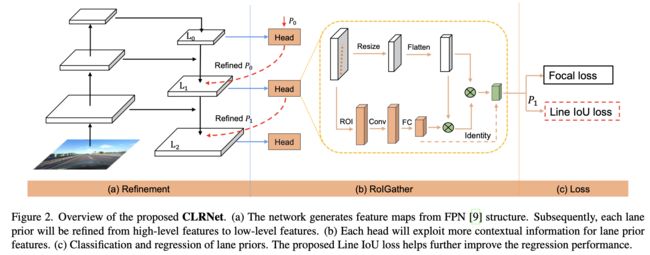
参考上图可以看到文章中的方法使用一个FPN网络去提取图像特征,之后在每个特征stage上去优化车道线的回归结果,而当前stage的回归结果会被下一阶段的细致优化所采用,从而实现车道线的级联优化。
对于上述提到的级联优化策略,文章中给出了各式组合优化的比较:
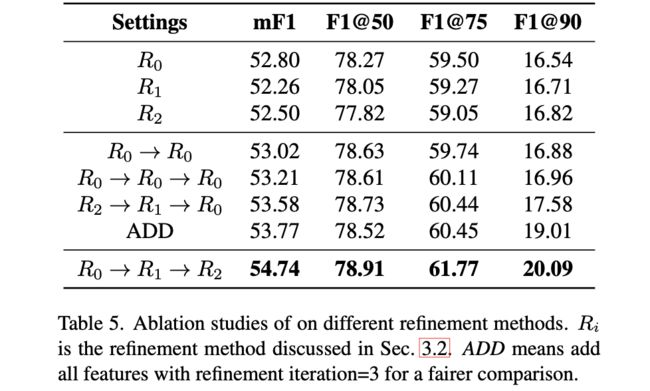
说明从高层次特征开始往低层次特征进行优化带来的收益是最大的。
2.2 车道线建模
这里车道线的建模是采用的点集的形式 P = { ( x 1 , y 1 ) , … , ( x N , y N ) } P=\{(x_1,y_1),\dots,(x_N,y_N)\} P={(x1,y1),…,(xN,yN)},也就是可以描述为在Y轴上进行均匀采样的形式: y i = H N − 1 ∗ i y_i=\frac{H}{N-1}*i yi=N−1H∗i(这里的 N = 72 N=72 N=72),再加上车道线与X轴的夹角 θ \theta θ(初始的时候可通过数据分析确定),文章对此将其称之为Lane Prior(可以理解为anchor box)。那么文章需要回归的量就包含了4个部分:
- 1)是否为车道线的类别信息;
- 2)车道线的长度;
- 3)车道线的起始点坐标 ( x , y ) (x,y) (x,y)和车道线prior与X轴的夹角 θ \theta θ;
- 4)与划分点数量 N = 72 N=72 N=72相对应的位置回归量;
2.3 ROIGather
在给定Lane Prior(会根据回归所在stage的不同, θ \theta θ会发生变化)下参考RoIAlign操作使用双线性差值的方式在prior上均匀采样得到 N p = 36 N_p=36 Np=36个采样点,这些采样点的集合就是 X p ∈ R C ∗ N p X_p\in R^{C*N_p} Xp∈RC∗Np。同时,对应stage的特征会经过维度变换得到 X f ∈ R C ∗ H W X_f\in R^{C*HW} Xf∈RC∗HW的特征,将其与采样点集合进行attention权重计算(更有效获取上下文信息):
W = f ( X p T X f C ) \mathcal{W}=f(\frac{X_p^TX_f}{\sqrt{C}}) W=f(CXpTXf)
其中, f = s i g m o i d ( ⋅ ) f=sigmoid(\cdot) f=sigmoid(⋅)操作。那么最后RoIGather操作输出的特征描述为:
g = X p + W X f T \mathcal{g}=X_p+\mathcal{W}X_f^T g=Xp+WXfT
其计算的过程可以具体参考上图2中的中间部分。需要注意的是当前stage上的RoI feat会与之前stage的RoI feat进行channel-wise的concat操作由于优化现有特征,ref:issue4
2.4 Line IoU loss
参考在目标检测和语义分割中的IoU计算方式,这里对车道线预测在row-wise进行IoU扩展。也就是计算在一定列范围内的重叠度,也就是如下的形式:
I o U = d i o d i u = min ( x i p + e , x i g + e ) − max ( x i p − e , x i g − e ) max ( x i p + e , x i g + e ) − min ( x i p − e , x i g − e ) IoU=\frac{d_i^o}{d_i^u}=\frac{\min(x_i^p+e,x_i^g+e)-\max(x_i^p-e,x_i^g-e)}{\max(x_i^p+e,x_i^g+e)-\min(x_i^p-e,x_i^g-e)} IoU=diudio=max(xip+e,xig+e)−min(xip−e,xig−e)min(xip+e,xig+e)−max(xip−e,xig−e)
其中, p , g , e = 15 p,g,e=15 p,g,e=15分别代表预测结果、GT、左右扩展的半径。则在Y轴上有 N = 72 N=72 N=72个采样的点那么整体Lane的IoU描述为:
L I o U = ∑ i N d i o ∑ i N d i u LIoU=\frac{\sum_i^Nd_i^o}{\sum_i^Nd_i^u} LIoU=∑iNdiu∑iNdio
则对应的Lane IoU loss被描述为:
L L I o U = 1 − L I o U L_{LIoU}=1-LIoU LLIoU=1−LIoU
这里提出的损失函数与Smooth L1损失函数带来的性能差异:

2.5 Match Strategy
产生了很多的lane prior对应的预测结果,那么它是如何与GT进行匹配的呢?这里是通过计算分类代价和几何相似性得到的,其匹配的代价被描述为:
C a s s i g n = w c l s C c l s + w s i m C s i m C_{assign}=w_{cls}C_{cls}+w_{sim}C_{sim} Cassign=wclsCcls+wsimCsim
其中, C c l s C_{cls} Ccls就是分类匹配的代价,而结构相似性的匹配代价被描述为:车道线起始点 C x y C_{xy} Cxy差异、车道线角度差异 C θ C_{\theta} Cθ、车道线上采样点平均距离差异 C d i s C_{dis} Cdis。其组合为:
C s i m = ( C x y ⋅ C θ ⋅ C d i s ) 2 C_{sim}=(C_{xy}\cdot C_{\theta} \cdot C_{dis})^2 Csim=(Cxy⋅Cθ⋅Cdis)2
另外, w c l s = 1 , w s i m = 3 w_{cls}=1,w_{sim}=3 wcls=1,wsim=3。
2.6 Loss
整体的损失函数是由3个分布的损失函数组合得到的:
L t o t a l = w c l s L c l s + w l x y θ L l x y θ + w L I o U L L I o U L_{total}=w_{cls}L_{cls}+w_{lxy\theta}L_{lxy\theta}+w_{LIoU}L_{LIoU} Ltotal=wclsLcls+wlxyθLlxyθ+wLIoULLIoU
其中, L l x y θ L_{lxy\theta} Llxyθ代表的是车道线长度、起始点、角度的损失。