数据结构6----带头双向循环链表的实现

数据结构(六)—带头双向循环链表

链表的分类

链表可以由以下特征来分类：

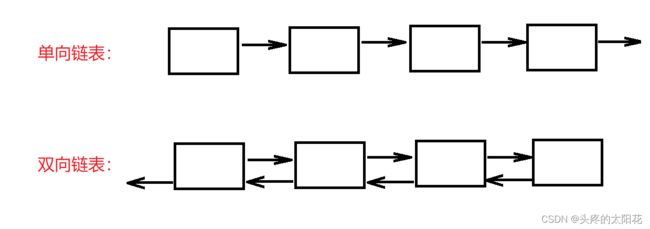
1. 单向链表还是双向链表：

   双向链表中的每一个节点除了有一个指向下一个节点的指针外，还有一个指向上一个节点的指针。

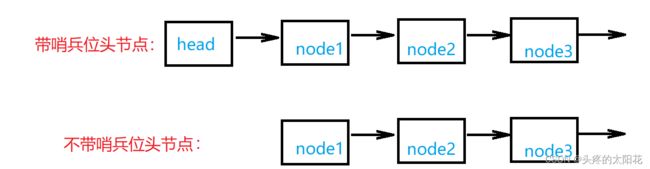
2. 是否带有哨兵位头节点：

   哨兵位节点是用来存储第一个节点的地址的。

3. 是否循环：
   循环链表的最后一个节点的next指针指向第一个节点

按照上面的三个条件就可以分为八种链表（2的三次方）。

前面我们已经介绍了单向、不带哨兵位、非循环的链表（最简单的链表结构），这一期我们会介绍双向带头循环链表（最复杂的链表结构）。

带头双向循环链表的结构

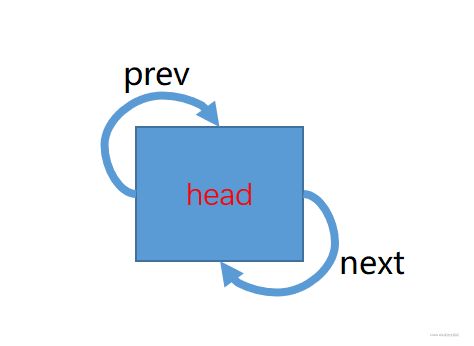
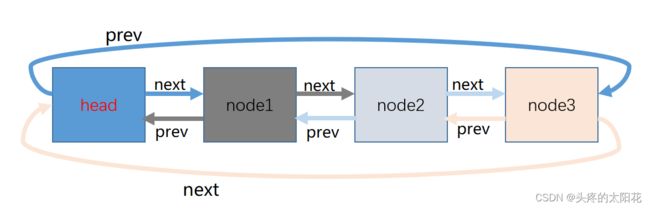
带头双向循环链表的节点中比较特殊的是它有两个指针，一个指针prev指向前一个节点，一个指针next指向后一个节点。

由于该链表带有哨兵位，所以无论有没有要存储的数据，都会存在一个节点，这个节点还应该满足循环的条件。

空链表的状态：

非空链表的状态：

带头双向循环链表的实现

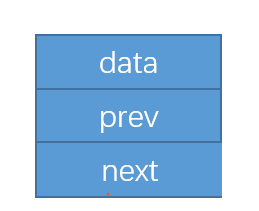
节点结构的定义：

每一个节点都有一个指向上一个节点的指针和一个指向下一个节点的指针。

//存储数据类型重定义
typedef int LTDataType;

//节点结构的定义
typedef struct ListNode {
	LTDataType data;
	struct ListNode* prev;//指向前一个节点
	struct ListNode* next;//指向后一个节点
}ListNode;

初始化链表：

我们可以在初始化链表的函数中创建哨兵位头节点，然后返回这个节点的地址

ListNode *InitList();
//初始化不用参数，将哨兵位节点返回

ListNode* InitList()
{
	//创建一个头节点，初始化改头节点
	ListNode* head = (ListNode*)malloc(sizeof(ListNode));
	if (head == NULL)//判断是否空间申请成功
	{
		printf("malloc head:fail");
		return 0;
	}
	//head就是头节点的地址

	head->data = 0;
	head->next = head;
	head->prev = head;
	//由于是带头双向循环链表，所以在链表中没有元素的时候，指向下一个节点的指针和指向上一个节点的指针的=都指向自己

	//返回头结点的地址
	return head;
}

注意，在创建哨兵位节点的时候一定要指定prev和next指针指向这个节点本身，否则就无法形成循环

我们一般创建一个指针来保存该函数的返回值。

int main()
{
    ListNode *phead = InitList();
    //现在phead就是哨兵位的地址
    return 0;
}

思考：有些地方说双向链表中的头节点data值可以用来表示节点的个数（即存放整形数据），但是这该链表的数据类型可以是char类型，也可以是double类型，所以只能在存放的数据类型是int类型的时候才能用来表示节点的个数。

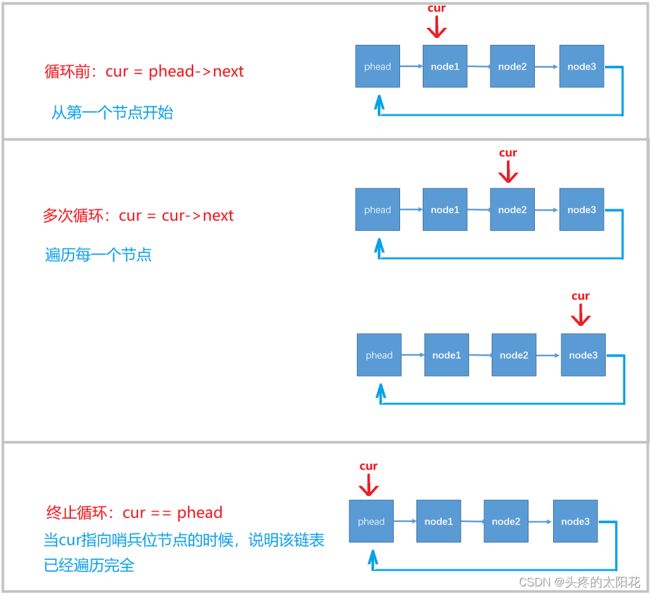
遍历链表

要想得到链表中的所有数据，仍然只有遍历链表这一种方法，但是由于这个链表的特殊性（带头、循环），我们判断遍历完全的条件就不再是遍历当指针为空，而是当遍历的指针指向头节点的时候，判断出已经遍历完全改链表。

ListNode *cur = phead->next;
while(cur != phead)//当指针指向头节点的时候循环终止
{
    
    //...;//遍历链表时需要执行的操作
    
    cur = cur->next;//指针指向下一个节点
}

注意：cur指针的值一定是哨兵位的下一个节点，如果cur保存的是哨兵位的地址，那么就不会进入循环。

打印整个链表

void ListPrint(ListNode *phead);

在遍历链表的时候打印出各个节点的值

void ListPrint(ListNode *phead)
{
    assert(phead);//断言---头指针不能为空
    
    ListNode *cur = phead->next;//cur指向第一个节点（头节点的后一个节点）
    while(cur != phead)
    {
        printf("%d ",cur->data);//在遍历的同时将每一个值打印出来
        cur = cur->next;
    }
        
}

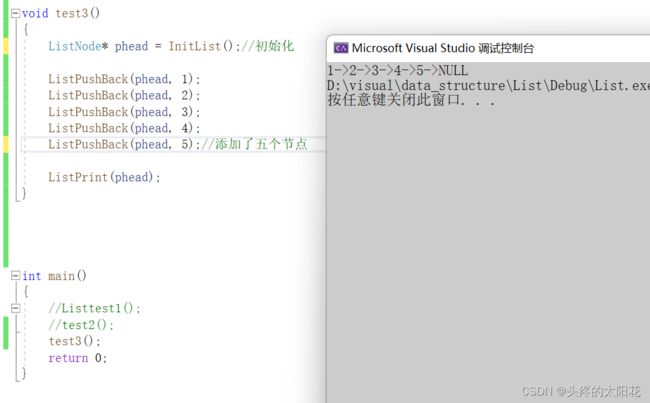
这里用一个事先创建好的链表，链表中有五个节点，一次存储的值为1，2，3，4，5；

打印的结果是：

查找链表中特定的节点

ListNode* ListFind(ListNode* phead, LTDataType x);
//返回值是一个我们需要找的节点的地址。

遍历整个链表，找到值为x的节点并且返回该节点的地址，找不到对应的节点就返回空指针

ListNode* ListFind(ListNode* phead, LTDataType x)
{
    assert(phead);
    
    ListNode *cur = phead->next;
    while(cur != phead)
    {
        if(cur->data == x)
        {
            return cur;
        }
        cur = cur->next;
    }
    return NULL;
}

一旦找到对应的节点，就可以返回该节点的地址，如果该节点不是我们需要找的节点，那么我们就判断下一个节点，一定要确定 了多有的节点都不满足要求才能返回空指针。

向链表中插入数据

向双向链表中插入数据比单向链表方便很多，因为双向链表中一个节点可以找到它前一个节点的地址，我们就不需要再用一个指针在遍历链表的时候专门保存前一个节点的地址了。

添加一个节点

我们要向链表中插入一个数据，就需要先得到一个节点，然后让这个节点和前后两个节点之间产生联系

ListNode* BuyListNode(LTDataType x)
{
	ListNode*newnode = (ListNode *)malloc(sizeof(ListNode));
	if (newnode == NULL)
	{
		printf("fail:malloc\n");
		return 0;
	}

	newnode->data = x;
	newnode->next = NULL;
	newnode->prev = NULL;

	return newnode;
}

创建新节点的时候，我们需要对这个节点赋值，然后再返回这个节点的地址。

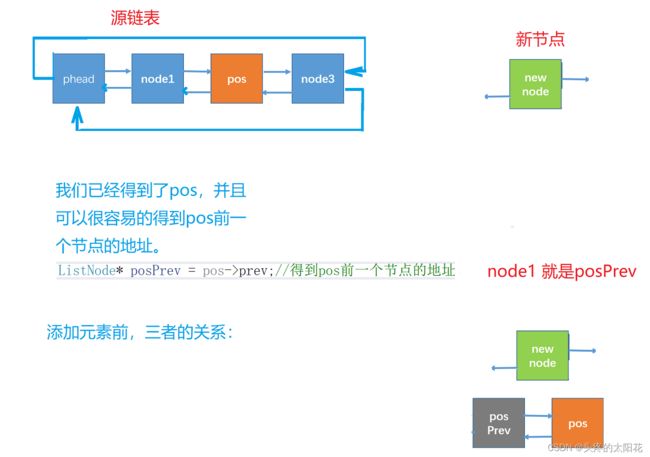
在指定位置前插入一个节点

我们在可以利用查找函数找到指定元素的位置，只要我们得到了这个位置，我们就可以在这个节点的前面插入元素

void ListInsert(ListNode *phead,ListNode* pos, LTDataType x);

由于我们可以通过这个位置直接找到前一个节点，所以我们可以不用遍历链表也能插入数据

//指定位置插入节点
void ListInsert(ListNode *phead,ListNode* pos, LTDataType x)
{
    assert(phead);
	assert(pos);//pos就是指定位置的节点

	ListNode* newnode = BuyListNode(x);//创建一个新的节点

	ListNode* posPrev = pos->prev;//得到指定节点的前一个节点
	
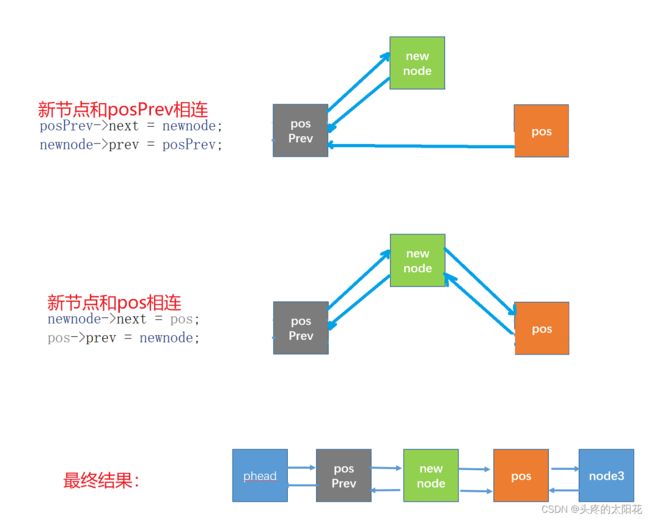
	posPrev->next = newnode;//新节点和前一个节点相连
	newnode->prev = posPrev;

	newnode->next = pos;//新节点和后一个节点相连
	pos->prev = newnode;
}

在链表尾插入一个节点

void ListPushBack(ListNode *phead);

在双向链表中，查找尾节点是不需要遍历链表的，最后一个节点就是哨兵位头指针的前一个节点,即phead->prev

void ListPushBack(ListNode* phead,LTDataType x)
{
	assert(phead);//断言头指针不为空

	ListNode* newnode = BuyNewNode(x);//创建一个值为x的节点
	
	//找到尾节点可以用phead->prev来表示尾节点的位置
	ListNode* tail = phead->prev;


	//和哨兵位节点相连
	phead->prev = newnode;
	newnode->next = phead;

	//和尾节点相连
	newnode->prev = tail;
	tail->next = newnode;

}

或者，我们可以利用前面已经完成的函数ListInsert,这个函数可以再任何一个位置插入节点，自然也包括了链表的头和尾。

不过我们需要注意参数的设置，再ListInsert函数中，我们是在指定节点的前一个位置插入节点，所以这里我们只需要将指定的位置设置为哨兵位的地址，因为哨兵位的前一个节点就是最后一个节点。

void ListPushBack(ListNode* phead,LTDataType x)
{
	assert(phead);
	ListInsert(phead,phead, x);
    //注意：
    //参数中两个phead表达的意思不同
    //这个函数的第一个参数phead表示的是指定的链表，第二个参数phead表示的是尾节点的后一个节点的地址。

}

在链表头插入一个节点

该链表的链表头就是哨兵位的下一个节点，我们每次可以直接将元素插入到哨兵位后面。

void ListPushFront(ListNode* phead,LTDataType x);

在链表头添加一个节点的意思就是在哨兵位节点和尾添加之前的第一个节点中间再添加一个节点。我们应该注意保存第一个节点的地址。

void ListPushFront(ListNode* phead, LTDataType x)
{
	assert(phead);

	ListNode* newnode = BuyListNode(x);

	ListNode *next = phead->next;//next就是未添加节点前的第一个节点。
    
	phead->next = newnode;
	newnode->prev = phead;//新节点和哨兵位相连

	next->prev = newnode;
	newnode->next = next;//新节点和next节点相连

}

同样我们可以利用ListInsert函数

void ListPushFront(ListNode* phead, LTDataType x)
{
	assert(phead);
	ListInsert(phead,phead->next, x);
}

注意：利用ListInsert头插元素的时候，我们是要将新节点插入到第二个参数的前面，也就是第一个节点的前面，第一个节点的地址是phead->next

删除链表中的数据

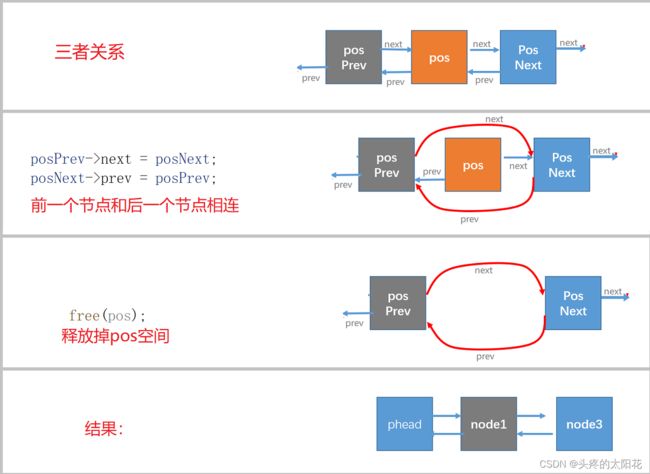
我们需要将指定位置的节点的前后两个节点相互连接，然后释放掉指定位置节点的空间。

删除指定位置的节点

我们可以通过查找函数找到指定的节点。

void ListErase(ListNode* phead,ListNode* pos);
//第一个参数指定了我们是操作的链表

注意：

再删除节点的时候，我们需要先判断该链表是否为空链表，如果这个连表示hi空链表，我们就不需要再删除，否则会出现非法访问的错误

非空链表的情况:
对于这样一个链表，我们已经得到了指定的节点位置

空链表的情况:

如果传过去的pos是哨兵位的地址，并且这是一个空该链表

在执行到最后free(pos)的时候，这个哨兵位就被删除了，后面如果还想要继续使用这个链表，就会出现访问错误

所以我们需要判断这个链表是否是空链表
可以利用判断语句，当判断出不为空链表的时候才执行删除操作。

void ListErase(ListNode* phead,ListNode* pos)
{
	assert(pos);
	assert(phead);//保证两个指针不是空指针


	if (phead->next != phead)//判断这个链表是不是空链表
	{
		ListNode* posPrev = pos->prev;//得到前一个节点的地址
		ListNode* posNext = pos->next;//得到后一个节点的地址

		posPrev->next = posNext;
		posNext->prev = posPrev;
		free(pos);
	}

}

删除链表的最后一个节点

函数的声明：

void ListPopBack(ListNode* phead);

删除链表的最后一个节点，就是让哨兵位和倒数第二个节点相连，然后释放掉最后一个节点的空间。

void ListPopBack(ListNode* phead)
{
	assert(phead);

	if (phead->next != phead)
	{
		ListNode* tail = phead->prev;//得到尾节点

		phead->prev = tail->prev;//头节点和倒数第二个节点相连
		tail->prev->next = phead;

		free(tail);//释放倒数第一个节点
	}


}

同样，我们可以利用前面写的ListErase函数

void ListPopBack(ListNode* phead)
{
	assert(phead);
    
	ListErase(phead,phead->prev);

}

注意：指定位置删除函数的第二个参数就直接是需要删除的节点的地址，所以当我们要删除最后一个节点的时候， 我们直接将最后一个节点的地址phead->prev作为参数即可。

删除链表的第一个节点

函数的声明：

void ListPopFront(ListNode* phead);

void ListPopFront(ListNode* phead)
{
	assert(phead);

	if (phead->next != phead)
	{
		ListNode *next = phead->next;//得到第一个节点的地址
        
		phead->next = next->next;//哨兵位和第二个节点相连
		next->next->prev = phead;
        
		free(next);//释放第一个节点

	}

	ListErase(phead,phead->next);
}

同样我们可以利用已经实现的函数

void ListPopFront(ListNode* phead)
{
	assert(phead);

	ListErase(phead,phead->next);
}

第一个节点的地址是phead->next，把第一个节点的地址传给指定位置删除函数就可以删除第一个节点了。

删除整个链表

删除整个链表同样需要遍历链表的操作----我们需要一次释放每一个节点的空间。

void ListDestroy(ListNode* phead)
{
	assert(phead);
	ListNode* cur = phead->next;
	while (cur->next != phead)
	{
		ListNode* next = cur->next;
		free(cur);
		cur = next;;
	}

}

由于这个链表的哨兵位节点也是动态分配出来的，所以我们也需要释放掉哨兵位的空间。

链表（带头双向循环）和顺序表

顺序表的优缺点

优点：

1. 物理空间是连续的，方便使用下标随机访问，很多排序算法是利用顺序表实现的。

2. 顺序表的CPU高速缓存命中率高。

高速缓存命中率:

假设我们有一个系统，它有一个CPU，一个寄存器文件，一个高速缓存和一个主存。

当CPU执行一条读内存字的指令的时候，它向高速缓存请求这个字，如果高速缓存中有这个字的副本，那么就称为高速缓存命中，CPU很快就可以从告诉缓存中得到这个字；如果高速缓存中没有这个字的副本，就称为高速缓存不命中，此时CPU就需要等待高速缓存从内存中读取这个字到缓存行后，再从告诉缓存中得到这个字

如果一个程序的高速缓存命中率高，那么这个程序的效率就高。

为什么说顺序表的告诉缓存命中率高呢？

因为顺序表中的数据物理地址是连续的，高速缓存每次从内存中读取数据的时候，不仅会读取需要的数据，还会将该数据后面的一部分数据也读取到缓存行中，这样下一次CPU向高速缓存读取数据的时候就很有很高概率命中。

​ 缺点：

1. 空间不够，需要扩容，扩容本身就有性能消耗，扩容机制还存在一定的空间浪费。

2. 插入、删除头部或者中部的数据效率低----时间复杂度为O(N)。

链表的优缺点

优点：

1. 可以按需申请、释放空间。
2. 任意位置节点的擦汗如删除效率高----时间复杂度为O(1)。

缺点：

1. 物理空间不连续，不支持下标的随机访问，有很多算法不支持，例如二分查找。

需要注意：两个数据结构各有各种的应用场景，不可能用一个结构万群代替另一个结构。

两个结构是相辅相成的，他们需要配合才能解决更多的问题。