用线性插值算法实现图像缩放
什么是双线性插值
简单比方
原来的数值序列:0,10,20,30,40
线性插值一次为:0,5,10,15,20,25,30,35,40
即认为其变化(增减)是线形的,可以在坐标图上画出一条直线
在数码相机技术中,这些数值可以代表组成一张照片的不同像素点的色彩、色度等指标。
为了方便理解,先考虑一维情况下的线性插值
对于一个数列c,我们假设c[a]到c[a+1]之间是线性变化的
那么对于浮点数x(a<=x<a+1),c(x)=c[a+1]*(x-a)+c[a]*(1+a-x);
这个好理解吧?
把这种插值方式扩展到二维情况
对于一个二维数组c,我们假设对于任意一个浮点数i,c(a,i)到c(a+1,i)之间是线性变化的,c(i,b)到c(i,b+1)之间也是线性变化的(a,b都是整数)
那么对于浮点数的坐标(x,y)满足(a<=x<a+1,b<=y<b+1),我们可以先分别求出c(x,b)和c(x,b+1):
c(x,b) = c[a+1]*(x-a)+c[a]*(1+a-x);
c(x,b+1) = c[a+1][b+1]*(x-a)+c[a][b+1]*(1+a-x);
好,现在已经知道c(x,b)和c(x,b+1)了,而根据假设c(x,b)到c(x,b+1)也是线性变化的,所以:
c(x,y) = c(x,b+1)*(y-b)+c(x,b)*(1+b-y)
这就是双线性插值
=====~~分割线桑~~=====~~分割线桑~~=====~~分割线桑~~=====
原理简述
在对图像进行空间变换的过程中,典型的情况是在对图像进行放大处理的时候,图像会出现失真的现象。这是由于在变换之后的图像中,存在着一些变换之前的图像中没有的像素位置。为了说明这个问题,不妨假设有一副大小为64x64的灰度图像A,现在将图像放大到256x256,不妨令其为图像B,如图 1所示。显然,根据简单的几何换算关系,可以知道B图像中(x,y)处的像素值应该对应着A图像中的(x/4,y/4)处的象素值,即
B(x,y) = A(x/4,y/4) (式1)
对于B中的(4,4),(4,8),(4,16)…(256,256)这些位置,通过式1就可以计算出其在A中的位置,从而可以得到灰度值。但是,对于B中的(1,1),(1,2),(1,3)…等等这些坐标点而言,如果按照式1计算的话,那么它们在A中对应的坐标不再是整数。比如,对于B中的坐标点(1,1),其在A中的对应坐标就变成了(0.25,0.25)。对于数字图像而言,小数坐标是没有意义的。因此,必须考虑采用某种方法来得到B中像素点在A中对应位置上的灰度级。
处理这一问题的方法被称为图像灰度级插值。常用的插值方式有三种:最近邻域插值、双线性插值、双三次插值。理论上来讲,最近邻域插值的效果最差,双三次插值的效果最好,双线性插值的效果介于两者之间。不过对于要求不是非常严格的图像插值而言,使用双线性插值通常就足够了。
本文中将采用matlab实现一个双线性插值的程序。
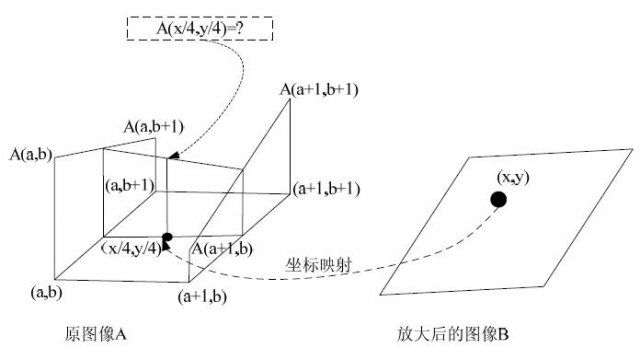
双线性插值的原理如图 2所示。图像之间坐标映射有两种方式:如果是从原图像的坐标映射到目标图像,称为前向映射,反之则称为后向映射。显然,双线性插值采用的是后向映射方式。
下面对图 2的具体含义进行说明。首先,根据几何关系,从B图像中的坐标(x,y)得到A图像中的坐标(x/4,y/4),但是,映射得到的这个坐标(x/4,y/4)并没有刚好位于A图像中的整数坐标上,而是映射到了四个像素坐标(a,b)、(a+1,b)、(a,b+1)、(a+1,b+1)所围成的矩形之间,其中,a、b是A图像的整数坐标。现在的问题就是如何根据A(a,b)、A(a+1,b)、A(a,b+1)、A(a+1,b+1)这四个点上的灰度级求出A(x/4,y/4)处的灰度级。双线性插值技术采用的方法是:假设A图像的灰度级变化在纵向方向上是线性变化的,这样根据直线方程或者几何比例关系就能够求得(a,y/4)和(a+1,y/4)坐标处的灰度级A(a,y/4)和A(a+1,y/4)。然后,再假设在((a,y/4),A(a,y/4))和(a+1,y/4),A(a+1,y/4))这两点所确定的直线上,灰度级仍然是线性变化的。求出直线方程,于是就可以求得(x/4,y/4)处的灰度级A(x/4,y/4)。这就是双线性插值的基本思路。其中用到的两个基本假设是:首先灰度级在纵向方向上是线性变化的,然后假定灰度级在横向方向上也是线性变化的。
=====~~分割线桑~~=====~~分割线桑~~=====~~分割线桑~~=====
在 Windows 中做过图像方面程序的人应该都知道 Windows 的 GDI 有一个 API 函数: StretchBlt ,对应在 VCL 中是 TCanvas 类的 StretchDraw 方法。它可以很简单地实现图像的缩放操作。但问题是它是用了速度最快,最简单但效果也是最差的“最近邻域法”,虽然在大多数情况下,它也够用了,但对于要求较高的情况就不行了。
不久前我做了一个小玩意儿(见 《人个信息助理之我的相册》 ),用于管理我用 DC 拍的一堆照片,其中有一个插件提供了缩放功能,目前的版本就是用了 StretchDraw ,有时效果不能令人满意,我一直想加入两个更好的:线性插值法和三次样条法。经过研究发现三次样条法的计算量实在太大,不太实用,所以决定就只做线性插值法的版本了。
从数字图像处理的基本理论,我们可以知道:图像的变形变换就是源图像到目标图像的坐标变换。简单的想法就是把源图像的每个点坐标通过变形运算转为目标图像的相应点的新坐标,但是这样会导致一个问题就是目标点的坐标通常不会是整数,而且像放大操作会导致目标图像中没有被源图像的点映射到,这是所谓“向前映射” 方法的缺点。所以一般都是采用“逆向映射”法。
但是逆向映射法同样会出现映射到源图像坐标时不是整数的问题。这里就需要“重采样滤波器”。这个术语看起来很专业,其实不过是因为它借用了电子信号处理中的惯用说法(在大多数情况下,它的功能类似于电子信号处理中的带通滤波器),理解起来也不复杂,就是如何确定这个非整数坐标处的点应该是什么颜色的问题。前面说到的三种方法:最近邻域法,线性插值法和三次样条法都是所谓的“重采样滤波器”。
所谓“最近邻域法”就是把这个非整数坐标作一个四舍五入,取最近的整数点坐标处的点的颜色。而“线性插值法”就是根据周围最接近的几个点(对于平面图像来说,共有四点)的颜色作线性插值计算(对于平面图像来说就是二维线性插值)来估计这点的颜色,在大多数情况下,它的准确度要高于最近邻域法,当然效果也要好得多,最明显的就是在放大时,图像边缘的锯齿比最近邻域法小非常多。当然它同时还带业个问题:就是图像会显得比较柔和。这个滤波器用专业术语来说(呵呵,卖弄一下偶的专业 ^_^ )叫做:带阻性能好,但有带通损失,通带曲线的矩形系数不高。至于三次样条法我就不说了,复杂了一点,可自行参考数字图像处理方面的专业书籍,如本文的参考文献。
再来讨论一下坐标变换的算法。简单的空间变换可以用一个变换矩阵来表示:
[x’,y’,w’]=[u,v,w]*T
其中: x’,y’ 为目标图像坐标, u,v 为源图像坐标, w,w’ 称为齐次坐标,通常设为 1 , T 为一个 3X3 的变换矩阵。
这种表示方法虽然很数学化,但是用这种形式可以很方便地表示多种不同的变换,如平移,旋转,缩放等。对于缩放来说,相当于:
[Su 0 0 ]
[x, y, 1] = [u, v, 1] * [0 Sv 0 ]
[0 0 1 ]
其中 Su,Sv 分别是 X 轴方向和 Y 轴方向上的缩放率,大于 1 时放大,大于 0 小于 1 时缩小,小于 0 时反转。
矩阵是不是看上去比较晕?其实把上式按矩阵乘法展开就是:
{ x = u * Su
{ y = v * Sv
就这么简单。 ^_^
有了上面三个方面的准备,就可以开始编写代码实现了。思路很简单:首先用两重循环遍历目标图像的每个点坐标,通过上面的变换式(注意:因为是用逆向映射,相应的变换式应该是: u = x / Su 和 v = y / Sv )取得源坐标。因为源坐标不是整数坐标,需要进行二维线性插值运算:
P = n*b*PA + n * ( 1 – b )*PB + ( 1 – n ) * b * PC + ( 1 – n ) * ( 1 – b ) * PD
其中: n 为 v (映射后相应点在源图像中的 Y 轴坐标,一般不是整数)下面最接近的行的 Y 轴坐标与 v 的差;同样 b 也类似,不过它是 X 轴坐标。 PA-PD 分别是 (u,v) 点周围最接近的四个(左上,右上,左下,右下)源图像点的颜色(用 TCanvas 的 Pixels 属性)。 P 为 (u,v) 点的插值颜色,即 (x,y) 点的近似颜色。
这段代码我就不写的,因为它的效率实在太低:要对目标图像的每一个点的 RGB 进行上面那一串复杂的浮点运算。所以一定要进行优化。对于 VCL 应用来说,有个比较简单的优化方法就是用 TBitmap 的 ScanLine 属性,按行进行处理,可以避免 Pixels 的像素级操作,对性能可以有很大的改善。这已经是算是用 VCL 进行图像处理的基本优化常识了。不过这个方法并不总是管用的,比如作图像旋转的时候,这时需要更多的技巧。
无论如何,浮点运算的开销都是比整数大很多的,这个也是一定要优化掉的。从上面可以看出,浮点数是在变换时引入的,而变换参数 Su,Sv 通常就是浮点数,所以就从它下手优化。一般来说, Su,Sv 可以表示成分数的形式:
Su = ( double )Dw / Sw; Sv = ( double )Dh / Sh
其中 Dw, Dh 为目标图像的宽度和高度, Sw, Sh 为源图像的宽度和高度(因为都是整数,为求得浮点结果,需要进行类型转换)。
将新的 Su, Sv 代入前面的变换公式和插值公式,可以导出新的插值公式:
因为:
b = 1 – x * Sw % Dw / ( double )Dw; n = 1 – y * Sh % Dh / ( double )Dh
设:
B = Dw – x * Sw % Dw; N = Dh – y * Sh % Dh
则:
b = B / ( double )Dw; n = N / ( double )Dh
用整数的 B , N 代替浮点的 b, n ,转换插值公式:
P = ( B * N * ( PA – PB – PC + PD ) + Dw * N * PB + DH * B * PC + ( Dw * Dh – Dh * B – Dw * N ) * PD ) / ( double )( Dw * Dh )
这里最终结果 P 是浮点数,对其四舍五入即可得到结果。为完全消除浮点数,可以用这样的方法进行四舍五入:
P = ( B * N … * PD + Dw * Dh / 2 ) / ( Dw * Dh )
这样, P 就直接是四舍五入后的整数值,全部的计算都是整数运算了。
简单优化后的代码如下:
int __fastcall TResizeDlg::Stretch_Linear(Graphics::TBitmap * aDest, Graphics::TBitmap * aSrc)
{
int sw = aSrc->Width - 1, sh = aSrc->Height - 1, dw = aDest->Width - 1, dh = aDest->Height - 1;
int B, N, x, y;
int nPixelSize = GetPixelSize( aDest->PixelFormat );
BYTE * pLinePrev, *pLineNext;
BYTE * pDest;
BYTE * pA, *pB, *pC, *pD;
for ( int i = 0; i <= dh; ++i )
{
pDest = ( BYTE * )aDest->ScanLine[i];
y = i * sh / dh;
N = dh - i * sh % dh;
pLinePrev = ( BYTE * )aSrc->ScanLine[y++];
pLineNext = ( N == dh ) ? pLinePrev : ( BYTE * )aSrc->ScanLine[y];
for ( int j = 0; j <= dw; ++j )
{
x = j * sw / dw * nPixelSize;
B = dw - j * sw % dw;
pA = pLinePrev + x;
pB = pA + nPixelSize;
pC = pLineNext + x;
pD = pC + nPixelSize;
if ( B == dw )
{
pB = pA;
pD = pC;
}
for ( int k = 0; k < nPixelSize; ++k )
*pDest++ = ( BYTE )( int )(
( B * N * ( *pA++ - *pB - *pC + *pD ) + dw * N * *pB++
+ dh * B * *pC++ + ( dw * dh - dh * B - dw * N ) * *pD++
+ dw * dh / 2 ) / ( dw * dh )
);
}
}
return 0;
}
应该说还是比较简洁的。因为宽度高度都是从 0 开始算,所以要减一, GetPixelSize 是根据 PixelFormat 属性来判断每个像素有多少字节,此代码只支持 24 或 32 位色的情况(对于 15 或 16 位色需要按位拆开 — 因为不拆开的话会在计算中出现不期望的进位或借位,导致图像颜色混乱 — 处理较麻烦;对于 8 位及 8 位以下索引色需要查调色板,并且需要重索引,也很麻烦,所以都不支持;但 8 位灰度图像可以支持)。另外代码中加入一些在图像边缘时防止访问越界的代码。
通过比较,在 PIII-733 的机器上,目标图像小于 1024x768 的情况下,基本感觉不出速度比 StretchDraw 有明显的慢(用浮点时感觉比较明显)。效果也相当令人满意,不论是缩小还是放大,图像质量比 StretchDraw 方法有明显提高。
不过由于采用了整数运算,有一个问题必须加以重视,那就是溢出的问题:由于式中的分母是 dw * dh ,而结果应该是一个 Byte 即 8 位二进制数,有符号整数最大可表示 31 位二进制数,所以 dw * dh 的值不能超过 23 位二进制数,即按 2:1 的宽高比计算目标图像分辨率不能超过 4096*2048 。当然这个也是可以通过用无符号数(可以增加一位)及降低计算精度等方法来实现扩展的,有兴趣的朋友可以自己试试。
当然这段代码还远没有优化到极致,而且还有很多问题没有深入研究,比如抗混叠( anti-aliasing )等,有兴趣的朋友可以自行参考相关书籍研究,如果你有什么研究成果,非常欢迎你为我的程序编写插件实现。
[ Mental Studio ] 猛禽
2004-3-28
参考文献:
崔屹《数字图像处理技术与应用》电子工业出版社, 1997
//上面的只能是24位的位图,现在修改了以个Delphi版本的,支持多种位图格式了,应该。测试,32和24位都可
procedure StretchBitmap(Dest, Src: TBitmap);
var
sw, sh, dw, dh, B, N, x, y, i, j, k, nPixelSize: DWord;
pLinePrev, pLineNext, pDest, pA, pB, pC, pD: PByte;
begin
sw := Src.Width -1;
sh := Src.Height -1;
dw := Dest.Width -1;
dh := Dest.Height -1;
//获得显示模式
nPixelSize := Integer(Src.PixelFormat);
if nPixelSize < 4 then
nPixelSize := 4
else if nPixelSize = 4 then
inc(nPixelSize)
else if nPixelSize > 7 then
nPixelSize := 7;
Dest.PixelFormat := TPixelFormat(nPixelSize);
nPixelSize := nPixelSize - 3;
for i := 0 to dh do
begin
pDest := Dest.ScanLine[i];
y := i * sh div dh;
N := dh - i * sh mod dh;
pLinePrev := Src.ScanLine[y];
Inc(y);
if N = dh then
pLineNext := pLinePrev
else
pLineNext := Src.ScanLine[y];
for j := 0 to dw do
begin
x := j * sw div dw * nPixelSize;
B := dw - j * sw mod dw;
pA := pLinePrev;
Inc(pA, x);
pB := pA;
Inc(pB, nPixelSize);
pC := pLineNext;
Inc(pC, x);
pD := pC;
Inc(pD, nPixelSize);
if B = dw then begin
pB := pA;
pD := pC;
end;
for k := 0 to nPixelSize -1 do
begin
pDest^ := Byte(DWord( (B * N * DWord(pA^ - pB^ - pC^ + pD^) + dw * N * pB^
+ dh * B * pC^ + (dw * dh - dh * B - dw * N)* pD^
+ dw * dh div 2) div (dw * dh) ));
Inc(pDest);
Inc(pA);
Inc(pB);
Inc(pC);
Inc(pD);
end;
end;
end;
end;