《菜菜的机器学习sklearn课堂，细谈分布式事务的前世今生

簇中所有数据的均值 μ \mu μ通常被称为这个簇的质心(centroids)。在一个二维平面中，一簇数据点的质心的横坐标就是这一簇数据点的横坐标的均值，质心的纵坐标就是这一簇数据点的纵坐标的均值。同理可推广至高维空间。

---

在KMeans算法中，簇的个数K是一个超参数，需要我们人为输入来确定。KMeans的核心任务就是根据我们设定好的K，找出K个最优的质心，并将离这些质心最近的数据分别分配到这些质心代表的簇中去。具体过程可以总结如下：

| 顺序 | 过程 |

| — | — |

| 1 | 随机抽取K个样本作为最初的质心 |

| 2 | 开始循环： |

| 2.1 | 将每个样本点分配到离他们最近的质心，生成K个簇 |

| 2.2 | 对于每个簇，计算所有被分到该簇的样本点的平均值作为新的质心 |

| 3 | 当质心的位置不再发生变化，迭代停止，聚类完成 |

什么情况下，质心的位置会不再变化呢？

• 当我们找到一个质心，在每次迭代中被分配到这个质心上的样本都是一致的，即每次新生成的簇都是一致的，所有的样本点都不会再从一个簇转移到另一个簇，质心就不会变化了。

这个过程在可以由下图来显示，我们规定将数据分为4(K=4)，其中白色X代表质心的位置：

可以看见，第六次迭代之后，基本上质心的位置就不再改变了，生成的簇也变得稳定。此时我们的聚类就完成了，我们可以明显看出，KMeans按照数据的分布，将数据聚集成了我们规定的4类，接下来我们就可以按照我们的业务需求或者算法需求，对这四类数据进行不同的处理。

[](

)簇内误差平方和的定义和解惑

---

聚类算法聚出的类有什么含义呢？这些类有什么样的性质？

我们认为，被分在同一个簇中的数据是有相似性的，而不同簇中的数据是不同的，当聚类完毕之后，我们就要分别去研究每个簇中的样本都有什么样的性质，从而根据业务需求制定不同的商业或者科技策略。

这个听上去和评分卡案例中讲解的“分箱”概念有些类似，即我们分箱的目的是希望：一个箱内的人有着相似的信用风险，而不同箱的人的信用风险差异巨大，以此来区别不同信用度的人，因此我们追求“组内差异小，组间差异大”。

聚类算法也是同样的目的，我们追求“簇内差异小，簇外差异大”。而这个“差异“，由样本点到其所在簇的质心的距离来衡量。

对于一个簇来说，所有样本点到质心的距离之和越小，我们就认为这个簇中的样本越相似，簇内差异就越小。而距离的衡量方法有多种，

• 令 x x x表示簇中的一个样本点

• μ \mu μ表示该簇中的质心

• n表示每个样本点中的特征数目

• i表示组成点 x x x的每个特征

则该样本点到质心的距离可以由以下距离来度量：

• 欧几里得距离 ： d ( x , μ ) = ∑ i = 1 n ( x i − x μ ) 2 d(x, \mu) = \sqrt{\sum_{i=1} ^n (x_i - x_\mu)^2} d(x,μ)=i=1∑n​(xi​−xμ​)2 ​

• 曼哈顿距离： d ( x , μ ) = ∑ i = 1 n ( ∣ x i − μ ∣ ) d(x, \mu) = \sum_{i=1}^{n}(|x_i - \mu|) d(x,μ)=i=1∑n​(∣xi​−μ∣)

• 余弦距离： c o s θ = ∑ 1 n ( x i ∗ μ ) ∑ 1 n ( x i ) 2 ∗ ∑ 1 n ( μ ) 2 cos\theta = \frac { \sum _1^n(x_i * \mu)} {\sqrt {\sum_1^n(x_i)2} * \sqrt{\sum_1^n(\mu)2}} cosθ=∑1n​(xi​)2 ​∗∑1n​(μ)2 ​∑1n​(xi​∗μ)​

如我们采用欧几里得距离，则一个簇中所有样本点到质心的距离的平方和为：

其中，m为一个簇中样本的个数，j是每个样本的编号。

这个公式被称为簇内平方和(cluster Sum of Square)，又叫做Inertia。而将一个数据集中的所有簇的簇内平方和相加，就得到了整体平方和(Total Cluster Sum ofSquare)，又叫做total inertia。Total Inertia越小，代表着每个簇内样本越相似，聚类的效果就越好。因此KMeans追求的是：求解能够让Inertia最小化的质心。

实际上，在质心不断变化不断迭代的过程中，总体平方和是越来越小的。我们可以使用数学来证明，当整体平方和最小的时候，质心就不再发生变化了。如此，K-Means的求解过程，就变成了一个最优化问题。

这是我们第二次遇见最优化问题，即需要将某个指标最小化来求解模型中的一部分信息。

记得我们在逻辑回归中式怎么做的吗：我们在一个固定的方程 y ( x ) = 1 e θ T x y(x) = \frac 1 {e^{\thetaTx}} y(x)=eθTx1​中最小化损失函数来求解模型的参数向量 θ \theta θ，并且基于参数向量 θ \theta θ的存在去使用模型。

在KMeans中，我们在一个固定的簇数K下，最小化总体平方和来求解最佳质心，并基于质心的存在去进行聚类。两个过程十分相似，并且，整体距离平方和的最小值其实可以使用梯度下降来求解。因此，有许多博客和教材都这样写道：“簇内平方和/整体平方和是KMeans的损失函数”。

解惑：Kmeans有损失函数吗？

损失函数本质是用来衡量模型的拟合效果的，只有有着求解参数需求的算法，才会有损失函数。

Kmeans不求解什么参数，它的模型本质也没有在拟合数据，而是在对数据进行一种探索。所以如果你去问大多数数据挖掘工程师，甚至是算法工程师，他们可能会告诉你说，K-Means不存在什么损失函数，Inertia更像是Kmeans的模型评估指标，而非损失函数。

但我们类比过了Kmeans中的Inertia和逻辑回归中的损失函数的功能，发现它们确实非常相似。所以，从“求解模型中的某种信息，用于后续模型的使用“这样的功能来看，我们可以认为Inertia是Kmeans中的损失函数，虽然这种说法并不严谨。

对比来看，在决策树中，我们有衡量分类效果的指标准确度accuracy，准确度所对应的损失叫做泛化误差，但我们不能通过最小化泛化误差来求解某个模型中需要的信息，我们只是希望模型的效果上表现出来的泛化误差很小。因此决策树，KNN等算法，是绝对没有损失函数的。

大家可以发现，我们的Inertia是基于欧几里得距离的计算公式得来的。实际上，我们也可以使用其他距离，每个距离都有自己对应的Inertia。在过去的经验中，我们总结出不同距离所对应的质心选择方法和Inertia，在Kmeans中，只要使用了正确的质心和距离组合，无论使用什么样的距离，都可以达到不错的聚类效果：

这些组合，都可以由严格的数学证明来推导。在sklearn当中，我们无法选择使用的距离，只能使用欧式距离。因此，我们也无需去担忧这些距离所搭配的质心选择是如何得来的了。

[](

)sklearn.cluster.KMeans

=========================================================================================

class sklearn.cluster.KMeans (

	n_clusters=8, 

	init=’k-means++’, 

	n_init=10, 

	max_iter=300, 

	tol=0.0001,

	precompute_distances=’auto’, 

	verbose=0, 

	random_state=None,

 	copy_x=True, 

 	n_jobs=None,

 	algorithm=’auto’

) 

[](

)重要参数 n_clusters

---

n_clusters 是 KMeans 中的 k，表示着我们告诉模型我们要分几类

• 这是KMeans当中唯一一个必填的参数，默认为8类，但通常我们的聚类结果会小于8

• 开始聚类之前，我们通常并不知道n_clusters究竟是多少，因此我们要对它进行探索

[](

)【实践】尝试聚类一次

---

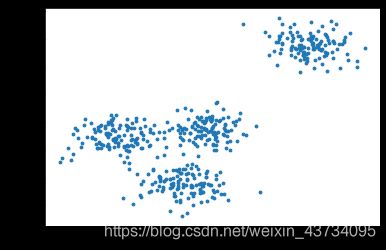
当我们拿到一个数据集，如果可能的话，我们希望能够通过绘图先观察一下这个数据集的数据分布，以此来为我们聚类时输入的n_clusters做一个参考。

首先，我们来自己创建一个数据集。这样的数据集是我们自己创建，所以是有标签的。

from sklearn.datasets import make_blobs

import matplotlib.pyplot as plt



#自己创建数据集

X, y = make_blobs(n_samples=500,n_features=2,centers=4,random_state=1)

fig, ax1 = plt.subplots(1)

ax1.scatter(X[:, 0], X[:, 1]

           ,marker='o' #点的形状

           ,s=8 #点的大小

           )

plt.show() 

基于这个分布，我们来使用Kmeans进行聚类。首先，我们要猜测一下，这个数据中有几簇？

• 根据上面画出的图，我们先猜测有 3 簇

from sklearn.cluster import KMeans

n_clusters = 3

cluster = KMeans(n_clusters=n_clusters, random_state=0).fit(X)



y_pred = cluster.labels_ #标签类别

y_pred



pre = cluster.fit_predict(X)

pre == y_pred



cluster_smallsub = KMeans(n_clusters=n_clusters, random_state=0).fit(X[:200])

y_pred_ = cluster_smallsub.predict(X)

y_pred == y_pred_



centroid = cluster.cluster_centers_ # 质心

centroid

"""

array([[-8.09286791, -3.50997357],

       [-1.54234022,  4.43517599],

       [-7.0877462 , -8.08923534]])

"""



centroid.shape

"""

(3, 2)

"""



inertia = cluster.inertia_ #簇内平方和

inertia

"""

1903.5342237665059

""" 

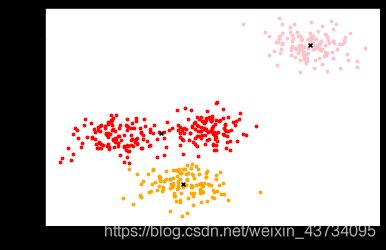
画出 n_clusters = 3 时的聚类图：

color = ["red","pink","orange","gray"]

fig, ax1 = plt.subplots(1)

for i in range(n_clusters):

    ax1.scatter(X[y_pred==i, 0], X[y_pred==i, 1]

           ,marker='o'

           ,s=8

           ,c=color[i]

           )

ax1.scatter(centroid[:,0],centroid[:,1]

           ,marker="x"

           ,s=15

           ,c="black")

plt.show() 

调整 n_clusters 的值，查看对应的簇内平方和：

• 发现当 n_clusters 越大，簇内平方和越小，这能说明聚类效果好吗？（并不能）

n_clusters = 4

cluster_ = KMeans(n_clusters=n_clusters, random_state=0).fit(X)

inertia_ = cluster_.inertia_

inertia_

"""

908.3855684760603

"""



n_clusters = 5

cluster_ = KMeans(n_clusters=n_clusters, random_state=0).fit(X)

inertia_ = cluster_.inertia_

inertia_

"""

811.0952123653016

"""



n_clusters = 6

cluster_ = KMeans(n_clusters=n_clusters, random_state=0).fit(X)

inertia_ = cluster_.inertia_

inertia_

"""

728.2827697678249z

""" 

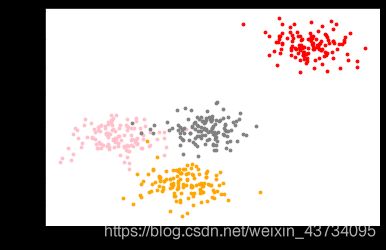
查看点的实际分布

color = ["red","pink","orange","gray"]

fig, ax1 = plt.subplots(1)

for i in range(4):

    ax1.scatter(X[y==i, 0], X[y==i, 1]

           ,marker='o' #点的形状

           ,s=8 #点的大小

           ,c=color[i]

           )

plt.show() 

[](

)聚类算法的模型评估指标

---

不同于分类模型和回归，聚类算法的模型评估不是一件简单的事。

在分类中，有直接结果（标签）的输出，并且分类的结果有正误之分，所以我们使用预测的准确度，混淆矩阵，ROC曲线等等指标来进行评估，但无论如何评估，都是在”模型找到正确答案“的能力。

而回归中，由于要拟合数据，我们有SSE均方误差，有损失函数来衡量模型的拟合程度。

但这些衡量指标都不能够使用于聚类。

面试高频问题：如何衡量聚类算法的效果？

聚类模型的结果不是某种标签输出，并且聚类的结果是不确定的，其优劣由业务需求或者算法需求来决定，并且没有永远的正确答案。那我们如何衡量聚类的效果呢？

记得我们说过，KMeans的目标是确保“簇内差异小，簇外差异大”，我们就可以通过衡量簇内差异来衡量聚类的效果。而Inertia是用距离来衡量簇内差异的指标，因此，我们是否可以使用Inertia来作为聚类的衡量指标呢？Inertia越小模型越好嘛?

可以，但是这个指标的缺点和极限太大。

• 首先，它不是有界的。我们只知道，Inertia是越小越好，是0最好，但我们不知道，一个较小的Inertia究竟有没有达到模型的极限，能否继续提高。

• 第二，它的计算太容易受到特征数目的影响，数据维度很大的时候，Inertia的计算量会陷入维度诅咒之中，计算量会爆炸，不适合用来一次次评估模型。

• 第三，它会受到超参数K的影响，在我们之前的尝试中其实我们已经发现，随着K越大，Inertia注定会越来越小，但这并不代表模型的效果越来越好了

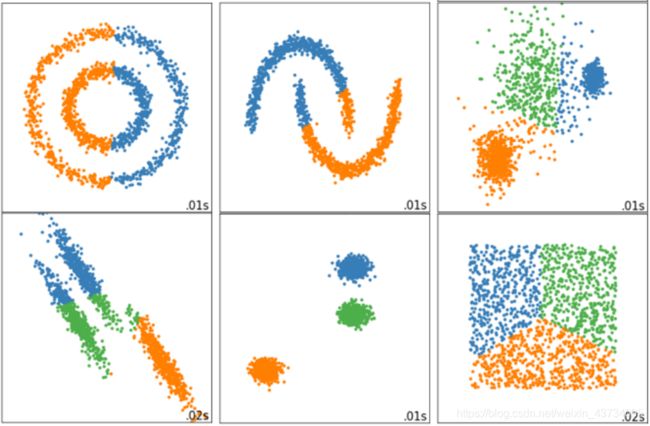
• 第四，Inertia对数据的分布有假设，它假设数据满足凸分布（即数据在二维平面图像上看起来是一个凸函数的样子），并且它假设数据是各向同性的（isotropic），即是说数据的属性在不同方向上代表着相同的含义。但是现实中的数据往往不是这样。所以使用Inertia作为评估指标，会让聚类算法在一些细长簇，环形簇，或者不规则形状的流形时表现不佳：

  

那我们可以使用什么指标呢？分两种情况来看。

• 真实标签已知的时候

• 真实标签未知的时候

[](

)当真实标签已知的时候

虽然我们在聚类中不输入真实标签，但这不代表我们拥有的数据中一定不具有真实标签，或者一定没有任何参考信息。当然，在现实中，拥有真实标签的情况非常少见（几乎是不可能的）。如果拥有真实标签，我们更倾向于使用分类算法。但不排除我们依然可能使用聚类算法的可能性。如果我们有样本真实聚类情况的数据，我们可以对于聚类算法的结果和真实结果来衡量聚类的效果。常用的有以下三种方法：

[](

)当真实标签未知的时候：轮廓系数

最后，附一张自己面试前准备的脑图：

面试前一定少不了刷题，为了方便大家复习，我分享一波个人整理的面试大全宝典

• Java核心知识整理

• Spring全家桶（实战系列）

Step3：刷题

既然是要面试，那么就少不了刷题，实际上春节回家后，哪儿也去不了，我自己是刷了不少面试题的，所以在面试过程中才能够做到心中有数，基本上会清楚面试过程中会问到哪些知识点，高频题又有哪些，所以刷题是面试前期准备过程中非常重要的一点。

以下是我私藏的面试题库：

很多人感叹“学习无用”，实际上之所以产生无用论，是因为自己想要的与自己所学的匹配不上，这也就意味着自己学得远远不够。无论是学习还是工作，都应该有主动性，所以如果拥有大厂梦，那么就要自己努力去实现它。

**[CodeChina开源项目：【一线大厂Java面试题解析+核心总结学习笔记+最新讲解视频】](

)**

片转存中…(img-VsHRLwBS-1631189925642)]

面试前一定少不了刷题，为了方便大家复习，我分享一波个人整理的面试大全宝典

• Java核心知识整理

[外链图片转存中…(img-TCNUrDBR-1631189925644)]

• Spring全家桶（实战系列）

[外链图片转存中…(img-ylPKnd8z-1631189925646)]

Step3：刷题

既然是要面试，那么就少不了刷题，实际上春节回家后，哪儿也去不了，我自己是刷了不少面试题的，所以在面试过程中才能够做到心中有数，基本上会清楚面试过程中会问到哪些知识点，高频题又有哪些，所以刷题是面试前期准备过程中非常重要的一点。

以下是我私藏的面试题库：

[外链图片转存中…(img-CZuuTg0W-1631189925647)]

很多人感叹“学习无用”，实际上之所以产生无用论，是因为自己想要的与自己所学的匹配不上，这也就意味着自己学得远远不够。无论是学习还是工作，都应该有主动性，所以如果拥有大厂梦，那么就要自己努力去实现它。

**[CodeChina开源项目：【一线大厂Java面试题解析+核心总结学习笔记+最新讲解视频】](

)**

最后祝愿各位身体健康，顺利拿到心仪的offer！