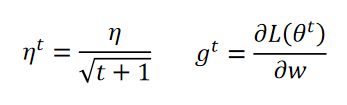机器学习笔记 Gradient Descent--递归下降
Gradient Descent
Review
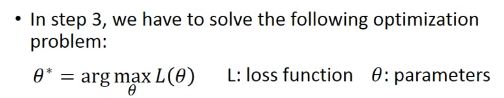
在第三步,我们得通过调整参数θ去使损失函数达的结果达到最小,既找到评分最高的function的参数θ。

我们通过η学习率(调整的幅度)和偏导(调整的方向)去调整参数θ。
调整的过程就是Gradient Descent
在θ处的Gradient为:

【梯度代表上升最快的方向,所以我们要减去梯度,既往下降最快的方向走】
进一步把方程写成:

Learning Rate的影响
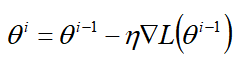
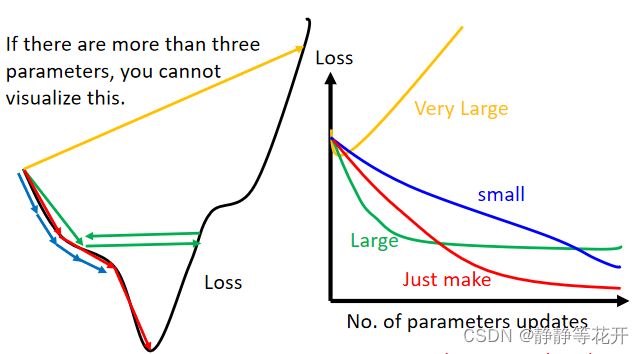
下图左图,
(1)当Learning Rate设置的很小时,Loss下降的速度会很慢;
(2)当Learning Rate比较大时,第一次Loss下降的比较快,然后就在“山谷”来回震荡,下降速度变缓慢;
(3)当Learning Rate设置的很大时,Loss直接飞了出去,急剧变大。
Conclusion:所以我们应该小心的选择Learning Rate。
Adaptive Learning Rates调整Learning Rates
比较流行也比较简单的方法是:在每一轮的参数调整后减少学习率。
(1)在刚开始,我们可以选择较大的学习率。因为我们离“山谷”会比较远。
(2)在几轮结束后,我们可以选择减小学习率。因为我们离“山谷”比较近。
【但该公式不可能适合所有的参数调整过程,也许我们可以为不同的参数调整设置不同的学习率】
Adagrad自适应梯度算法
对每个参数设置不同的学习率方程
(2)Adagrad自适应梯度算法

σ为历史偏导平方和的平均值再开根号
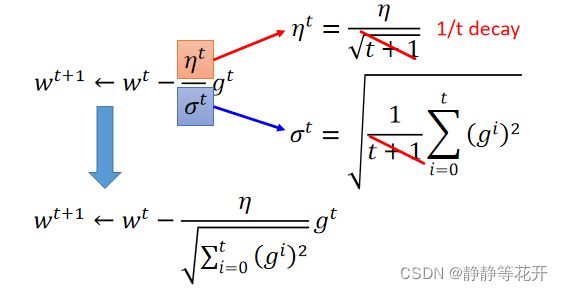
【个人理解,首先σ是逐渐增大的,保证了学习率会逐渐减小;当偏导很大时,表示下降幅度比较大,“山谷”可能会比较窄,所有学习率减小的应该多一些,所有σ会比较大,从而学习率减少的比较大】
Best Step?每次跨多大步伐是最好的?
取一个二次方程为例子
 上图上部分是function的图像,下部分是function一阶导数图像。
上图上部分是function的图像,下部分是function一阶导数图像。
可以看出x0点到达局部最优点的Best step为|x0+b/(2a)|。可化简为:
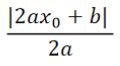
所以Best step与 2ax0+b 成正比,而2ax0+b正好是该函数的一阶导数,所以Best step和一阶导成正比。
但这结论不能跨越参数,既对于每个参数都有自己的Best step距离。
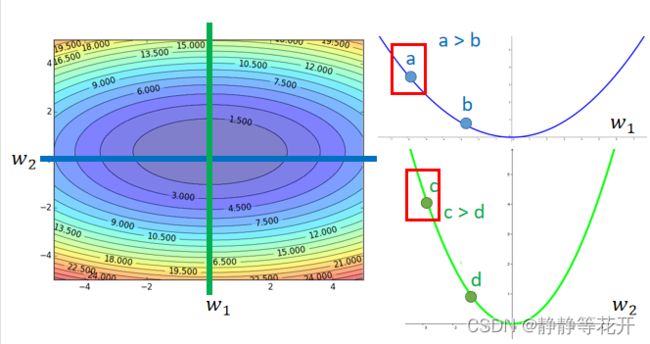 如上图,对于两个不同的参数,他们对于的Loss曲线是不同的,对于的一阶导也存在差异,一个Best step不能同时反应w1和w2距离最佳点的距离。
如上图,对于两个不同的参数,他们对于的Loss曲线是不同的,对于的一阶导也存在差异,一个Best step不能同时反应w1和w2距离最佳点的距离。
我们在观察一下上述Best step 的分母,
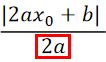
可以发现分子其实就是function的二次导数。所以Best step和二次导数成反比
【我的理解:二次导数代表凹凸性,所以当二次导数很大时,代表函数比较尖,或者说山谷比较窄,Best step就应该比较小】

conclusion:Best step应该正比于一阶导,反比于二阶导
那Adagrad中的分母是二阶导,分子是一阶导吗?
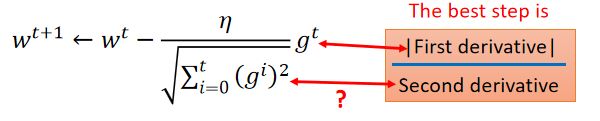
(1)首先η是学习率,可以看作一个常数。
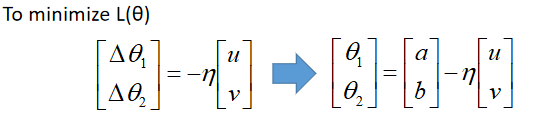
(2)而gt代表梯度,本身就是一阶导;
(3)分母就是使用一阶导数取估值二阶导数
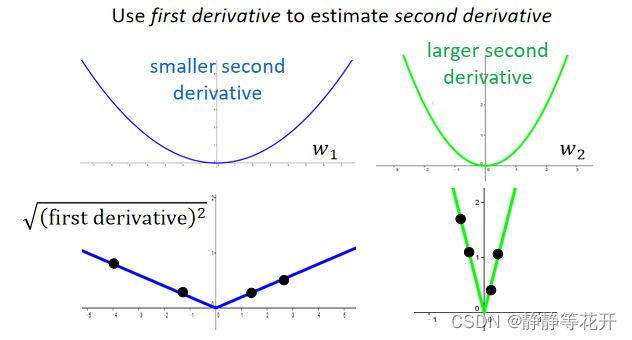
根据上图,当二阶导数比较小时,他的一阶导数通常也比较小;当二阶导数比较大时,他的一阶导数通常也比较大。所有可以通过采样一阶导数去估计二阶导数大小。
Stochastic Gradient Descent(随机梯度下降法)
(1)普通梯度下降的损失函数:
Loss Function对每个训练案例都要考虑。
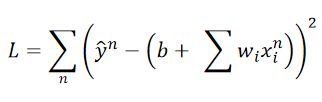
普通梯度下降的参数update:
update过程中每一个训练案例都会被考虑到
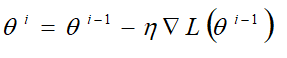
(2)Stochastic Gradient Descent
损失函数:
只考虑一个example/输出案例。与普通梯度下降Loss function的区别是,去掉了最外层的求和,因为只有一个example。
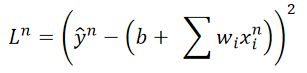
随机梯度下降的参数update:
update过程中只考虑一个example,每输入一个example更新一次
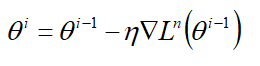
下降过程对比:
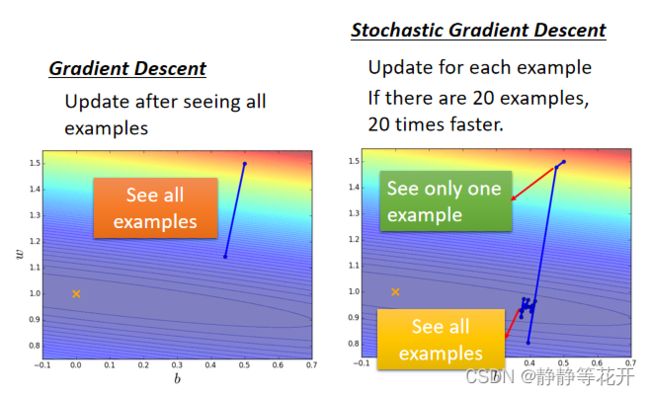
因为随机梯度下降在遇到每一个example都会update一次,所以下降的会相对比较快。
Feature Scaling(特征缩放)
当两个输入的feature分布的范围相差比较大时,可以进行特征缩放,让两个输入feature分布范围范围相差不大。

为什么呢?
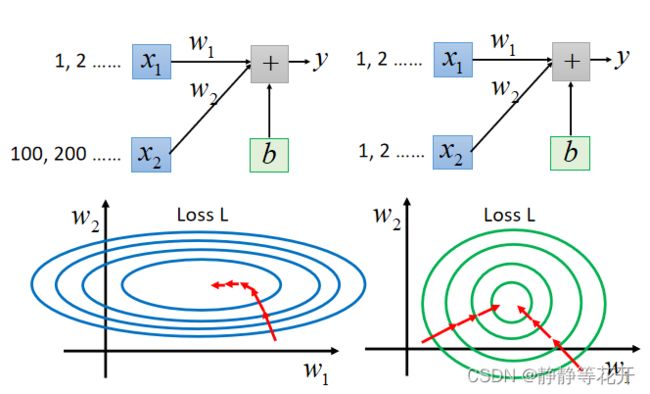
上图左边是未特征缩放前,输出的结果y会很大程度依赖于x2,Loss 在梯度下降时不会向中心下降,因为w2和w1对于Loss的贡献不同,所以w1和w2下降过程中会走些弯路。
右边是特征值缩放后,在下降过程中w1和w2对于Loss贡献差不多,所以在下降过程中大致朝着中心下降,少走些弯路。
数学角度看梯度下降
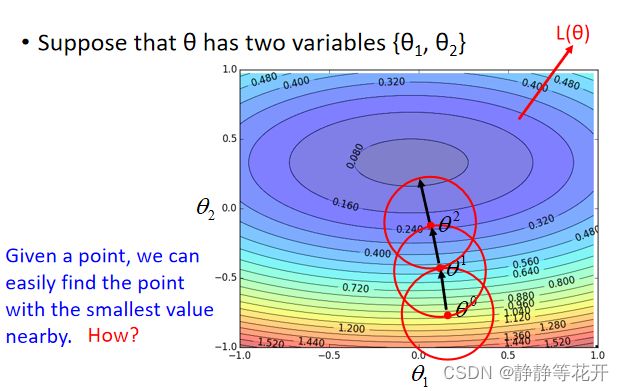
从图上看,其实就只在θ的附近进行探索Loss最低点,一步一步挪向最低点。
由泰勒级数,可以将函数写成:

当x无限接近x0,可以把函数缩写为:
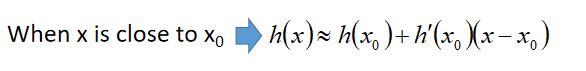
若有两个参数呢?如下图

在回到开始的那张图,当红圈足够小,就可以使用泰勒级数来替换Loss Function。

当(θ1,θ2)无限接近(a,b),将Loss function写成:
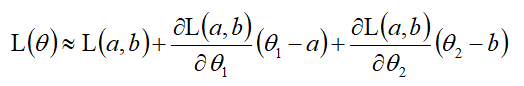
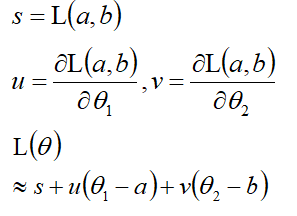
我们要做的是在红圈里面找最低点,所以 (θ1-a)2+(θ2-b)2≤d2
对于L(θ),u,v,s是常数,所以找最小值只看θ1和θ2。
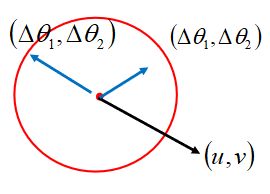
(θ1,θ2)什么情况下会使Loss最小呢?
 显然,(△θ1,△θ2)与(u,v)反向时,Loss最小。
显然,(△θ1,△θ2)与(u,v)反向时,Loss最小。
最后提出一个问题:每一次更新参数,获得的参数都会使 L(θ)更小吗?
不会,因为有时候你步子迈大了,方向使朝着最低点去,但是未必能上到最低点,也有迈过“山谷”可能往“山峰”上走了。