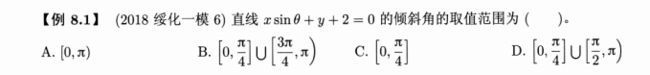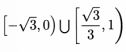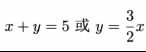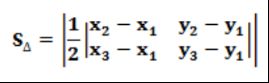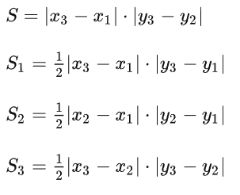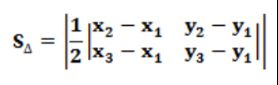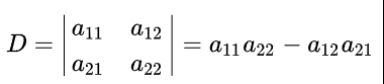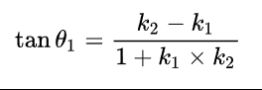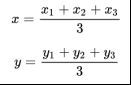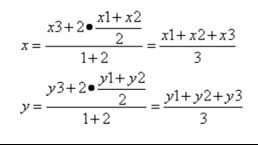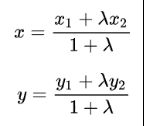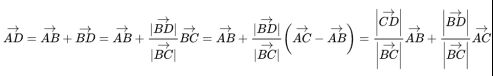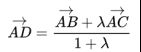【新高掌读书笔记】平面几何与三角函数 8.1 直线的有关概念与性质
目录
8.1 直线的有关概念与性质
8.1.1直线的方程
8.1.2两直线的位置关系
两直线平行与垂直
直线的交点坐标与距离公式
对称性问题
曲线关于点对称、关于直线对称
- 三角形三点面积公式
- 到角公式
- 定比分点坐标公式
- 定比分点向量形式
- 中点坐标公式(定比分点坐标公式的特殊情形)
- 三角形重心坐标公式(定比分点坐标公式的特殊情形)
-
8.1 直线的有关概念与性质
![]()
利用三角函数的有界性
先利用tan的无定义点分割角度范围的区间
再利用tan函数在周期内的单调性
![]()
利用a²的有界性
![]()
一定要画图,在平面直角坐标系中标记出各个点,画得尽量精确一些。
此外一定要考虑斜率不存在的情况
-
8.1.1直线的方程
![]()
已知直线上一点坐标,只要再求出斜率,就可以得到直线的点斜式方程
注意最后答题时,要化成一般式方程再作答
![]()
注意在设直线方程的时候,一定要考虑某种形式的方程不能表示的情况。如,截距式方程,不能表示过原点或垂直于坐标轴的直线。如果此题不考虑特殊情况,直接用截距式方程解题,就会出现漏解
因此,要养成习惯,在设直线方程时,要先考虑特殊情况是否符合题意。
另外需要注意截距的概念。截距并不是距离,我们把直线与坐标轴交点的横坐标(纵坐标)叫做直线在坐标轴上的截距.。截距可以为正数也可以为负数,还可以为零。再次强调,截距是横/纵坐标,而不是距离
本题需要使用两次中点坐标公式,求出两个中点的坐标
得到两点坐标后,可使用两点式得到直线方程。
事实上,截距式方程由于本身就是倒数和为定值的形式,因此常与基本不等式结合。解题方法一般就是乘一法。
-
8.1.2两直线的位置关系
两直线平行与垂直
![]()
做这类问题前,要先判断两直线斜率不存在的情况
由于这两条直线平行,如果斜率不存在情况成立,就意味着两直线斜率都不存在,即两条直线y前面的系数都为0
但是直线L1的y前面的系数不为零,显然斜率存在,此情况排除
在排除了斜率不存在的特殊情况后,我们再通过两条直线斜率相等解出a的值
做这类问题前,要先判断两直线斜率不存在的情况
由于直线L1方程y前面的系数不为零,斜率一定存在。所以只有可能是L2的斜率不存在。但是L2斜率不存在时,L1并不平行于x轴,因此两直线并不平行。该情况排除。
在排除了斜率不存在的特殊情况后,我们再通过两条直线斜率之积为-1解出a的值
![]()
做这类问题前,要先判断两直线斜率不存在的情况
设P(0,y),如果MP或NP斜率不存在,就意味着P与M或者N的横坐标相同。这显然不成立
在排除了斜率不存在的特殊情况后,我们再通过两条直线斜率之积为-1解出P的坐标
对于集合M,它表示方程为y=3x-3且不经过点(2,3)的直线。因此要满足N和M的交集为空集,即直线ax+2y+a=0与直线y=3x-3平行;或直线ax+2y+a=0与直线y=3x-3不平行,但直线ax+2y+a=0经过点(2,3)
直线的交点坐标与距离公式
解法一:解出两直线交点坐标得到直线L上一点坐标,在根据斜率之积为-1解出直线L的斜率k,最后用点斜式表示直线
解法二:使用直线系方程
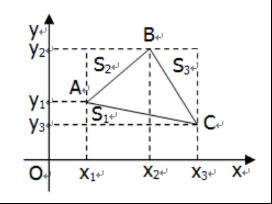
解法一:三角形三个定点中有两个定点一个动点。将两定点所在的边确定为底,用两点间距离公式算出底的长度;设出动点坐标,带入点到直线距离公式,计算出动点到已知底边的距离H,即为高。将求出的底边长度和对应高的表达式带入三角形面积公式,已知面积为10,可解出动点坐标
解法二:三角形三点面积公式,即向量外积坐标公式
下面推导此公式
设三角形三点坐标![]()
显然![]()
化简得到![]()
为了方便记忆,表示为行列式形式。二阶行列式的计算方法为对角线法则
其中行列式的第一行可以看作是向量AB的坐标,第二行可以看作向量AC的坐标
如此记忆十分方便
实际上是求一对平行直线的对称轴的问题
其对称轴是与这对平行直线平行且到这对平行直线距离相等的直线
解法一:设对称轴直线方程为x+y+m=0,再带入两平行线距离公式求解
解法二:事实上,这一共三条直线方程的x、y前系数一致时,常数项C成等差数列
![]()
注意数形结合
解法一:
- 根据两腰直线方程解出顶点A坐标
- 设出底边所在直线L(斜率为k1),即一条过原点的直线
- L分别与两条腰所在直线联立,解出另外两个三角形顶点B、C坐标
- 根据中点坐标公式,解出两个顶点B、C的中点D坐标
- 求出D点和顶点A所在直线的斜率k2
- 根据等腰三角形底边三线合一,k1*k2=-1
- 解出两个值,但以上仅仅表示底边所在直线经过原点,并不意味着底边所在线段经过原点
- 根据底边线段是否经过原点排除掉一个解,最终只有一解符合题意
解法二:到角公式
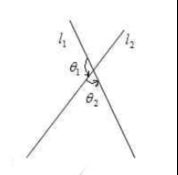
需要注意的是,到角与夹角不相同。“到角”是带有方向的角,故叫有向角。而夹角只有大小,没有方向。
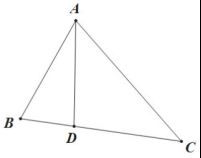
如图,直线L1和直线L2相交于一点,把L1绕该点按逆时针旋转θ1角,此时两直线重合,θ1角就叫做从L1到L2的角,同理,θ2就叫做从L2到L1的角
注意分子:终边斜率-始边斜率
利用到角公式求对称直线:
对称性问题
两点关于直线对称:
- 两点连线中点在对称轴上
- 两点所在直线与对称轴垂直
这里涉及到三角形的重心坐标公式
下面证明一下:
设三角形三个顶点A,B,C坐标依次为(x1,y1),(x2,y2),(x3,y3)
三角形ABC重心G坐标为(x,y)
则重心G在以AB为底的中线CM上
根据中点坐标公式,M的坐标为
![]()
由重心性质:重心到顶点的距离与重心到对边中点的距离之比为2:1
根据定比分点坐标公式,得到
定积分点坐标公式
在两点连线上有一点P,设它的坐标为(x,y),且![]()
我们称P为定比分点,且
下面证明定比分点坐标公式
以上就是向量三点共线定理的证明过程
由此,我们得到了定比分点公式的向量形式
我们在平面直角坐标系中,对![]()
运用定比分点公式的向量形式,即可得到定比分点坐标公式
定比分点坐标公式的形式与向量形式的很相近
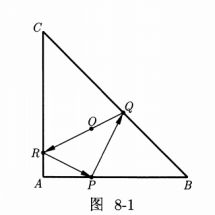
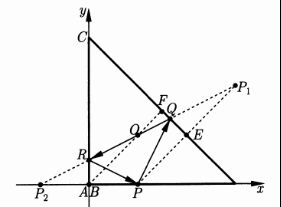
回到本题,建立平面直角坐标系
根据三角形三个顶点的坐标,不难求出其重心的坐标
设P点坐标为(m,0)
通过利用对称找出P关于斜边的对称点P1和关于y轴的对称点P2
此时点Q、R所在直线相当于是直线P1P2
根据两点式表示出直线方程
再将重心坐标带入
最后解出参数m即可
曲线关于点对称、关于直线对称
基本思路:先用未知曲线方程上的点作为参数,利用对称,表示出已知曲线上的点,再代入已知曲线方程并化简,即可得到未知曲线的方程
![]()
![]()
一般来说,有几个动点就用几次对称
找出对称点之后再用两点间距离公式