机器学习|K邻近回归模型预测实战|python应用

K邻近回归模型python应用

感谢各位小伙伴看到这里，或许看见代码各位脑袋都大了，啊哈哈
这篇文章很简短，大多数是代码，没有对原理或者代码进行解读，仅仅给小伙伴提供一种思路和方法，希望小伙伴们有所得！
如果对K邻近原理或者代码有更多的兴趣，请大家点赞或者收藏，题主会对大家的呼声进行回应哦！

如果小伙伴引用我的代码，请附上来源，谢谢！
转载请附上来源，谢谢！

1.加载csv数据

def load_orindata():
# load dataset
    dataset = read_csv('paperuse.csv',sep=',')
    return dataset

2.孤立森林检测异常值

def Cheak_VF(data):
    clf=IsolationForest()
    pres=clf.fit_predict(trans_data)
    return pres

3.检查离散值状态

def obser_nominal_vars(nominal_vars,testdata):
    nominal_vars=nominal_vars
    testdata=testdata
    for each in nominal_vars:
        print(each, ':')
        print(testdata[each].agg([‘value_counts’]).T)
        print('='*35)

4.分类标签编码

处理离散值的一般性方法

def lable_trans(testdata,lable_nominal_vars):
    testdata = testdata
    object_cols_lable=lable_nominal_vars
    label_encoder = LabelEncoder()
    for col in object_cols_lable:
        testdata[col]= label_encoder.fit_transform(testdata[col])
    return testdata

5.热独码编码

热独码对于离散值有比较优秀的表现，但题主建议小类别不超过10

def one_hot_trans(object_cols_onehot,testdata):
    object_cols_onehot = object_cols_onehot
    testdata = testdata
    OH_encoder = OneHotEncoder(handle_unknown='ignore', sparse=False)
    OH_cols_train = pd.DataFrame(OH_encoder.fit_transform(testdata[object_cols_onehot]))
    OH_cols_train.columns = OH_encoder.get_feature_names_out(input_features=object_cols_onehot)
    num_X_train = testdata.drop(object_cols_onehot, axis=1)
    OH_X_train = pd.concat([num_X_train, OH_cols_train], axis=1)
    #     x=testdata.iloc[:, 0:10].values
    #     y=testdata.iloc[:,10:11].values
    return OH_X_train

6.分割数据集

def split_test_train(data,train_size):
    data=data
    train_size=train_size
    features = data.drop('OR', axis=1)
    training_features, testing_features, training_target, testing_target =                               train_test_split(features.values, data['OR'].values, random_state=42,train_size=train_size)
    return training_features, testing_features, training_target, testing_target,features

7.构建K邻近回归模型

name='kneighbormodel'
kneighbormodel=KNeighborsRegressor()
print('开始训练模型：'+ name)
kneighbormodel.fit(training_features,training_target)
train_prey_KNeighborsRegressor=kneighbormodel.predict(training_features)
y_pred_KNeighborsRegressor=kneighbormodel.predict(testing_features)  
TestRecomValues(testing_target,y_pred_KNeighborsRegressor,name)
TrainRecomValues(training_target,train_prey_KNeighborsRegressor,name)
all_y,all_prey_KNeighborsRegressor = collection_data(training_target,testing_target,train_prey_KNeighborsRegressor,y_pred_KNeighborsRegressor)

8.模型评价函数

值得注意的是，分类和回归问题采用不同的评价方法，一定不能混用！此处题主进行的是回归模型预测！！常用的5个回归模型评价指标。

def TestRecomValues(testing_target,results,model_name):
  model_name=model_name
  r2_test = r2_score(testing_target,results)
  MAE_test = mean_absolute_error(testing_target,results)
  MSE_test = mean_squared_error(testing_target,results) 
  MAPE_test = mean_absolute_percentage_error(testing_target,results)
  RMSE_test = np.sqrt(mean_squared_error(testing_target,results))
  print(f'model_name : {model_name}\nr2_test = {r2_test}\nMAE_test = {MAE_test}\nMSE_test = {MSE_test}\nMAPE_test = {MAPE_test}\nRMSE_test = {RMSE_test}\n')

终端输出，如果需要美观的表格，可输出到文档或者开发HTML获取数据

开始训练模型：kneighbormodel
model_name : kneighbormodel
r2_test = 0.9222065243506832
MAE_test = 1.3888414911329112
MSE_test = 6.040082026483679
MAPE_test = 0.10867874402440293
RMSE_test = 2.4576578334836765

9.训练集和测试集合并函数

此处合并并非必要，而是为了下文整体数据集绘图做准备。

def collection_data(training_target,testing_target,train_prey,y_pred):
    training_target=pd.DataFrame(training_target)
    testing_target=pd.DataFrame(testing_target)
    train_prey=pd.DataFrame(train_prey)
    y_pred=pd.DataFrame(y_pred)
    all_y= np.vstack([training_target, testing_target])
    all_prey= np.vstack([train_prey, y_pred])
    return all_y,all_prey

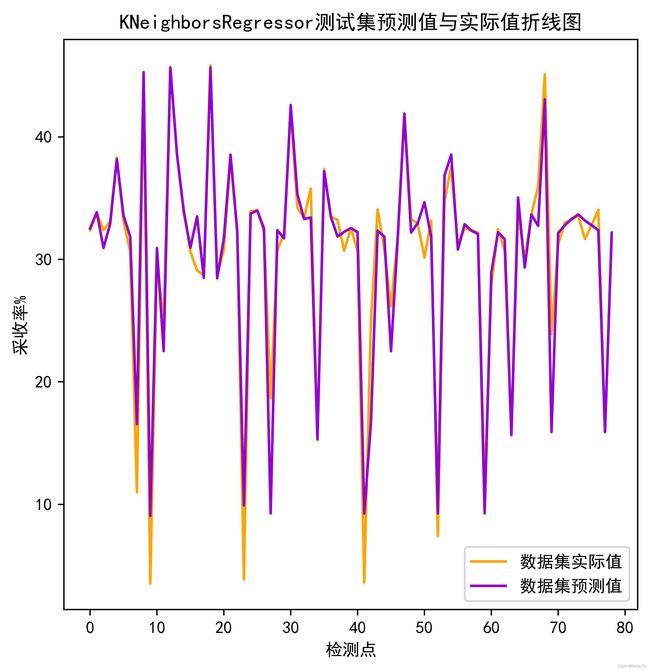
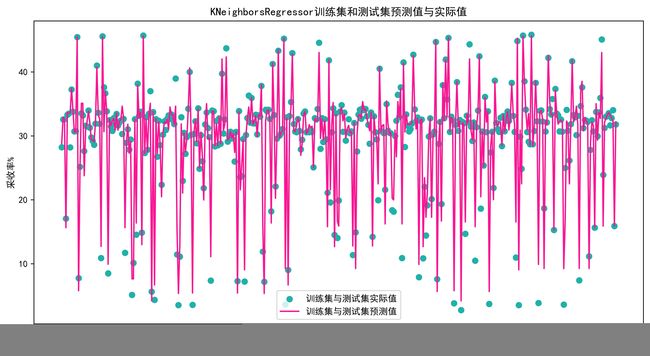
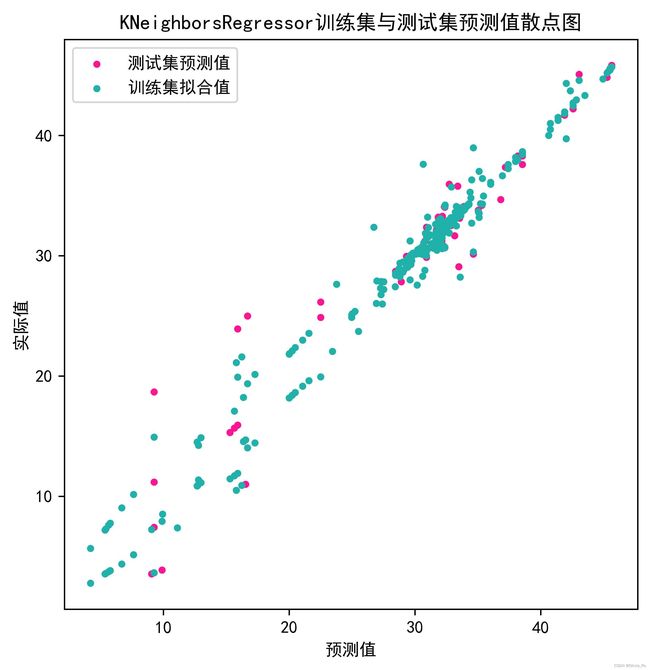
10.绘制图像

DrawPredRealValueLineChart(testing_target,y_pred,(6,6),'KNeighborsRegressor')
Scatter_Line(all_y,all_prey,(12,6),'KNeighborsRegressor')
ScatterPreReal(y_pred,testing_target,train_prey,training_target,(6,6),'KNeighborsRegressor')

def DrawPredRealValueLineChart(all_y,all_prey,figsize,modelname):
    plt.figure(figsize=figsize)
    q=range(0,len(all_y))
    plt.plot(q, all_y, color='orange', label='数据集实际值')
    plt.plot(q, all_prey, color='darkviolet', label='数据集预测值')
    plt.xlabel("检测点") #x轴命名表⽰
    plt.ylabel("采收率%") #y轴命名表⽰
    plt.title("{}测试集预测值与实际值折线图".format(modelname)) 
    plt.legend()
    plt.savefig(r'C:\pu\fig\{}DrawPredRealValueLineChart.jpg'.format(modelname), bbox_inches='tight', dpi=800)
    plt.show()

def Scatter_Line(all_y,all_prey,figsize,modelname):
    plt.figure(figsize=figsize)
    q=range(0,len(all_y))
    plt.scatter(q,all_y,color='lightseagreen', label='训练集与测试集实际值')
    plt.plot(q, all_prey,color='deeppink', label='训练集与测试集预测值')
    plt.xlabel("检测点") #x轴命名表⽰
    plt.ylabel("采收率%") #y轴命名表⽰
    plt.title("{}训练集和测试集预测值与实际值".format(modelname)) 
    plt.legend()
    plt.savefig(r‘C:\pu\fig\{}Scatter_Line.jpg'.format(modelname), bbox_inches='tight', dpi=800)
    plt.show()

def ScatterPreReal(results,testing_target,training_pre,training_target,figsize,modelname):
    #结果对比    
    plt.figure(figsize=figsize)
    plt.scatter(results,testing_target,marker='o',s=10,c='deeppink',label='测试集预测值')
    plt.scatter(training_pre,training_target,marker='o',s=10,c='lightseagreen',label='训练集拟合值')
    plt.title('{}训练集与测试集预测值散点图'.format(modelname))
    plt.xlabel('预测值')
    plt.ylabel('实际值')
    plt.legend()
    plt.savefig(r'C:\pu\fig\{}ScatterPreReal.jpg'.format(modelname), bbox_inches='tight', dpi=800)
    plt.show()

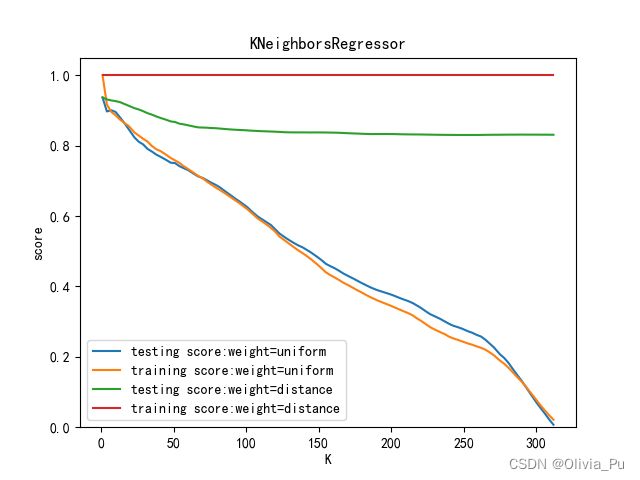
12.先验值优化参数

def test_KNeighborsRegressor_k_w(*data):
    '''
    测试 KNeighborsRegressor 中 n_neighbors 和 weights 参数的影响
    '''
    X_train,X_test,y_train,y_test=data
    Ks=np.linspace(1,y_train.size,num=100,endpoint=False,dtype='int')
    weights=['uniform','distance']
    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    ### 绘制不同 weights 下， 预测得分随 n_neighbors 的曲线
    for weight in weights:
        training_scores=[]
        testing_scores=[]
        for K in Ks:
            regr=KNeighborsRegressor(weights=weight,n_neighbors=K)
            regr.fit(X_train,y_train)
            testing_scores.append(regr.score(X_test,y_test))
            training_scores.append(regr.score(X_train,y_train))
        ax.plot(Ks,testing_scores,label="testing score:weight=%s"%weight)
        ax.plot(Ks,training_scores,label="training score:weight=%s"%weight)
    ax.legend(loc='best')
    ax.set_xlabel("K")
    ax.set_ylabel("score")
    ax.set_ylim(0,1.05)
    ax.set_title("KNeighborsRegressor")
    plt.show()

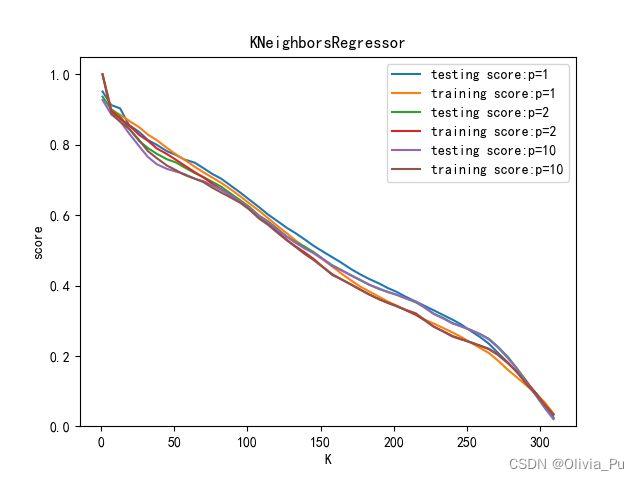
12.先验值优化参数2

def test_KNeighborsRegressor_k_p(*data):
    '''
    测试 KNeighborsRegressor 中 n_neighbors 和 p 参数的影响
    '''
    X_train,X_test,y_train,y_test=data
    Ks=np.linspace(1,y_train.size,endpoint=False,dtype='int')
    Ps=[1,2,10]
    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    ### 绘制不同 p 下， 预测得分随 n_neighbors 的曲线
    for P in Ps:
        training_scores=[]
        testing_scores=[]
        for K in Ks:
            regr=KNeighborsRegressor(p=P,n_neighbors=K)
            regr.fit(X_train,y_train)
            testing_scores.append(regr.score(X_test,y_test))
            training_scores.append(regr.score(X_train,y_train))
        ax.plot(Ks,testing_scores,label="testing score:p=%d"%P)
        ax.plot(Ks,training_scores,label="training score:p=%d"%P)
    ax.legend(loc='best')
    ax.set_xlabel("K")
    ax.set_ylabel("score")
    ax.set_ylim(0,1.05)
    ax.set_title("KNeighborsRegressor")
    plt.show()

12.先验值优化参数3

def best_n_neighbor(*data):
    X_train,X_test,y_train,y_test=data
    result={}
    for i in range(100):#一般n_neighbors的选取低于样本总数的平方根
        knn=KNeighborsRegressor(n_neighbors=(i+1))
        knn.fit(X_train,y_train)
        prediction=knn.predict(X_test)
        score=r2_score(y_test,prediction)
        result[i+1]=score*100
    for i in result.keys():
        if result[i]==max(result.values()):
            print("最佳邻近数："+str(i))
    print("模型评分："+str(max(result.values())))

12.优化参数4

机器学习库自带的优化函数，如果大家感兴趣可以留言，我将更新。值得注意的是当数据庞大时，网格搜索需要更好的计算机性能，比如GPU的支持。对于中型及以上规模的数据或者一般性能的计算机，题主不建议进行网格搜索，因为机器训练时间将会非常非常非常长。超参数的选择带来的性能提升是比较小的。

1. 网格搜索GridSearchCV
2. 随机搜索RandomizedSearchCV
3. hyperopt

13.优化参数重新建模

与上文相似，只需要将优化的参数代入模型即可。

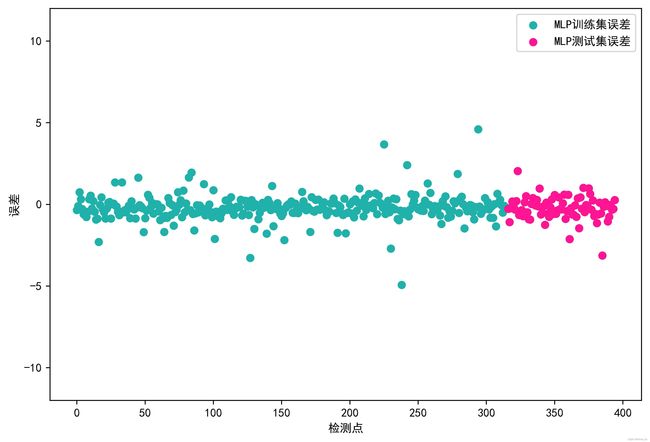
14.检验误差及分布

如果大家感兴趣可以留言，我将会更新代码。举个栗子，下面的图片所表达的是MLP模型，即多重感知机的误差，而非K邻近回归模型。
海绿色点表示训练集误差，深粉色表示测试集误差。
黑线表示正态分布，柱体表示误差，红色虚线表示核密度曲线。

题主个人介绍

小可爱一只，本科软件工程，研究生xxxx，双非。
希望小伙伴们在学习路上有所得，永远年轻，永远热泪盈眶！