论文笔记（一）《Intriguing properties of neural networks》

对抗样本（一）《Intriguing properties of neural networks》

神经网络的有趣特性
两点：
性质1：单个的深层神经元与随机线性组合的多个深层神经元并没有什么差别——这意味着深层神经网络的语义信息（某一种特征）并非单独存在于某一个神经元中，而是分布于整个空间（多个神经元共同存在某种特征信息）。
性质2：深层神经网络的输入输出映射（input-output mappings）具有显著的不连续性。我们可以通过应用某种难以察觉的扰动，使网络对图像进行错误分类。

对抗性样本
1.来源：是通过优化输入以使预测误差最大化来发现的
2.特点：相对健壮，并且作用于具有不同层数、激活或训练在训练数据的不同子集上的神经网络。
3.通过反向传播学习的深度神经网络具有非直观的特征和固有的盲点，其结构与数据分布的关系不明显

Units of: φ(x)（证明性质1）
先前技术：
检查特征空间的各个坐标，并将它们与输入域中的有意义的变化联系起来（就是说我们可以将提取的特征与输入图像联系起来，知道特征的改变对应着输入图像的何种变化），类似的推理（输入与特征联系）在之前的工作中被用于分析处理计算机视觉的神经网络，他们认为网络的一个激活值就代表一个有意义的特征。他们寻找输入图像，以最大化这个激活值。这类工作可以被称为t图像x ′ 的视觉检测，其中x ′ 要满足(或接近可达到的最大值)：

其中I是留出未作为模型训练的一组图像数据，ϕ(x)代表网络某一层的激活值， e i代表该第i 个值为1其余值为0的自然基向量;<.>代表内积。这个式子代表我们在 I 中找到使得ϕ(x)所在层第i 个神经元激活值达到最大的图片。

本实验技术：
对于任何一个随机方向v ∈ R n都会产生相似的可解释的语义属性。也就是说，我们发现了图像x ′在语义上彼此是相关的，则有：

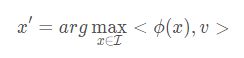
这就表明对于检测ϕ(x)的属性自然基并不比随机的向量基要好。这让神经网络在不同坐标间解开变异因素的想法受到了质疑（基于v 找到的图片x ′ 之间的相似性与基于e i 找到的x ′ 之间的相似性相差不多。这表明基于一个神经元e i 的语义解释性与基于一组神经元线性组合v的语义解释性相差不多)。
使用在MNIST上训练的卷积神经网络来评估上述声明。我们对I使用MNIST测试集。图1显示了在自然基础上最大化激活的图像，图2显示了在随机方向上最大化激活的图像。在这两种情况下，得到的图像有许多高层次的相似之处。
我们在AlexNet上重复了我们的实验，其中我们使用了验证集I。图3和图4比较了训练后的网络上的自然基和随机基。这些行似乎对单个单元和单元组合都具有语义意义。
尽管这样的分析可以洞察φ在特定情况下产生不变性的能力,作为输入分布的子集，它不能解释其域的其他部分的行为。

Blind Spots in Neural Networks神经网络的盲点
对于一个足够小的半径 ε > 0 在一个给定的训练输入x附近，一个满足 ||r|| < ε 的x + r将被分配一个高概率的正确类的模型。这种平滑先验（平滑先验理解见文末参考网址）对计算机视觉问题是有效的。一般来说，给定图像的微小扰动通常不会改变底层类。

公式

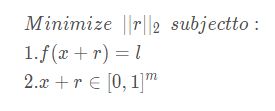
最小值（微小扰动）r 可能不是唯一的，但是对于任意选择的最小值r 用D(x,l)表示这样的x + r 。也就是说，*x+r是与f 分类为l 的x 最接近的图像。*显然，D(x,f(x))=f(x),所以，只有当f ( x ) ≠ l 时次任务才是有意义的。一般来说，准确的计算D(x,l)是比较困难的问题，所以用约束L-BFGS方法近似的计算。具体来说，通过进行线搜索（line-search）找到使得极小值r 满足f ( x + r ) = l 的最小值c > 0 从而得到D ( x , l ) 的近似值。

原文链接：https://blog.csdn.net/xiaokan_001/article/details/113831438

实验结果

上面每副图片的左侧是真实的图片，中间是加的噪音（就是优化问题中的r），右边是生成的对抗样本图片。很好笑的是，6张对抗样本全部被错分类为了鸵鸟！！
所以，这里已经解决了怎么找对抗样本的问题，但是没有深入到问题的本质，为什么能够找到？能找到我们不意外，因为我们总可以在原来的图片上“动手术”，让他改成我们要的样子，但是Szegedy的实验很出人意料，因为结果显示其实只需要很微小的扰动就能随意改变分类的标签，这又是为什么？
下面我们再继续讨论，首先先看goodfellow是怎么总结现有结论的：

• 使用Box-constrained L-BFGS能够找到对抗样本
• 在ImageNet这样的数据集里，对抗样本和原始样本的差别非常小，人眼不可分别
• 同样的对抗样本，会同时被不同的分类器错误分类，哪怕他们使用了不同的训练集 浅层的softmax回归模型对对抗样本也很脆弱
• 在对抗样本上训练能够正则化模型，但是代价高昂，因为训练集不容易获得。

注意最后一条，大家可能在想，我们手动生成对抗样本喂给分类器学习不就完了吗，但是效果并不好，因为对抗样本的生成比较expensive。如果我们能知道对抗样本产生的原因，也许能更轻松的制造对抗样本，从而训练。

“最小近似”函数D DD具有以下有趣的属性，在本节中通过非正式证据和定量实验来支持这些属性：
1.对于研究的所有网络（MNIST，QuocNet [10]，AlexNet [9]），对于每个样本，设法生成非常接近且在视觉上难以区分的对抗样本，这些样本会被原始网络错误分类（参见图 5，并以http://goo.gl/huaGPb为例）即，任意样本总可以找到对抗样本。
2.交叉模型泛化：相对较大一部分对抗样本将被具有不同超参数(层数、正则化或初始权重)的网络误分类。（这些对抗样本对很大一部分神经网络所有普适性，会导致网络出错）
3.交叉训练集泛化：同一网络在不同的训练集（不相交）训练（不是叠加训练，是重新训练参数）后，对抗样本同样也有效，即出现误分类。
说明对抗样本是具有“universal”的特性，而不是仅仅针对特殊的模型或对某一训练集的选择。也说明反过来用对抗样本加入训练集再训练会提高模型的泛化能力。

出于空间考虑，只给出了我们所进行的MNIST实验的一个代表子集（见表1）的结果。这里给出的结果与各种非卷积模型的结果是一致的。对于MNIST，还没有关于卷积模型的结果，但是通过对AlexNet的第一次定性实验让我们有理由相信卷积网络也可能表现出类似的行为。我们的每一个模型都用L-BFGS训练直到收敛。前三种模型是线性分类器，它们在像素级上进行，具有不同的权重衰减参数λ。我们的所有样本都对连接权重使用二次权重衰减：
再加上总损失，其中k 是层中的神经元数。三个模型是没有隐层（FC10（λ ）的简单线性（softmax）分类器。其中，FC10（1）被训练成极高的λ = 1，以测试在这种极端环境下是否仍有可能产生对抗样本。第二个模型是简单的具有两个隐层和一个分类器的sigmoidal神经网络。第三个模型AE400-10由一个具有sigmoid激活的单层稀疏自动编码器和一个带有Softmax分类器的400个节点组成。这个网络一直在训练，直到它得到非常高质量的第一层过滤器，而这一层并没有被微调。最后一列测量训练集中达到0%精度所需的最小平均像素失真。失真由原始图像x 和变形的x ′ 图像之间的
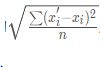度量，其中n = 784是图像的像素数。也就是像素强度缩放到[0，1]之间。

译文参考：
https://blog.csdn.net/qq_35024702/article/details/105687109?spm=1001.2101.3001.6650.8&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7ERate-8.pc_relevant_paycolumn_v3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7ERate-8.pc_relevant_paycolumn_v3&utm_relevant_index=10