LeetCode 2038. 如果相邻两个颜色均相同则删除当前颜色 / 440. 字典序的第K小数字（类字典树思路） / 661. 图片平滑器

2038. 如果相邻两个颜色均相同则删除当前颜色

2022.3.22 每日一题

题目描述

总共有 n 个颜色片段排成一列，每个颜色片段要么是 ‘A’ 要么是 ‘B’ 。给你一个长度为 n 的字符串 colors ，其中 colors[i] 表示第 i 个颜色片段的颜色。

Alice 和 Bob 在玩一个游戏，他们 轮流 从这个字符串中删除颜色。Alice 先手 。

• 如果一个颜色片段为 ‘A’ 且 相邻两个颜色 都是颜色 ‘A’ ，那么 Alice 可以删除该颜色片段。Alice 不可以 删除任何颜色 ‘B’ 片段。
• 如果一个颜色片段为 ‘B’ 且 相邻两个颜色 都是颜色 ‘B’ ，那么 Bob 可以删除该颜色片段。Bob 不可以 删除任何颜色 ‘A’ 片段。
• Alice 和 Bob 不能 从字符串两端删除颜色片段。
• 如果其中一人无法继续操作，则该玩家 输 掉游戏且另一玩家 获胜 。

假设 Alice 和 Bob 都采用最优策略，如果 Alice 获胜，请返回 true，否则 Bob 获胜，返回 false。

示例 1：

输入：colors = “AAABABB”
输出：true
解释：
AAABABB -> AABABB
Alice 先操作。
她删除从左数第二个 ‘A’ ，这也是唯一一个相邻颜色片段都是 ‘A’ 的 ‘A’ 。

现在轮到 Bob 操作。
Bob 无法执行任何操作，因为没有相邻位置都是 ‘B’ 的颜色片段 ‘B’ 。
因此，Alice 获胜，返回 true 。

示例 2：

输入：colors = “AA”
输出：false
解释：
Alice 先操作。
只有 2 个 ‘A’ 且它们都在字符串的两端，所以她无法执行任何操作。
因此，Bob 获胜，返回 false 。

示例 3：

输入：colors = “ABBBBBBBAAA”
输出：false
解释：
ABBBBBBBAAA -> ABBBBBBBAA
Alice 先操作。
她唯一的选择是删除从右数起第二个 ‘A’ 。

ABBBBBBBAA -> ABBBBBBAA
接下来轮到 Bob 操作。
他有许多选择，他可以选择任何一个 ‘B’ 删除。

然后轮到 Alice 操作，她无法删除任何片段。
所以 Bob 获胜，返回 false 。

提示：

1 <= colors.length <= 10^5
colors 只包含字母 ‘A’ 和 ‘B’

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/remove-colored-pieces-if-both-neighbors-are-the-same-color
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

相通就好了，很简单

class Solution {
    public boolean winnerOfGame(String colors) {
        //因为只能连续的删除，所以问题的关键就是有多少个连续的A或者B
        
        int l = colors.length();

        int a = 0;
        int b = 0;
        int x = 0;
        int y = 0;
        for(int i = 0; i < l; i++){
            char c = colors.charAt(i);
            if(c == 'A'){
                a++;
                b = 0;
                if(a >= 3){
                    x++;
                }
            }else{
                b++;
                a = 0;
                if(b >= 3){
                    y++;
                }
            }
        }
        return x > y;
    }
}

440. 字典序的第K小数字

2022.3.23 每日一题

题目描述

给定整数 n 和 k，返回 [1, n] 中字典序第 k 小的数字。

示例 1:

输入: n = 13, k = 2
输出: 10
解释: 字典序的排列是 [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9]，所以第二小的数字是 10。

示例 2:

输入: n = 1, k = 1
输出: 1

提示:

1 <= k <= n <= 10^9

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/k-th-smallest-in-lexicographical-order
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

就是个字典树的思路，不过不太好写
简而言之就是说，例如先统计 数字1 下面在n范围内的子树，总共有多少个节点，例如有count个
然后将count和k相比较，如果count大于等于k，说明要找的第k个节点在这个子树下面，那么就沿着这颗子树往下找，需要的操作呢，就是将当前数乘以10，就到了这颗子树的下一层

如果count小于k，那么说明当前子树包含的节点都在第k个节点之前，所以直接遍历下一颗子树

这里为了能够直接输出idx，在开头将k先减去1

class Solution {
    public int findKthNumber(int n, int k) {
        //首先要找到第k个数的前缀，然后再在这个前缀里找到第k个数
        //那么如何找到，例如前缀为1的数有多少个呢
        //例如给n为132，找第52个数
        //那么1开头的，1,10,11,12,13,14..，两位数是没问题的，
        //当3位数的时候，如果n大于199，那么也可以直接跳过，统计100个
        //但是如果n小于等于199，那么就需要考虑了
        //所以可以得到每个前缀的数的范围，然后统计

        //表示几开头
        int idx = 1;
        k--;
        while(k != 0){
            int num = idx;
            int step = 0;
            long left = num;
            long right = num; 
            //如果左边小于n，那么说明可以向下延伸该树，例如1 10-19 100-199
            while(left <= n){
                step += Math.min(right, n) - left + 1;
                left *= 10;
                right = right * 10 + 9;
            }
            //如果当前范围内数小于k个，说明第k个数在新子树下面，跳过当前子树的step个节点
            //否则遍历当前子树
            if(step <= k){
                idx++;
                k -= step;
            }else{
                //乘以10到达当前子节点
                idx *= 10;
                k--;        //只减去当前节点的数
            }
        }
        return idx;
    }
}

这个是没有开始k–的

class Solution {
    public int findKthNumber(int n, int k) {
        //首先要找到第k个数的前缀，然后再在这个前缀里找到第k个数
        //那么如何找到，例如前缀为1的数有多少个呢
        //例如给n为132，找第52个数
        //那么1开头的，1,10,11,12,13,14..，两位数是没问题的，
        //当3位数的时候，如果n大于199，那么也可以直接跳过，统计100个
        //但是如果n小于等于199，那么就需要考虑了
        //所以可以得到每个前缀的数的范围，然后统计

        //表示几开头
        long idx = 1;
        while(k != 0){
            long num = idx;
            int step = 0;
            long left = num;
            long right = num; 
            //如果左边小于n，那么说明可以向下延伸该树，例如1 10-19 100-199
            while(left <= (long)n){
                step += Math.min(right, n) - left + 1;
                left *= 10;
                right = right * 10 + 9;
            }
            //如果当前范围内数小于k个，说明第k个数在新子树下面，跳过当前子树的step个节点
            //否则遍历当前子树
            if(step < k){
                idx++;
                k -= step;
            }else{
                //乘以10到达当前子节点
                idx *= 10;
                k--;        //只减去当前节点的数
            }
        }
        return (int)(idx / 10);
    }
}

661. 图片平滑器

2022.3.24 每日一题

题目描述

图像平滑器 是大小为 3 x 3 的过滤器，用于对图像的每个单元格平滑处理，平滑处理后单元格的值为该单元格的平均灰度。

每个单元格的 平均灰度 定义为：该单元格自身及其周围的 8 个单元格的平均值，结果需向下取整。（即，需要计算蓝色平滑器中 9 个单元格的平均值）。

如果一个单元格周围存在单元格缺失的情况，则计算平均灰度时不考虑缺失的单元格（即，需要计算红色平滑器中 4 个单元格的平均值）。

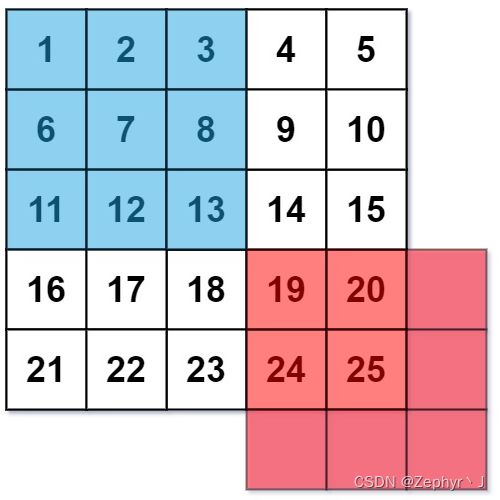
给你一个表示图像灰度的 m x n 整数矩阵 img ，返回对图像的每个单元格平滑处理后的图像 。

示例 1:

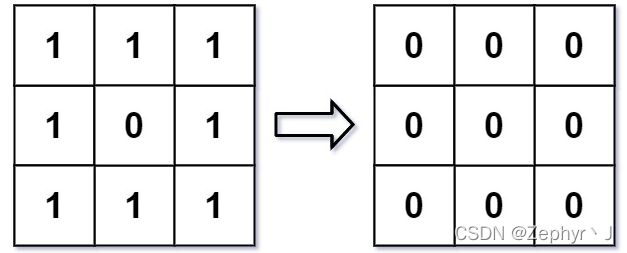
输入:img = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[0, 0, 0],[0, 0, 0], [0, 0, 0]]
解释:
对于点 (0,0), (0,2), (2,0), (2,2): 平均(3/4) = 平均(0.75) = 0
对于点 (0,1), (1,0), (1,2), (2,1): 平均(5/6) = 平均(0.83333333) = 0
对于点 (1,1): 平均(8/9) = 平均(0.88888889) = 0

示例 2:

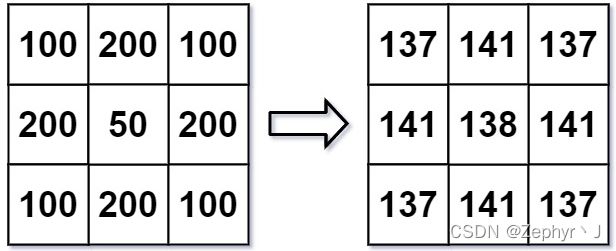
输入: img = [[100,200,100],[200,50,200],[100,200,100]]
输出: [[137,141,137],[141,138,141],[137,141,137]]
解释:
对于点 (0,0), (0,2), (2,0), (2,2): floor((100+200+200+50)/4) = floor(137.5) = 137
对于点 (0,1), (1,0), (1,2), (2,1): floor((200+200+50+200+100+100)/6) = floor(141.666667) = 141
对于点 (1,1): floor((50+200+200+200+200+100+100+100+100)/9) = floor(138.888889) = 138

提示:

m == img.length
n == img[i].length
1 <= m, n <= 200
0 <= img[i][j] <= 255

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/image-smoother
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

class Solution {
    int[][] dir = {{0,1}, {0,-1}, {1,0}, {-1,0}, {1,1}, {1, -1}, {-1, 1}, {-1, -1}, {0,0}};
    public int[][] imageSmoother(int[][] img) {
        //感觉是想方法不如直接算系列
        int m = img.length;
        int n = img[0].length;

        int[][] res = new int[m][n];
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                int count = 0;
                for(int[] d : dir){
                    int x = i + d[0];
                    int y = j + d[1];
                    if(x >= 0 && x < m && y >= 0 && y < n){
                        res[i][j] += img[x][y];
                        count++;
                    }
                }
                res[i][j] /= count;
            }
        }
        return res;
    }
}

看到一个有意思的题解，就是怎么用原地算法来求解
思路是这样的，因为题目给到的数目不大，9个数加起来再平均，也不会超过2的八次方
那么就可以把这个平均数，放到当前位置数的高八位，然后将矩阵处理完，再放到第八位
就没有使用额外空间完成了
这种方法有点巧妙，学习一下

class Solution {
    int[][] dirs = {{-1, -1}, {-1, 0}, {-1, 1}, {0, -1}, {0, 1}, {1, -1}, {1, 0}, {1, 1}};
    public int[][] imageSmoother(int[][] img) {
        int R = img.length, C = img[0].length;
        for (int r = 0; r < R; ++r)
            for (int c = 0; c < C; ++c) {
                int sum = img[r][c], cnt = 1;
                for (int k = 0; k < dirs.length; ++k) {
                    int nr = r + dirs[k][0], nc = c + dirs[k][1];
                    if (nr < 0 || nr > R - 1 || nc < 0 || nc > C - 1) continue;
                    sum += (img[nr][nc] & 0x00FF);
                    cnt++;
                }
                sum /= cnt;
                //System.out.println(sum);
                img[r][c] |= sum << 8;
            }

        for (int r = 0; r < R; ++r)
            for (int c = 0; c < C; ++c)
                img[r][c] >>= 8;
        return img;
    }
}

最好的方法还是前缀和了
矩阵的前缀和，用右下角的前缀和，减去右上角和左下角的前缀和，加上左上角的前缀和

class Solution {
    public int[][] imageSmoother(int[][] img) {
        int m = img.length, n = img[0].length;
        int[][] sum = new int[m + 10][n + 10];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + img[i - 1][j - 1];
            }
        }
        int[][] ans = new int[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                int a = Math.max(0, i - 1), b = Math.max(0, j - 1);
                int c = Math.min(m - 1, i + 1), d = Math.min(n - 1, j + 1);
                int cnt = (c - a + 1) * (d - b + 1);
                int tot = sum[c + 1][d + 1] - sum[a][d + 1] - sum[c + 1][b] + sum[a][b];
                ans[i][j] = tot / cnt;
            }
        }
        return ans;
    }
}