【深度学习进阶-自然语言处理】第一章:神经网络的复习
本章复习了神经网络的基础知识,“从零开始搭建”一个神经网络模型对一个简单数据集进行神经网络的学习。
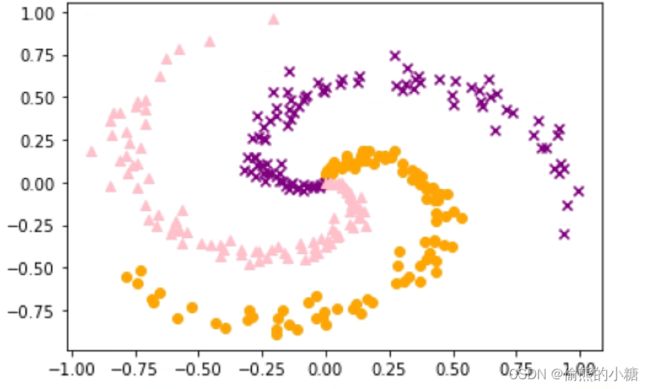
1.数据集
先看一下数据集:
该数据一共300行,x是输入数据,t是标签,是一个三维的one-hot向量。
#读入数据
import sys
sys.path.append("..")
from dataset import spiral
x,t = spiral.load_data()
print('x',x.shape) #x (300, 2)
print('t',t.shape) #t (300, 3)
2.神经网络的实现
下面实现一个具有一个隐藏层的神经网络。
class TwoLayerNet:
def __init__(self,input_size,hidden_size,output_size):
I,H,O = input_size,hidden_size,output_size
#初始化权重和偏置
W1 = 0.01 * np.random.randn(I,H) #形状:I*H
b1 = np.zeros(H)
W2 = 0.01 * np.random.randn(H,O)
b2 = np.zeros(O)
#生成层
self.layers = [
Affine(W1,b1),
Sigmoid(),
Affine(W2,b2)
]
#Softmax With Loss层和其他层的处理方式不同
#所以不将它放在layers列表中,而是单独存储在变量loss_layer中
self.loss_layer = SoftmaxWithLoss()
self.params,self.grads = [],[]
for layer in self.layers:
self.params += layer.params
self.grads += layer.grads
def predict(self,x):
for layer in self.layers:
x = layer.forward(x)
return x
def forward(self,x,t):
score = self.predict(x)
loss = self.loss_layer.forward(score,t)
return loss
def backward(self,dout = 1):
dout = self.loss_layer.backward(dout)
for layer in reversed(self.layers):
dout = layer.backward(dout)
return dout
3.学习过程+结果
#1.设定超参数
max_epoch = 300
batch_size = 30
hidden_size = 10
learning_rate = 1.0
#2.读入数据,生成模型和优化器
x,t = spiral.load_data()
model = TwoLayerNet(input_size=2,hidden_size=hidden_size,output_size=3)
optimizer = SGD(lr=learning_rate)
#学习用的变量
data_size = len(x)
max_iters = data_size // batch_size
total_loss = 0
loss_count = 0
loss_list = []
for epoch in range(max_epoch):
#3.打乱数据
idx = np.random.permutation(data_size)
x = x[idx]
t = t[idx]
for iters in range(max_iters):
batch_x = x[iters*batch_size:(iters+1)*batch_size]
batch_t = t[iters*batch_size:(iters+1)*batch_size]
#4.计算梯度,更新参数
loss = model.forward(batch_x,batch_t)
model.backward()
optimizer.update(model.params,model.grads)
total_loss += loss
loss_count += 1
#5.定期输出学习过程
if (iters+1)%10 == 0:
avg_loss = total_loss / loss_count
print('| epoch %d | iter %d / %d | loss %0.2f'% (epoch+1,iters + 1,max_iters,avg_loss))
loss_list.append(avg_loss)
total_loss,loss_count = 0,0
运行上面的代码,可以看出输出的损失值在训练过程中平稳下降,将结果画出来,如图所示:
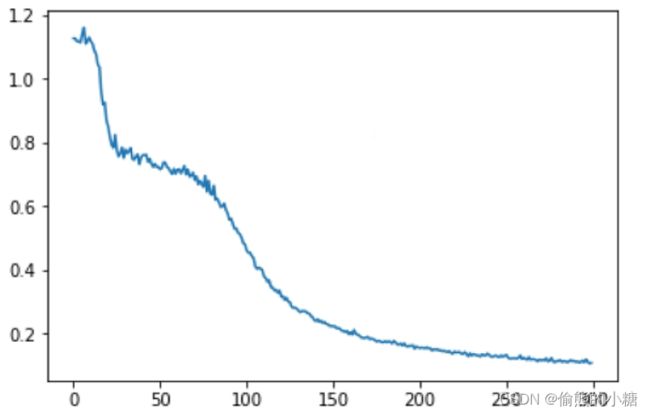 将学习后的决策边界画出,如图所示:
将学习后的决策边界画出,如图所示:

4.Affine层
计算图:
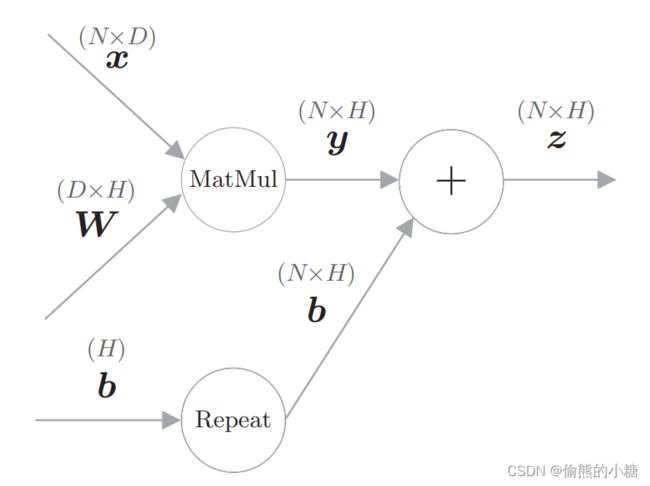 代码实现:
代码实现:
没有用matmul,用的np.dot(说是为了复习,行)
class Affine:
def __init__(self,W,b):
self.params = [W,b] #保存参数
self.grads = [np.zeros_like(W),np.zeros_like(b)] #保存梯度
self.x = None
def forward(self,x):
W,b = self.params
out = np.dot(x,W) + b
self.x = x
return out
def backward(self,dout):
W,b = self.params
dx = np.dot(dout,W.T)
dW = np.dot(self.x.T,dout)
db = np.sum(dout,axis=0)
self.grads[0][...] = dW #[...]对应的覆盖类似于深拷贝
self.grads[1][...] = db
return dx
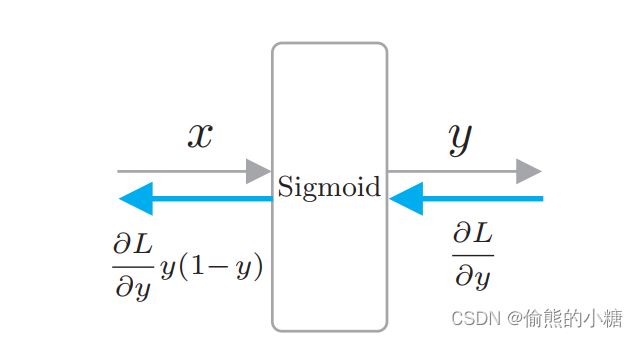
5.Sigmoid层
class Sigmoid:
def __init__(self):
self.params = []
self.grads = []
self.out = None
def forward(self,x):
out = 1 / (1 + np.exp(-x))
self.out = out
return out
def backward(self,dout):
dx = dout * (1.0 - self.out) * self.out
return dx
6.Softmax With Loss层
def softmax(x):
if x.ndim == 1:
x = x - np.max(x)
x = np.exp(x)/np.sum(np.exp(x))
elif x.ndim == 2:
x = x - x.max(axis = 1,keepdims = True)
x = np.exp(x)
x /= x.sum(axis=1, keepdims=True)
return x
def cross_entropy_error(y,t):
if y.ndim == 1:
t = t.reshape(1,t.size)
y = y.reshape(1,y.size)
#因为监督标签是one-hot-vector形式,所以这里要取下标
if t.size == y.size:
t = t.argmax(dim=1)
batch_size = y.shape[0]
#没看懂为啥
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
class SoftmaxWithLoss:
def __init__(self):
self.params = []
self.grads = []
self.y = None #softmx的输出
self.t = None #监督标签
def forward(self,x,t):
self.t = t
self.y = softmax(x)
if self.t.size == self.y.size:
self.t = self.t.argmax(axis=1)
loss = cross_entropy_error(self.y,self.t)
return loss
def backward(self,dout =1):
batch_size = self.t.shape[0]
dx = self.y.copy()
dx[np.arange(batch_size),self.t] -= 1
dx *= dout
dx = dx/batch_size
return dx
关于这里的交叉熵函数(cross_entropy_error),《深度学习入门》这本书中提到了两种实现的方式:
(1)监督数据为one-hot形式

(2)监督数据为标签形式(直接是“2”“3”这样的标签)
 所以这里是用了argmax提取到one-hot向量中的下标作为标签,然后使用第二种方式进行计算。(行)
所以这里是用了argmax提取到one-hot向量中的下标作为标签,然后使用第二种方式进行计算。(行)
7.SGD层
class SGD:
'''
随机梯度下降法(Stochastic Gradient Descent)
'''
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for i in range(len(params)):
params[i] -= self.lr * grads[i]