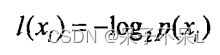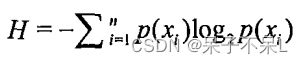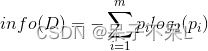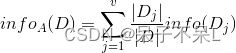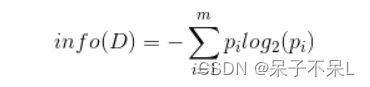机器学习 —— DecisionTree决策树

决策树的优缺点

优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据。既能用于分类，也能用于回归

缺点：可能会产生过度匹配问题 (过拟合)

一、决策树的原理

【二十个问题的游戏】

游戏的规则很简单：参与游戏的一方在脑海里想某个事物，其他参与者向他提问题，只允许提20个问题，问题的答案也只能用对或错回答。问问题的人通过推断分解，逐步缩小待猜测事物的范围。决策树的工作原理与20个问题类似，用户输人一系列数据 ，然后给出游戏的答案。

我们经常使用决策树处理分类问题。近来的调查表明决策树也是最经常使用的数据挖掘算法。它之所以如此流行，一个很重要的原因就是使用者基本上不用了解机器学习算法，也不用深究它是如何工作的。

如果以前没有接触过决策树，完全不用担心，它的概念非常简单。即使不知道它也可以通过简单的图形了解其工作原理。

决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友，于是有了下面的对话：

  女儿：多大年纪了？

  母亲：26。

  女儿：长的帅不帅？

  母亲：挺帅的。

  女儿：收入高不？

  母亲：不算很高，中等情况。

  女儿：是公务员不？

  母亲：是，在税务局上班呢。

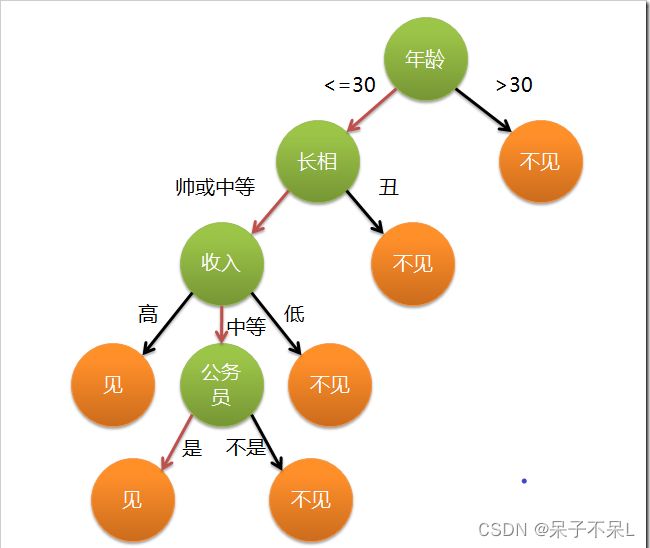
  女儿：那好，我去见见。

这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员将男人分为两个类别：见和不见。假设这个女孩对男人的要求是：30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员，那么这个可以用下图表示女孩的决策逻辑:

上图完整表达了这个女孩决定是否见一个约会对象的策略，其中绿色节点表示判断条件，橙色节点表示决策结果，箭头表示在一个判断条件在不同情况下的决策路径，图中红色箭头表示了上面例子中女孩的决策过程。

这幅图基本可以算是一颗决策树，说它“基本可以算”是因为图中的判定条件没有量化，如收入高中低等等，还不能算是严格意义上的决策树，如果将所有条件量化，则就变成真正的决策树了。

有了上面直观的认识，我们可以正式定义决策树了：

决策树（decision tree）是一个树结构（可以是二叉树或非二叉树）。其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。

可以看到，决策树的决策过程非常直观，容易被人理解。目前决策树已经成功运用于医学、制造产业、天文学、分支生物学以及商业等诸多领域。

之前介绍的K-近邻算法可以完成很多分类任务，但是它最大的缺点就是无法给出数据的内在含义，决策树的主要优势就在于数据形式非常容易理解。

决策树算法能够读取数据集合，构建类似于上面的决策树。决策树很多任务都是为了数据中所蕴含的知识信息，因此决策树可以使用不熟悉的数据集合，并从中提取出一系列规则，机器学习算法最终将使用这些机器从数据集中创造的规则。专家系统中经常使用决策树，而且决策树给出结果往往可以匹敌在当前领域具有几十年工作经验的人类专家。

知道了决策树的定义以及其应用方法，下面介绍决策树的构造算法。

二、决策树的构造

分类解决离散问题，回归解决连续问题

• 决策树：信息论
• 逻辑斯蒂回归、贝叶斯：概率论

不同于逻辑斯蒂回归和贝叶斯算法，决策树的构造过程不依赖领域知识，它使用属性选择度量来选择将元组最好地划分成不同的类的属性。所谓决策树的构造就是进行属性选择度量确定各个特征属性之间的拓扑结构。

构造决策树的关键步骤是分裂属性。所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支，其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。分裂属性分为三种不同的情况：

  1、属性是离散值且不要求生成二叉决策树。此时用属性的每一个划分作为一个分支。

  2、属性是离散值且要求生成二叉决策树。此时使用属性划分的一个子集进行测试，按照“属于此子集”和“不属于此子集”分成两个分支。

  3、属性是连续值。此时确定一个值作为分裂点split_point，按照>split_point和<=split_point生成两个分支。

构造决策树的关键性内容是进行属性选择度量，属性选择度量是一种选择分裂准则，它决定了拓扑结构及分裂点split_point的选择。

属性选择度量算法有很多，一般使用自顶向下递归分治法，并采用不回溯的贪心策略。这里介绍常用的ID3算法。

ID3算法

划分数据集的大原则是：将无序的数据变得更加有序。

尽快把不确定的数据变得确定

我们可以使用多种方法划分数据集，但是每种方法都有各自的优缺点。组织杂乱无章数据的一种方法就是使用信息论度量信息，信息论是量化处理信息的分支科学。我们可以在划分数据之前使用信息论量化度量信息的内容。

在划分数据集之前之后信息发生的变化称为信息增益，知道如何计算信息增益，我们就可以计算每个特征值划分数据集获得的信息增益，获得信息增益最高的特征就是最好的选择。

在可以评测哪种数据划分方式是最好的数据划分之前，我们必须学习如何计算信息增益。集合信息的度量方式称为香农熵或者简称为熵，这个名字来源于信息论之父克劳德•香农。

entropy熵

熵: 是>=0的值，越大表示不确定度越大， 越低表示不确定性越低（越确定）

熵定义为信息的期望值，在明晰这个概念之前，我们必须知道信息的定义。如果待分类的事务可能划分在多个分类之中，则符号x的信息定义为：

其中p(x)是选择该分类的概率

为了计算熵，我们需要计算所有类别所有可能值包含的信息期望值，通过下面的公式得到：

其中n是分类的数目。

在决策树当中，设D为用类别对训练元组进行的划分，则D的熵（entropy）表示为：

其中pi表示第i个类别在整个训练元组中出现的概率，可以用属于此类别元素的数量除以训练元组元素总数量作为估计。熵的实际意义表示是D中元组的类标号所需要的平均信息量。

现在我们假设将训练元组D按属性A进行划分，则A对D划分的期望信息为：

而信息增益即为两者的差值：

 

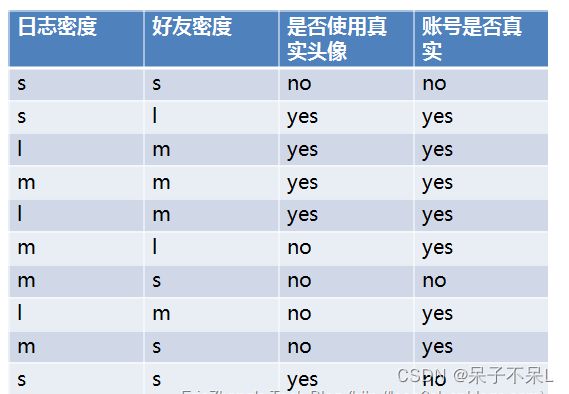
ID3算法就是在每次需要分裂时，计算每个属性的增益率，然后选择增益率最大的属性进行分裂。下面我们继续用SNS社区中不真实账号检测的例子说明如何使用ID3算法构造决策树。为了简单起见，我们假设训练集合包含10个元素：

 

其中s、m和l分别表示小、中和大。

设L、F和H表示日志密度、好友密度、是否使用真实头像，下面计算各属性的信息增益。

 

因此日志密度的信息增益是0.276。

用同样方法得到F和H的信息增益分别为0.553和0.033。

因为F具有最大的信息增益，所以第一次分裂选择F为分裂属性，分裂后的结果如下图表示：

 在上图的基础上，再递归使用这个方法计算子节点的分裂属性，最终就可以得到整个决策树。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

练习

计算上图的信息熵，确定下一个分类的特征

ID3算法

# D ：target 表示账号是否真实
# m ：结果类型数量
# 总共十条数据
# yes  7个   p = 7/10 = 0.7
# no 3个    p = 0.3

info_D = -(0.7 * np.log2(0.7) + 0.3 * np.log2(0.3))
info_D   # 0.8812908992306927

 每个特征的信息熵

日志密度L

# 日志密度有几个结果： 3个
# s ：3个  p=0.3  1个yes 2个no
# m ：4个  p=0.4  3个yes 1个no
# l ：3个  p=0.3  3个yes 0个no

infoL_D = 0.3 * (-( (1/3)*np.log2(1/3) + (2/3)*np.log2(2/3) ))\
        + 0.4 * (-( (3/4)*np.log2(3/4) + (1/4)*np.log2(1/4) ))
        # + 0.3 * (-( (3/3)*np.log2(3/3) + (0/3)*np.log2(0/3) ))
infoL_D   # 0.6

而信息增益即为两者的差值：

gain_L = info_D - infoL_D
gain_L

# 日志密度的信息增益：0.2812908992306927

 好友密度F

# 好友密度有几个结果： 3个
# s ：4个  p=0.4  1个yes 3个no
# m ：4个  p=0.4  4个yes 0个no
# l ：2个  p=0.2  2个yes 0个no

infoF_D = 0.4 * (-( (1/4)*np.log2(1/4) + (3/4)*np.log2(3/4) ))
        # + 0.4 * (-( (4/4)*np.log2(4/4) + (0/4)*np.log2(0/4) ))
        # + 0.2 * (-( (2/2)*np.log2(2/2) + (0/2)*np.log2(0/2) ))
infoF_D   # 0.32451124978365314


gain_F = info_D - infoF_D
gain_F

# 好友密度的信息增益：0.5567796494470396

是否使用真实头像H

# 是否使用真实头像有几个结果： 2个
# yes ：5个  p=0.5  4个yes 1个no
# no ：5个  p=0.5  3个yes 2个no

infoH_D = 0.5 * (-( (4/5)*np.log2(4/5) + (1/5)*np.log2(1/5) ))\
        + 0.5 * (-( (3/5)*np.log2(3/5) + (2/5)*np.log2(2/5) ))
infoH_D   # 0.8464393446710154


gain_H = info_D - infoH_D
gain_H

# 是否使用真实头像的信息增益：0.034851554559677256



# 信息增益：好友密度
#  会先将 好友密度 这个特征 作为优先分裂的特征



# ID3算法的缺点：
#  1. 如果有类似ID这种不存在重复值的特征列
#          1    1个    0.1    1yes 或 1no
#          2    1个    0.1    1yes 或 1no
#          ...
#          9    1个    0.1    1yes 或 1no
#          10    1个    0.1    1yes 或 1no
# infoID_D = 0.1 * ( - ( (1/1)*np.log2(1/1) + (0/1)*np.log2(0/1) ) )  * 10
# infoID_D  = 0

# ID信息增益：
# gainID = info_D - infoID_D
#            =  info_D  = 0.88

# 会优先按照ID来分裂： 但是像ID这种不重复的特征不应该作为优先分裂的特征

C4.5算法

• 解决的主要问题是： ID3算法中出现的ID属性的问题
• 单独计算每个特征的信息熵

日志密度L

# 日志密度单独的信息熵
# s p=0.3
# m p=0.4
# l p=0.3
info_L = -(0.3*np.log2(0.3) + 0.4*np.log2(0.4) + 0.3*np.log2(0.3))
info_L    # 1.5709505944546684



gain_L / info_L  #  0.17905776300262236

好友密度F

# 好友密度单独的信息熵
# s p=0.4
# m p=0.4
# l p=0.2
info_F = -(0.4*np.log2(0.4) + 0.4*np.log2(0.4) + 0.2*np.log2(0.2))
info_F   # 1.5219280948873621



gain_F / info_F   # 0.36583834106055246

是否使用真实头像H

# 是否使用真实头像单独的信息熵
# yes p=0.5
# no p=0.5
info_H = -(0.5*np.log2(0.5) + 0.5*np.log2(0.5))
info_H    # 1.0



gain_H / info_H    # 0.034851554559677256

ID

# ID 信息增益：
gain_ID = info_D
gain_ID   # 0.8812908992306927



# ID单独的信息熵
# 1 p=0.1
# 2 p=0.1
# ...
# 9 p=0.1
# 10 p=0.1
info_ID = -(0.1*np.log2(0.1) * 10)
info_ID    #  3.3219280948873626




gain_ID / info_ID   # 0.2652949955741215


# C4.5算法
#    好友密度 0.36 > ID 0.26 > 日志密度 0.17 > 是否使用真实头像0.03

# ID3算法
#    ID0.88 > 好友密度0.55 >日志密度 0.27 > 是否使用真实头像0.03

CART算法

• gini_D = 1 - sum( p(x)**2 )
• gini : 基尼， 基尼系数，作用类似信息熵

# 对比 对数 和 平方 时间差

%timeit np.log2(1000000)
# 966 ns ± 3.57 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)


%timeit 1000000**2
# 8.05 ns ± 0.0485 ns per loop (mean ± std. dev. of 7 runs, 100,000,000 loops each)


# D ：target 表示账号是否真实
# 总共十条数据
# yes  7个   p = 7/10 = 0.7
# no 3个    p = 0.3

gini_D = 1 - (0.7**2 + 0.3**2)
gini_D   # 0.42000000000000004

日志密度L

# 日志密度有几个结果： 3个
# s ：3个  p=0.3  1个yes 2个no
# m ：4个  p=0.4  3个yes 1个no
# l ：3个  p=0.3  3个yes 0个no

gini_L_D = 0.3 * (1 - ( (1/3)**2 + (2/3)**2))\
        + 0.4 * (1 - ( (3/4)**2 + (1/4)**2))\
        + 0.3 * (1 - ( (3/3)**2 + (0/3)**2))
gini_L_D   # 0.2833333333333333


# 信息增益
gini_D - gini_L_D   # 0.13666666666666671

好友密度F

# 好友密度有几个结果： 3个
# s ：4个  p=0.4  1个yes 3个no
# m ：4个  p=0.4  4个yes 0个no
# l ：2个  p=0.2  2个yes 0个no

gini_F_D = 0.4 * (1 - ( (1/4)**2 + (3/4)**2))\
        + 0.4 * (1 - ( (4/4)**2 + (0/4)**2))\
        + 0.2 * (1 - ( (2/2)**2 + (0/2)**2))
gini_F_D   # 0.15000000000000002



gini_D - gini_F_D   # 0.27

是否使用真实头像H

# 是否使用真实头像有几个结果： 2个
# yes ：5个  p=0.5  4个yes 1个no
# no ：5个  p=0.5  3个yes 2个no

gini_H_D = 0.5 * (1 - ( (4/5)**2 + (1/5)**2))\
        + 0.5 * (1 - ( (3/5)**2 + (2/5)**2))
gini_H_D   #  0.3999999999999999


gini_D - gini_H_D    # 0.02000000000000013




# 好友密度0.27 > 日志密度0.13 > 是否使用真实头像0.02

# 好友密度 优先分裂

三、实战

iris数据集

from sklearn.datasets import load_iris


data,target = load_iris(return_X_y=True)

data.shape   # (150, 4)

使用决策树算法

• from sklearn.tree import DecisionTreeClassifier

from sklearn.tree import DecisionTreeClassifier

• criterion='gini', gini系数， 默认使用CART算法，一般使用默认值

• splitter='best', 分割方式， 默认是best，最好的分割方式

• max_depth=None, 数的最大深度，数据量少的情况下不设置，默认没有限制深度，

  • 数据量大的情况下需要设置，防止过拟合

• min_samples_split=2, 最小分裂的样本数，数据量少的情况下不设置，默认是2

  • 数据量大的话，可以增加该值

• min_samples_leaf=1, 叶子节点所需要的最少样本数，

  • 如果叶子节点上的样本数小于该值，则会被剪枝(兄弟节点一般也会被剪枝)
  • 数据量不大的情况下，一般不设置，
  • 如果数据量比较大（上万）的时候考虑增加该值

# dt = DecisionTreeClassifier(max_depth=2)   # 防止过拟合将值调小
# dt = DecisionTreeClassifier(min_samples_split=4)   # 防止过拟合将值调大
# dt = DecisionTreeClassifier(min_samples_leaf=3)   # 防止过拟合将值调大
dt = DecisionTreeClassifier(min_samples_split=4,min_samples_leaf=3)

dt.fit(data,target).score(data,target)
# 0.98


# 特征重要性
dt.feature_importances_
# array([0.       , 0.       , 0.5736694, 0.4263306])

使用KNN算法

• from sklearn.neighbors import KNeighborsClassifier

from sklearn.neighbors import KNeighborsClassifier

knn = KNeighborsClassifier()
knn.fit(data,target).score(data,target)
# 0.9666666666666667

使用逻辑斯蒂回归算法

• from sklearn.linear_model import LogisticRegression

from sklearn.linear_model import LogisticRegression


lr = LogisticRegression(max_iter=1000)
lr.fit(data,target).score(data,target)
# 0.9733333333333334

使用决策树实现回归

• from sklearn.tree import DecisionTreeRegressor

from sklearn.tree import DecisionTreeRegressor

sin曲线

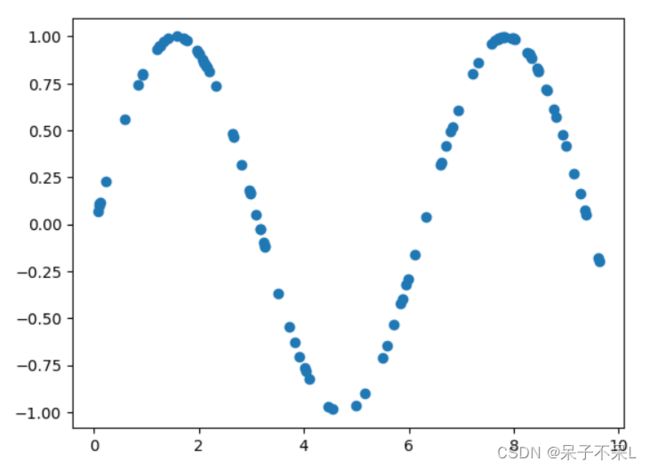
x_train = np.random.random(100)*10
y_train = np.sin(x_train)

plt.scatter(x_train,y_train)

 加噪声

y_train[::5] += np.random.random(20)*0.3
plt.scatter(x_train,y_train)

 

# 测试数据
x_test = np.linspace(0,10,100).reshape(-1,1)


# 决策树回归
tree = DecisionTreeRegressor()
tree.fit(x_train.reshape(-1,1),y_train)
y_tree = tree.predict(x_test)


# KNN 回归
from sklearn.neighbors import KNeighborsRegressor
knn = KNeighborsRegressor()
knn.fit(x_train.reshape(-1,1),y_train)
y_knn = knn.predict(x_test)


# 线性回归
from sklearn.linear_model import LinearRegression
linear = LinearRegression()
linear.fit(x_train.reshape(-1,1),y_train)
y_linear = linear.predict(x_test)


# 画图
plt.scatter(x_train,y_train)

plt.plot(x_test,y_tree,c='r',label='tree')
plt.plot(x_test,y_knn,c='g',label='KNN')
plt.plot(x_test,y_linear,c='y',label='Linear')

plt.legend()

随机森林

一个随机森林中包含多个决策树

分类问题: 对结果进行投票.

回归问题: 对结果进行平均

随机的含义:

1. 对样本进行随机, 样本的个数是一样的.

2. 对特征进行随机,特征数是一样的.

(1)数据的随机选取：

首先，从原始的数据集中采取有放回的抽样，构造子数据集，子数据集的数据是和原始数据集相同的。不同子数据集的元素可以重复，同一个子数据集中的元素也可以重复。第二，利用子数据集来构建子决策树，将这个数据放到每个子决策树中，每个子决策树输出一个结果。最后，如果有了新的数据需要通过随机森林得到分类结果，就可以通过对子决策树的判断结果的投票，得到随机森林的输出结果了。假设随机森林中有3棵子决策树，2棵子树的分类结果是A类，1棵子树的分类结果是B类，那么随机森林的分类结果就是A类。

(2)待选特征的随机选取

与数据集的随机选取类似，随机森林中的子树的每一个分裂过程并未用到所有的待选特征，而是从所有的待选特征中随机选取一定的特征，之后再在随机选取的特征中选取最优的特征。这样能够使得随机森林中的决策树都能够彼此不同，提升系统的多样性，从而提升分类性能。

随机森林算法

• from sklearn.ensemble import RandomForestClassifier

# ensemble：集成算法
from sklearn.ensemble import RandomForestClassifier


# n_estimators=100 : 决策树的数量，默认100个

# max_features='auto' ： 最大特征数
#  max_features : {"auto", "sqrt", "log2"}, int or float, default="auto"
#     The number of features to consider when looking for the best split:
#     - If int, then consider `max_features` features at each split.
#     - If float, then `max_features` is a fraction and
#       `round(max_features * n_features)` features are considered at each split.
#     - If "auto", then `max_features=sqrt(n_features)`.
#     - If "sqrt", then `max_features=sqrt(n_features)` (same as "auto").
#     - If "log2", then `max_features=log2(n_features)`.
#     - If None, then `max_features=n_features`.
#
# bootstrap = True :  有放回抽样
#
# max_samples : int or float, default=None  最大样本数
#     If bootstrap is True, the number of samples to draw from X
#     to train each base estimator.

#     - If None (default), then draw `X.shape[0]` samples.
#     - If int, then draw `max_samples` samples.
#     - If float, then draw `max_samples * X.shape[0]` samples. Thus,
#       `max_samples` should be in the interval `(0, 1)`.

rfc = RandomForestClassifier(n_estimators=100)
rfc.fit(data, target)

特征重要性

rfc.feature_importances_

# array([0.0938488 , 0.01775377, 0.44296768, 0.44542975])