图片相相似度计算(Hash、SSIM、compareHist)
哈希相似度算法(Hash algorithm)
用一个快速算法,就达到基本的效果。哈希算法(Hash algorithm),它的作用是对每张图片生成一个固定位数的Hash 值(指纹 fingerprint)字符串,然后比较不同图片的指纹,结果越接近,就说明图片越相似。一般有如下三种生成Hash 值方法:
差值DHash
- 缩小尺寸:将图片缩小到8x9的尺寸,总共72个像素。这一步的作用是去除图片的细节,只保留结构、明暗等基本信息,摒弃不同尺寸、比例带来的图片差异。
- 简化色彩:将缩小后的图片,转为64级灰度(或者256级也行)。
- 计算平均值:计算所有64个像素的灰度平均值。
- 比较:同行相邻间对比,像素值大于后一个像素值记作1,相反记作0。每行9个像素,8个差值,有8行共64位
- 计算哈希值:将上一步的比较结果,组合在一起,就构成了一个64位的整数,这就是这张图片的指纹。组合的次序并不重要,只要保证所有图片都采用同样次序就行了。
均值AHash
- 缩小尺寸:将图片缩小到8x8的尺寸,总共64个像素。这一步的作用是去除图片的细节,只保留结构、明暗等基本信息,摒弃不同尺寸、比例带来的图片差异。
- 简化色彩:将缩小后的图片,转为64级灰度。
- 计算平均值:计算所有64个像素的灰度平均值。
- 比较:像素值大于平均值记作1,相反记作0,总共64位。
- 计算哈希值:将上一步的比较结果,组合在一起,就构成了一个64位的整数,这就是这张图片的指纹。组合的次序并不重要,只要保证所有图片都采用同样次序就行了。
感知 PHash
感知哈希算法可以获得更精确的结果,它采用的是DCT(离散余弦变换)来降低频率。
- 缩小尺寸
为了简化了DCT的计算,pHash以小图片开始(建议图片大于8x8,32x32)。 - 简化色彩
与aHash相同,需要将图片转化成灰度图像,进一步简化计算量(具体算法见aHash算法步骤)。 - 计算DCT
DCT是把图片分解频率聚集和梯状形,将空域的信号转换到频域上,具有良好的去相关性的性能。变换后DCT系数能量主要集中在左上角,其余大部分系数接近于零,DCT具有适用于图像压缩的特性。 - 缩小DCT
DCT的结果为32x32大小的矩阵,但只需保留左上角的8x8的矩阵,这部分呈现了图片中的最低频率。 - 计算平均值
同均值哈希一样,计算8x8的DCT矩阵的均值 - 计算Phash值
根据8x8的DCT矩阵进行比较,大于等于DCT均值的设为”1”,小于DCT均值的设为“0”。组合成64个bit位生成hash值,顺序随意但前后保持一致性即可。
计算相似度(距离)
得到指纹以后,就可以对比不同的图片,看看64位中有多少位是不一样的。在理论上,这等同于计算汉明距离(Hamming distance)。如果不相同的数据位不超过5,就说明两张图片很相似;如果大于10,就说明这是两张不同的图片。
具体的代码实现python语言。
import cv2
import numpy as np
# 均值哈希算法
def aHash(img):
# 缩放为8*8
img = cv2.resize(img, (8, 8))
# 转换为灰度图
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# s为像素和初值为0,hash_str为hash值初值为''
s = 0
hash_str = ''
# 遍历累加求像素和
for i in range(8):
for j in range(8):
s = s + gray[i, j]
# 求平均灰度
avg = s / 64
# 灰度大于平均值为1相反为0生成图片的hash值
for i in range(8):
for j in range(8):
if gray[i, j] > avg:
hash_str = hash_str + '1'
else:
hash_str = hash_str + '0'
return hash_str
# 差值感知算法
def dHash(img):
img = cv2.resize(img, (9, 8))
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
hash_str = ''
# 每行前一个像素大于后一个像素为1,相反为0,生成哈希
for i in range(8):
for j in range(8):
if gray[i, j] > gray[i, j + 1]:
hash_str = hash_str + '1'
else:
hash_str = hash_str + '0'
return hash_str
# 感知哈希算法(pHash)
def pHash(img):
img = cv2.resize(img, (32, 32)) # , interpolation=cv2.INTER_CUBIC
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 将灰度图转为浮点型,再进行dct变换
dct = cv2.dct(np.float32(gray))
# opencv实现的掩码操作
dct_roi = dct[0:8, 0:8]
hash = []
avreage = np.mean(dct_roi)
for i in range(dct_roi.shape[0]):
for j in range(dct_roi.shape[1]):
if dct_roi[i, j] > avreage:
hash.append(1)
else:
hash.append(0)
return hash
# Hash值对比
def cmpHash(hash1, hash2):
n = 0
# hash长度不同则返回-1代表传参出错
if len(hash1)!=len(hash2):
return -1
# 遍历判断
for i in range(len(hash1)):
# 不相等则n计数+1,n最终为相似度
if hash1[i] != hash2[i]:
n = n + 1
return n
if __name__ == '__main__':
img1 = cv2.imread('./1.png')
img2 = cv2.imread('./2.png')
hash1 = aHash(img1)
hash2 = aHash(img2)
n = cmpHash(hash1, hash2)
print('均值哈希算法相似度:', n)
hash1 = dHash(img1)
hash2 = dHash(img2)
n = cmpHash(hash1, hash2)
print('差值哈希算法相似度:', n)
hash1 = pHash(img1)
hash2 = pHash(img2)
n = cmpHash(hash1, hash2)
print('感知哈希算法相似度:', n)
使用的时候,第一个参数是基准图片,第二个参数是用来比较的其他图片所在的目录,返回结果是两张图片之间不相同的数据位数量(汉明距离)。
这种算法的优点是简单快速,不受图片大小缩放的影响,缺点是图片的内容不能变更。如果在图片上加几个文字,它就认不出来了。
比较三种方法
- 均值Hash比感知显著地要快。如果你找一些明确的东西,均值Hash能算法快速地找到它,所以,它的最佳用途是根据缩略图,找出原图。
- 如果图片有些修改,如过都添加了一些内容或头部叠加在一起,均值Hash就无法处理,虽然感知Hash比较慢,但它能很好地容忍一些小的变型(变型度小于25%的图片)。
- 相比感知Hash,差值Hash的速度更快,
- 相比均值Hash,差值Hash在效率几乎相同的情况下的效果要更好
结构性相似度SSIM
在两幅图的距离时,更偏重于两图的结构相似性,而不是逐像素计算两图的差异。提出了基于 structural similarity 的度量,声称其比 MSE 更能反映人类视觉系统对两幅图相似性的判断。把两幅图 x, y 的相似性按三个维度进行比较:
亮度(对应均值)(luminance)l(x,y),
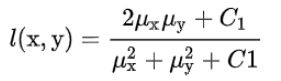
对比度(对应方差)(contrast)c(x,y),

结构(对应协方差)(structure)s(x,y),

令C3=C2/2,c(x,y)的分子和s(x,y)的分母可以约分,最终 x 和 y 的相似度为这三者的函数,默认每个项的重要性最后是相等的:
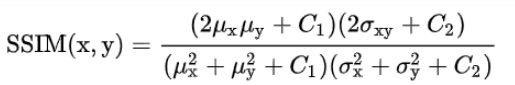
上述中 μ x , μ y , σ x , σ y , σ x y \mu{x},\mu{y},\sigma{x},\sigma{y},\sigma{xy} μx,μy,σx,σy,σxy分别为x图像均值,y图像均值,x图像方差,y图像方差,两图像协方差, C 1 , C 2 C1,C2 C1,C2为非零的小的常数避免分母为零。
通常, SSIM 不能用于一整幅图, 因为在整幅图的跨度上,均值和方差往往变化剧烈;同时,图像上不同区块的失真程度也有可能不同,不能一概而论;此外类比人眼睛每次只能聚焦于一处的特点。作者采用 sliding window 以步长为 1 计算两幅图各个对应 sliding window 下的 patch 的 SSIM,然后取平均值作为两幅图整体的 SSIM,称为 Mean SSIM。简写为 MSSIM(不同于multi-scale SSIM:MS-SSIM )。
如下为计算MSSIM的一种c++代码,使用了11*11的对称高斯加权函数作为加权窗口,标准差为1.5,C1 = 6.5025, C2 = 58.5225。
#include 直方图相似度函数compareHist
图像处理之相似图片识别函数compareHist包含了如下四种方法;
1;Correlation 相关性比较 [1,0] 越大越相似
2;Chi-Square 卡方比较 [0,+200] 越小越相似
3;Intersection 十字交叉性 [+50,0] 越大越相似
4;Bhattacharyya distance 巴氏距离 [0, 1] 越小越相似
算法概述:
首先对源图像与要筛选的图像进行直方图数据采集,对采集的各自图像直方图进行归一化;然后使用compareHist函数对直方图数据进行计算,最终得出图像相似度值。
第一步:直方图计算
直方图分为灰度直方图与RGB直方图,对于灰度图像直方图计算十分简单,只要初始化一
个大小为256的直方图数组H,然后根据像素值完成频率分布统计,假设像素值为124,则
H[124] += 1, 而对于彩色RGB像素来说直方图表达有两种方式,一种是单一直方图,另外一
种是三维直方图,三维直方图比较简单明了,分别对应RGB三种颜色,定义三个直方图HR,
HG, HB, 假设某一个像素点P的RGB值为(4, 231,129), 则对于的直方图计算为HR[4] += 1,
HG[231] += 1, HB[129] += 1, 如此对每个像素点完成统计以后,RGB彩色直方图数据就生成了。
而RGB像素的单一直方图SH表示稍微复杂点,每个颜色的值范围为0 ~ 255之间的,假设
可以分为一定范围等份,当8等份时,每个等份的值范围为32, 16等份时,每个等份值范
围为16,当4等份时候,每个等份值的范围为64,假设RGB值为(14, 68, 221), 16等份之
后,它对应直方图索引值(index)分别为: (0, 4, 13), 根据计算索引值公式:index = R + G16 + B16*16
对应的直方图index = 0 + 4*16 + 13 * 16 * 16, SH[3392] += 1
如此遍历所有RGB像素值,完成直方图数据计算。
第二步: 直接使用compareHist函数,选择合适参数计算即可
c++实现
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include python实现
from PIL import Image
def make_regalur_image(img, size = (256, 256)):
return img.resize(size).convert('RGB')
def hist_similar(lh, rh):
assert len(lh) == len(rh)
return sum(1 - (0 if l == r else float(abs(l - r))/max(l, r)) for l, r in zip(lh, rh))/len(lh)
def calc_similar(li, ri):
return hist_similar(li.histogram(), ri.histogram())
if __name__ == '__main__':
img1 = Image.open('./1.jpg')
img2 = Image.open('./2.jpg')
img1 = make_regalur_image(img1)
img2 = make_regalur_image(img2)
print(calc_similar(img1, img2))
总结
-
对比三种方法来说稳定性较好的是MSSIM方法,直方图过于简单,只能捕捉颜色信息的相似性,捕捉不到更多的信息。只要颜色分布相似,就会判定二者相似度较高,显然不合理。
-
基于互信息(Mutual Information)
如果两张图片尺寸相同,还是能在一定程度上表征两张图片的相似性的。但是,大部分情况下图片的尺寸不相同,如果把两张图片尺寸调成相同的话,又会让原来很多的信息丢失,应用中此种方法的确很难把握。 -
哈希算法
可以实现快速搜索简略图