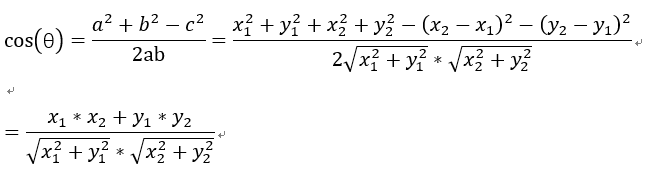相似度计算方法(三) 余弦相似度
一. 余弦相似度算法基本概念
余弦相似度算法:一个向量空间中两个向量夹角间的余弦值作为衡量两个个体之间差异的大小,余弦值接近1,夹角趋于0,表明两个向量越相似,余弦值接近于0,夹角趋于90度,表明两个向量越不相似。
二. 向量基本知识点
1 向量乘积公式
2 向量模计算公式
三. 余弦相似度计算数学原理
在工作中一直使用余弦相似度算法计算两段文本的相似度和两个用户的相似度。一直弄不明白多维的余弦相似度公式是怎么推导来的。今天终于花费时间把公式推导出来,其实很简单,都是高中学过的知识,只是很多年没用了,都还给老师了。本文还通过一个例子演示如果使用余弦相似度计算两段文本的相似度。
余弦函数在三角形中的计算公式为:
在直角坐标系中,向量表示的三角形的余弦函数是怎么样的呢?下图中向量a用坐标(x1,y1)表示,向量b用坐标(x2,y2)表示。
向量a和向量b在直角坐标中的长度为![]() 向量a和向量b之间的距离我们用向量c表示,就是上图中的黄色直线,那么向量c在直角坐标系中的长度为
向量a和向量b之间的距离我们用向量c表示,就是上图中的黄色直线,那么向量c在直角坐标系中的长度为![]() ,将a,b,c带入三角函数的公式中得到如下的公式:
,将a,b,c带入三角函数的公式中得到如下的公式:
这是2维空间中余弦函数的公式,那么多维空间余弦函数的公式就是:
余弦相似度
余弦相似度量:计算个体间的相似度。
相似度越小,距离越大。相似度越大,距离越小。
案例1、物品相似度计算
假设有3个物品,item1,item2和item3,用向量表示分别为:
item1[1,1,0,0,1],
item2[0,0,1,2,1],
item3[0,0,1,2,0],
即五维空间中的3个点。用欧式距离公式计算item1、itme2之间的距离,以及item2和item3之间的距离,分别是:
用余弦函数计算item1和item2夹角间的余弦值为:
用余弦函数计算item2和item3夹角间的余弦值为:
由此可得出item1和item2相似度小,两个之间的距离大(距离为7),item2和itme3相似度大,两者之间的距离小(距离为1)。
余弦相似度算法:一个向量空间中两个向量夹角间的余弦值作为衡量两个个体之间差异的大小,余弦值接近1,夹角趋于0,表明两个向量越相似,余弦值接近于0,夹角趋于90度,表明两个向量越不相似。
案例2、文本的相似度计算
思路:1、分词;2、列出所有词(可以处理停用词);3、分词编码;4、词频向量化;5、套用余弦函数计量两个句子的相似度。
第一步,分词。
句子A:这只/皮靴/号码/大了。那只/号码/合适。
句子B:这只/皮靴/号码/不/小,那只/更/合适。
第二步,列出所有的词。
这只,皮靴,号码,大了。那只,合适,不,小,很
第三步,计算词频。
句子A:这只1,皮靴1,号码2,大了1。那只1,合适1,不0,小0,更0
句子B:这只1,皮靴1,号码1,大了0。那只1,合适1,不1,小1,更1
第四步,写出词频向量。
句子A:(1,1,2,1,1,1,0,0,0)
句子B:(1,1,1,0,1,1,1,1,1)
到这里,问题就变成了如何计算这两个向量的相似程度。我们可以把它们想象成空间中的两条线段,都是从原点([0, 0, ...])出发,指向不同的方向。两条线段之间形成一个夹角,如果夹角为0度,意味着方向相同、线段重合,这是表示两个向量代表的文本完全相等;如果夹角为90度,意味着形成直角,方向完全不相似;如果夹角为180度,意味着方向正好相反。因此,我们可以通过夹角的大小,来判断向量的相似程度。夹角越小,就代表越相似。
使用上面的公式(4)
![]()
计算两个句子向量
句子A:(1,1,2,1,1,1,0,0,0)
和句子B:(1,1,1,0,1,1,1,1,1)的向量余弦值来确定两个句子的相似度。
计算过程如下:
![]()
计算结果中夹角的余弦值为0.81非常接近于1,所以,上面的句子A和句子B是基本相似的。
由此,我们就得到了文本相似度计算的处理流程是:
(1)找出两篇文章的关键词;
(2)每篇文章各取出若干个关键词,合并成一个集合,计算每篇文章对于这个集合中的词的词频
(3)生成两篇文章各自的词频向量;
(4)计算两个向量的余弦相似度,值越大就表示越相似。
案例3、购物网站文本的相似度计算
某购物网站有如下数据:小明购买了T恤a、T恤b、T恤e,小红购买了T恤b、T恤c、小强购买了T恤a、T恤e。
把以上信息转为向量图,代入上述的公式来计算得出相似度,过程如下:
由上述的结果便可得到如下结论:小明和小红这两个用户有一定的相似度,但是不大,因为他们只有一个共同商品;小明和小强这两个用户相似度最大,因为他们有两个共同商品;而小红和小强的相似度为0,因为小红买的T恤小强都没有买。