神经网络激活函数与求导
文章目录
-
-
- 神经网络激活函数求导
-
- 1、Sigmoid 激活函数
- 2、Tanh 激活函数
- 3、Softmax 激活函数
-
神经网络激活函数求导
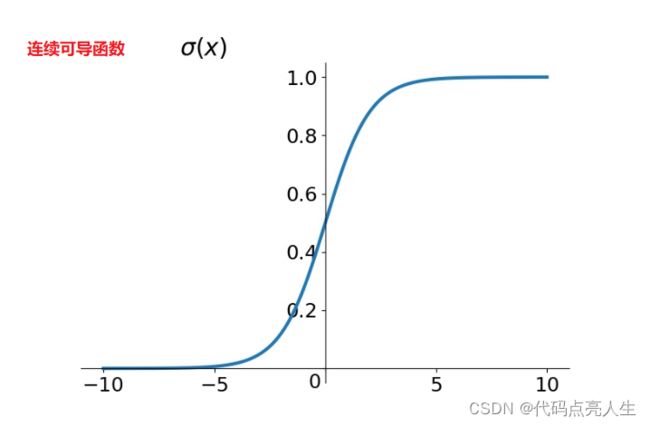
1、Sigmoid 激活函数
σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1
其导函数为:
σ ′ ( x ) = ∂ ∂ x 1 1 + e − x = e − x ( 1 + e − x ) 2 = 1 ( 1 + e − x ) 2 ⋅ e − x = 1 1 + e − x ⋅ ( 1 − 1 1 + e − x ) = σ ( x ) ⋅ ( 1 − σ ( x ) ) \begin{aligned} \sigma'(x) &= \frac{\partial}{\partial x}\frac{1}{1 + e^{-x}} \\\\&= \frac{e^{-x}}{(1 + e^{-x})^2}\\\\& = \frac{1}{(1 + e^{-x})^2}\cdot e^{-x}\\\\&=\frac{1}{1 + e^{-x}} \cdot (1 - \frac{1}{1 + e^{-x}})\\\\&=\sigma(x)\cdot (1 - \sigma(x))\end{aligned} σ′(x)=∂x∂1+e−x1=(1+e−x)2e−x=(1+e−x)21⋅e−x=1+e−x1⋅(1−1+e−x1)=σ(x)⋅(1−σ(x))
2、Tanh 激活函数
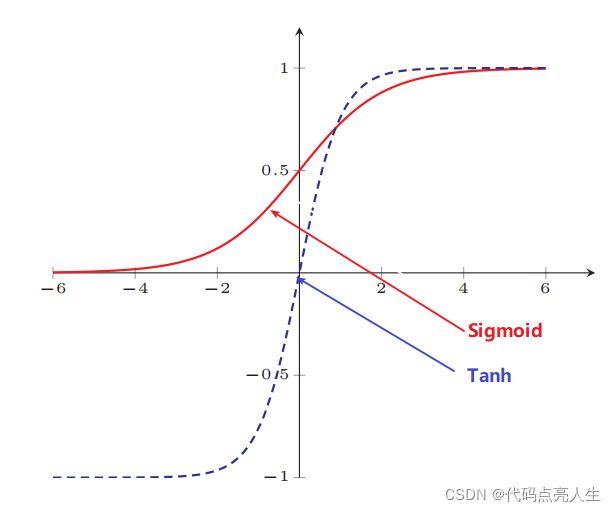
Tanh 函数可以看作是放大并平移的 Sigmoid 函数,但因为是零中心化的 (zero-centered) ,通常收敛速度快于 Sigmoid 函数,下图是二者的对比:
其函数形式为:
t a n h ( x ) = e x − e − x e x + e − x = 1 − e − 2 x 1 + e − 2 x = 2 − ( 1 + e − 2 x ) 1 + e − 2 x = 2 1 + e − 2 x − 1 = 2 σ ( 2 x ) − 1 \begin{aligned}tanh(x) &= \frac{e^x - e^{-x}}{e^x + e^{-x}} \\\\&= \frac{1 - e^{-2x}}{1 + e^{-2x}} \\\\&= \frac{2 - (1 + e^{-2x})}{1 + e^{-2x}} \\\\&= \frac{2}{1 + e^{-2x}} -1 \\\\&= 2\sigma(2x) - 1\end{aligned} tanh(x)=ex+e−xex−e−x=1+e−2x1−e−2x=1+e−2x2−(1+e−2x)=1+e−2x2−1=2σ(2x)−1
其导函数为:
t a n h ′ ( x ) = ( e x + e − x ) 2 − ( e x − e − x ) 2 ( e x + e − x ) 2 = 1 − t a n h 2 ( x ) \begin{aligned}tanh'(x) &= \frac{(e^x + e^{-x})^2 -(e^x - e^{-x})^2}{(e^x + e^{-x})^2} \\\\&= 1-tanh^2(x)\end{aligned} tanh′(x)=(ex+e−x)2(ex+e−x)2−(ex−e−x)2=1−tanh2(x)
3、Softmax 激活函数
Softmax 函数将多个标量映射为一个概率分布,其形式为:
y i = s o f t m a x ( z i ) = e z i ∑ j = 1 C e z j y_i = softmax(z_i) = \frac{e^{z_i}}{\sum\limits_{j=1}^{C}e^{z_j}} yi=softmax(zi)=j=1∑Cezjezi
y i y_i yi 表示第 i i i 个输出值,即属于类别 i i i 的概率, ∑ i = 1 C y i = 1 \sum\limits_{i = 1}^Cy_i = 1 i=1∑Cyi=1
z = W T x z = W^Tx z=WTx ,表示线性方程,Softmax 函数用于多分类,会对应多个方程。
首先求标量形式的导数,即第 i i i 个输出对于第 j j j 个输入的偏导数:
∂ y i ∂ z j = ∂ e z i ∑ j = 1 C e z j ∂ z j \frac{\partial y_i}{\partial z_j} = \frac{\partial \frac{e^{z_i}}{\sum\limits_{j=1}^{C}e^{z_j}}}{\partial z_j} ∂zj∂yi=∂zj∂j=1∑Cezjezi
其中 e z i e^{z_i} ezi 对 z j z_j zj 求导要分情况讨论:
∂ e z i ∂ z j = { e z i , i f i = j 0 , i f i ≠ j \frac{\partial e^{z_i}}{\partial z_j} = \left \{\begin{aligned} & e^{z_i}\ \ , \ \ & if \ \ i = j \\ &0\ \ ,\ \ &if \ \ i \not= j \end{aligned}\right. ∂zj∂ezi={ezi , 0 , if i=jif i=j
那么当 i = j i = j i=j 时:
∂ y i ∂ z j = e z i ∑ j = 1 C e z j − e z i e z j ( ∑ j = 1 C e z j ) 2 = e z i ∑ j = 1 C e z j − e z i ∑ j = 1 C e z j e z j ∑ j = 1 C e z j = y i − y i y j \begin{aligned}\frac{\partial y_i}{\partial z_j} &= \frac{e^{z_i}\sum\limits_{j=1}^Ce^{z_j} - e^{z_i}e^{z_j}}{(\sum\limits_{j=1}^Ce^{z_j})^2} \\\\&= \frac{e^{z_i}}{\sum\limits_{j=1}^Ce^{z_j}} - \frac{e^{z_i}}{\sum\limits_{j=1}^Ce^{z_j}}\frac{e^{z_j}}{\sum\limits_{j=1}^Ce^{z_j}} \\\\&= y_i - y_iy_j\end{aligned} ∂zj∂yi=(j=1∑Cezj)2ezij=1∑Cezj−eziezj=j=1∑Cezjezi−j=1∑Cezjezij=1∑Cezjezj=yi−yiyj
当 i ≠ j i \not= j i=j 时:
∂ y i ∂ z j = 0 − e z i e z j ( ∑ j = 1 C e z j ) 2 = − y i y j \frac{\partial y_i}{\partial z_j} = \frac{0 - e^{z_i}e^{z_j}}{(\sum\limits_{j=1}^Ce^{z_j})^2} = -y_iy_j ∂zj∂yi=(j=1∑Cezj)20−eziezj=−yiyj
两者合并:
∂ y i ∂ z j = 1 { i = j } y i − y i y j \frac{\partial y_i}{\partial z_j} = \pmb{1}\{i=j\}y_i - y_iy_j ∂zj∂yi=111{i=j}yi−yiyj
其中 1 { i = j } = { 1 , i f i = j 0 , i f i ≠ j \pmb{1}\{i=j\} = \left\{\begin{aligned} & 1, \quad if \ \ i = j \\&0,\quad if \ \ i \not= j \end{aligned}\right. 111{i=j}={1,if i=j0,if i=j