CSP-S 2022题目与CSP-J 2022题目
CSP-J 2022洛谷自测：CSP-J 2022 自测 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
CSP-S 2022洛谷自测：CSP-S 2022 自测 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
P8816 [CSP-J 2022] 上升点列（民间数据）
# [CSP-J 2022] 上升点列（民间数据）
## 题目描述
在一个二维平面内，给定 $n$ 个整数点 $(x_i, y_i)$，此外你还可以自由添加 $k$ 个整数点。
你在自由添加 $k$ 个点后，还需要从 $n + k$ 个点中选出若干个整数点并组成一个序列，使得序列中任意相邻两点间的欧几里得距离恰好为 $1$ 而且横坐标、纵坐标值均单调不减，即 $x_{i+1} - x_i = 1, y_{i+1} = y_i$ 或 $y_{i+1} - y_i = 1, x_{i+1} = x_i$。请给出满足条件的序列的最大长度。
## 输入格式
第一行两个正整数 $n, k$ 分别表示给定的整点个数、可自由添加的整点个数。
接下来 $n$ 行，第 $i$ 行两个正整数 $x_i, y_i$ 表示给定的第 $i$ 个点的横纵坐标。
## 输出格式
输出一个整数表示满足要求的序列的最大长度。
## 样例 #1
### 样例输入 #1
```
8 2
3 1
3 2
3 3
3 6
1 2
2 2
5 5
5 3
```### 样例输出 #1
```
8
```## 样例 #2
### 样例输入 #2
```
4 100
10 10
15 25
20 20
30 30
```### 样例输出 #2
```
103
```## 提示
**【样例 \#3】**
见附件中的 `point/point3.in` 与 `point/point3.ans`。
第三个样例满足 $k = 0$。
**【样例 \#4】**
见附件中的 `point/point4.in` 与 `point/point4.ans`。
**【数据范围】**
保证对于所有数据满足：$1 \leq n \leq 500$，$0 \leq k \leq 100$。对于所有给定的整点，其横纵坐标 $1 \leq x_i, y_i \leq {10}^9$，且保证所有给定的点互不重合。对于自由添加的整点，其横纵坐标不受限制。
| 测试点编号 | $n \leq$ | $k \leq$ | $x_i,y_i \leq$ |
| :-----------: | :-----------: | :-----------: | :-----------: |
| $1 \sim 2$ | $10$ | $0$ | $10$ |
| $3 \sim 4$ | $10$ | $100$ | $100$ |
| $5 \sim 7$ | $500$ | $0$ | $100$ |
| $8 \sim 10$ | $500$ | $0$ | ${10}^9$ |
| $11 \sim 15$ | $500$ | $100$ | $100$ |
| $16 \sim 20$ | $500$ | $100$ | ${10}^9$ |P8815 [CSP-J 2022] 逻辑表达式（民间数据）
# [CSP-J 2022] 逻辑表达式（民间数据）
## 题目背景
由于本题情况多样，上传了两个 Subtask 对应两份不同的民间数据。Subtask 0 中强度较低，Subtask 1 中强度较高。分数是计算两个 Subtask 中最低分。
$\text{upd 2022.10.29 21:41}$：**Subtask 1** 已重新加强。
## 题目描述
逻辑表达式是计算机科学中的重要概念和工具，包含逻辑值、逻辑运算、逻辑运算优先级等内容。
在一个逻辑表达式中，元素的值只有两种可能：$0$（表示假）和 $1$（表示真）。元素之间有多种可能的逻辑运算，本题中只需考虑如下两种：“与”（符号为 `&`）和“或”（符号为 `|`）。其运算规则如下：
$0 \mathbin{\&} 0 = 0 \mathbin{\&} 1 = 1 \mathbin{\&} 0 = 0$，$1 \mathbin{\&} 1 = 1$；
$0 \mathbin{|} 0 = 0$，$0 \mathbin{|} 1 = 1 \mathbin{|} 0 = 1 \mathbin{|} 1 = 1$。在一个逻辑表达式中还可能有括号。规定在运算时，括号内的部分先运算；两种运算并列时，`&` 运算优先于 `|` 运算；同种运算并列时，从左向右运算。
比如，表达式 `0|1&0` 的运算顺序等同于 `0|(1&0)`；表达式 `0&1&0|1` 的运算顺序等同于 `((0&1)&0)|1`。
此外，在 C++ 等语言的有些编译器中，对逻辑表达式的计算会采用一种“短路”的策略：在形如 `a&b` 的逻辑表达式中，会先计算 `a` 部分的值，如果 $a = 0$，那么整个逻辑表达式的值就一定为 $0$，故无需再计算 `b` 部分的值；同理，在形如 `a|b` 的逻辑表达式中，会先计算 `a` 部分的值，如果 $a = 1$，那么整个逻辑表达式的值就一定为 $1$，无需再计算 `b` 部分的值。
现在给你一个逻辑表达式，你需要计算出它的值，并且统计出在计算过程中，两种类型的“短路”各出现了多少次。需要注意的是，如果某处“短路”包含在更外层被“短路”的部分内则不被统计，如表达式 `1|(0&1)` 中，尽管 `0&1` 是一处“短路”，但由于外层的 `1|(0&1)` 本身就是一处“短路”，无需再计算 `0&1` 部分的值，因此不应当把这里的 `0&1` 计入一处“短路”。
## 输入格式
输入共一行，一个非空字符串 $s$ 表示待计算的逻辑表达式。
## 输出格式
输出共两行，第一行输出一个字符 `0` 或 `1`，表示这个逻辑表达式的值；第二行输出两个非负整数，分别表示计算上述逻辑表达式的过程中，形如 `a&b` 和 `a|b` 的“短路”各出现了多少次。
## 样例 #1
### 样例输入 #1
```
0&(1|0)|(1|1|1&0)
```### 样例输出 #1
```
1
1 2
```## 样例 #2
### 样例输入 #2
```
(0|1&0|1|1|(1|1))&(0&1&(1|0)|0|1|0)&0
```### 样例输出 #2
```
0
2 3
```## 提示
**【样例解释 \#1】**
该逻辑表达式的计算过程如下，每一行的注释表示上一行计算的过程：
```plain
0&(1|0)|(1|1|1&0)
=(0&(1|0))|((1|1)|(1&0)) //用括号标明计算顺序
=0|((1|1)|(1&0)) //先计算最左侧的 &，是一次形如 a&b 的“短路”
=0|(1|(1&0)) //再计算中间的 |，是一次形如 a|b 的“短路”
=0|1 //再计算中间的 |，是一次形如 a|b 的“短路”
=1
```**【样例 \#3】**
见附件中的 `expr/expr3.in` 与 `expr/expr3.ans`。
**【样例 \#4】**
见附件中的 `expr/expr4.in` 与 `expr/expr4.ans`。
**【数据范围】**
设 $\lvert s \rvert$ 为字符串 $s$ 的长度。
对于所有数据，$1 \le \lvert s \rvert \le {10}^6$。保证 $s$ 中仅含有字符 `0`、`1`、`&`、`|`、`(`、`)` 且是一个符合规范的逻辑表达式。保证输入字符串的开头、中间和结尾均无额外的空格。保证 $s$
中没有重复的括号嵌套（即没有形如 `((a))` 形式的子串，其中 `a` 是符合规范的逻辑表
达式）。| 测试点编号 | $\lvert s \rvert \le$ | 特殊条件 |
|:-:|:-:|:-:|
| $1 \sim 2$ | $3$ | 无 |
| $3 \sim 4$ | $5$ | 无 |
| $5$ | $2000$ | 1 |
| $6$ | $2000$ | 2 |
| $7$ | $2000$ | 3 |
| $8 \sim 10$ | $2000$ | 无 |
| $11 \sim 12$ | ${10}^6$ | 1 |
| $13 \sim 14$ | ${10}^6$ | 2 |
| $15 \sim 17$ | ${10}^6$ | 3 |
| $18 \sim 20$ | ${10}^6$ | 无 |其中：
特殊性质 1 为：保证 $s$ 中没有字符 `&`。
特殊性质 2 为：保证 $s$ 中没有字符 `|`。
特殊性质 3 为：保证 $s$ 中没有字符 `(` 和 `)`。**【提示】**
以下给出一个“符合规范的逻辑表达式”的形式化定义：
- 字符串 `0` 和 `1` 是符合规范的；
- 如果字符串 `s` 是符合规范的，且 `s` 不是形如 `(t)` 的字符串（其中 `t` 是符合规范的），那么字符串 `(s)` 也是符合规范的；
- 如果字符串 `a` 和 `b` 均是符合规范的，那么字符串 `a&b`、`a|b` 均是符合规范的；
- 所有符合规范的逻辑表达式均可由以上方法生成。P8814 [CSP-J 2022] 解密（民间数据）
# [CSP-J 2022] 解密（民间数据）
## 题目描述
给定一个正整数 $k$，有 $k$ 次询问，每次给定三个正整数 $n_i, e_i, d_i$，求两个正整数 $p_i, q_i$，使 $n_i = p_i \times q_i$、$e_i \times d_i = (p_i - 1)(q_i - 1) + 1$。
## 输入格式
第一行一个正整数 $k$，表示有 $k$ 次询问。
接下来 $k$ 行，第 $i$ 行三个正整数 $n_i, d_i, e_i$。
## 输出格式
输出 $k$ 行，每行两个正整数 $p_i, q_i$ 表示答案。
为使输出统一，你应当保证 $p_i \leq q_i$。
如果无解，请输出 `NO`。
## 样例 #1
### 样例输入 #1
```
10
770 77 5
633 1 211
545 1 499
683 3 227
858 3 257
723 37 13
572 26 11
867 17 17
829 3 263
528 4 109
```### 样例输出 #1
```
2 385
NO
NO
NO
11 78
3 241
2 286
NO
NO
6 88
```## 提示
**【样例 \#2】**
见附件中的 `decode/decode2.in` 与 `decode/decode2.ans`。
**【样例 \#3】**
见附件中的 `decode/decode3.in` 与 `decode/decode3.ans`。
**【样例 \#4】**
见附件中的 `decode/decode4.in` 与 `decode/decode4.ans`。
**【数据范围】**
以下记 $m = n - e \times d + 2$。
保证对于 $100\%$ 的数据，$1 \leq k \leq {10}^5$，对于任意的 $1 \leq i \leq k$，$1 \leq n_i \leq {10}^{18}$，$1 \leq e_i \times d_i \leq {10}^{18}$
，$1 \leq m \leq {10}^9$。| 测试点编号 | $k \leq$ | $n \leq$ | $m \leq$ | 特殊性质 |
| :----------: | :----------: | :----------: | :----------: | :----------: |
| $1$ | $10^3$ | $10^3$ | $10^3$ | 保证有解 |
| $2$ | $10^3$ | $10^3$ | $10^3$ | 无 |
| $3$ | $10^3$ | $10^9$ | $6\times 10^4$ | 保证有解 |
| $4$ | $10^3$ | $10^9$ | $6\times 10^4$ | 无 |
| $5$ | $10^3$ | $10^9$ | $10^9$ | 保证有解 |
| $6$ | $10^3$ | $10^9$ | $10^9$ | 无 |
| $7$ | $10^5$ | $10^{18}$ | $10^9$ | 保证若有解则 $p=q$ |
| $8$ | $10^5$ | $10^{18}$ | $10^9$ | 保证有解 |
| $9$ | $10^5$ | $10^{18}$ | $10^9$ | 无 |
| $10$ | $10^5$ | $10^{18}$ | $10^9$ | 无 |P8813 [CSP-J 2022] 乘方（民间数据）
# [CSP-J 2022] 乘方（民间数据）
## 题目描述
小文同学刚刚接触了信息学竞赛，有一天她遇到了这样一个题：给定正整数 $a$ 和 $b$，求 $a^b$ 的值是多少。
$a^b$ 即 $b$ 个 $a$ 相乘的值，例如 $2^3$ 即为 $3$ 个 $2$ 相乘，结果为 $2 \times 2 \times 2 = 8$。
“简单！”小文心想，同时很快就写出了一份程序，可是测试时却出现了错误。
小文很快意识到，她的程序里的变量都是 `int` 类型的。在大多数机器上，`int` 类型能表示的最大数为 $2^{31} - 1$，因此只要计算结果超过这个数，她的程序就会出现错误。
由于小文刚刚学会编程，她担心使用 `int` 计算会出现问题。因此她希望你在 $a^b$ 的值超过 ${10}^9$ 时，输出一个 `-1` 进行警示，否则就输出正确的 $a^b$ 的值。
然而小文还是不知道怎么实现这份程序，因此她想请你帮忙。
## 输入格式
输入共一行，两个正整数 $a, b$。
## 输出格式
输出共一行，如果 $a^b$ 的值不超过 ${10}^9$，则输出 $a^b$ 的值，否则输出 `-1`。
## 样例 #1
### 样例输入 #1
```
10 9
```### 样例输出 #1
```
1000000000
```## 样例 #2
### 样例输入 #2
```
23333 66666
```### 样例输出 #2
```
-1
```## 提示
对于 $10 \%$ 的数据，保证 $b = 1$。
对于 $30 \%$ 的数据，保证 $b \le 2$。
对于 $60 \%$ 的数据，保证 $b \le 30$，$a^b \le {10}^{18}$。
对于 $100 \%$ 的数据，保证 $1 \le a, b \le {10}^9$。P8820 [CSP-S 2022] 数据传输（民间数据）
# [CSP-S 2022] 数据传输（民间数据）
## 题目背景
## 请勿滥用本题评测，后果自负。
## 题目描述
小 C 正在设计计算机网络中的路由系统。
测试用的网络总共有 $n$ 台主机，依次编号为 $1 \sim n$。这 $n$ 台主机之间由 $n - 1$ 根网线连接，第 $i$ 条网线连接个主机 $a_i$ 和 $b_i$。保证任意两台主机可以通过有限根网线直接或者间接地相连。受制于信息发送的功率，主机 $a$ 能够直接将信息传输给主机 $b$ 当且仅当两个主机在可以通过不超过 $k$ 根网线直接或者间接的相连。
在计算机网络中，数据的传输往往需要通过若干次转发。假定小 C 需要将数据从主机 $a$ 传输到主机 $b$（$a \neq b$），则其会选择出若干台用于传输的主机 $c_1 = a, c_2, \ldots, c_{m - 1}, c_m = b$，并按照如下规则转发：对于所有的 $1 \le i < m$，主机 $c_i$ 将信息直接发送给 $c_{i + 1}$。
每台主机处理信息都需要一定的时间，第 $i$ 台主机处理信息需要 $v_i$ 单位的时间。数据在网络中的传输非常迅速，因此传输的时间可以忽略不计。据此，上述传输过程花费的时间为 $\sum_{i = 1}^{m} v_{c_i}$。
现在总共有 $q$ 次数据发送请求，第 $i$ 次请求会从主机 $s_i$ 发送数据到主机 $t_i$。小 C 想要知道，对于每一次请求至少需要花费多少单位时间才能完成传输。
## 输入格式
输入的第一行包含三个正整数 $n, Q, k$，分别表示网络主机个数，请求个数，传输参数。数据保证 $1 \le n \le 2 \times {10}^5$，$1 \le Q \le 2 \times {10}^5$，$1 \le k \le 3$。
输入的第二行包含 $n$ 个正整数，第 $i$ 个正整数表示 $v_i$，保证 $1 \le v_i \le {10}^9$。
接下来 $n - 1$ 行，第 $i$ 行包含两个正整数 $a_i, b_i$，表示一条连接主机 $a_i, b_i$ 的网线。保证 $1 \le a_i, b_i \le n$。
接下来 $Q$ 行，第 $i$ 行包含两个正整数 $s_i, t_i$，表示一次从主机 $s_i$ 发送数据到主机 $t_i$ 的请求。保证 $1 \le s_i, t_i \le n$，$s_i \ne t_i$。
## 输出格式
$Q$ 行，每行一个正整数，表示第 $i$ 次请求在传输的时候至少需要花费多少单位的时间。
## 样例 #1
### 样例输入 #1
```
7 3 3
1 2 3 4 5 6 7
1 2
1 3
2 4
2 5
3 6
3 7
4 7
5 6
1 2
```### 样例输出 #1
```
12
12
3
```## 提示
**【样例解释 \#1】**
对于第一组请求，由于主机 $4, 7$ 之间需要至少 $4$ 根网线才能连接，因此数据无法在两台主机之间直接传输，其至少需要一次转发；我们让其在主机 $1$ 进行一次转发，不难发现主机 $1$ 和主机 $4, 7$ 之间都只需要两根网线即可连接，且主机 $1$ 的数据处理时间仅为 $1$，为所有主机中最小，因此最少传输的时间为 $4 + 1 + 7 = 12$。
对于第三组请求，由于主机 $1, 2$ 之间只需要 $1$ 根网线就能连接，因此数据直接传输就是最优解，最少传输的时间为 $1 + 2 = 3$。
**【样例 \#2】**
见附件中的 `transmit/transmit2.in` 与 `transmit/transmit2.ans`。
该样例满足测试点 $2$ 的限制。
**【样例 \#3】**
见附件中的 `transmit/transmit3.in` 与 `transmit/transmit3.ans`。
该样例满足测试点 $3$ 的限制。
**【样例 \#4】**
见附件中的 `transmit/transmit4.in` 与 `transmit/transmit4.ans`。
该样例满足测试点 $20$ 的限制。
**【数据范围】**
对于所有的测试数据，满足 $1 \le n \le 2 \times {10}^5$，$1 \le Q \le 2 \times {10}^5$，$1 \le k \le 3$，$1 \le a_i, b_i \le n$，$1 \le s_i, t_i \le n$，$s_i \ne t_i$。
| 测试点 | $n \le$ | $Q \le$ | $k =$ | 特殊性质 |
|:-:|:-:|:-:|:-:|:-:|
| $1$ | $10$ | $10$ | $2$ | 是 |
| $2$ | $10$ | $10$ | $3$ | 是 |
| $3$ | $200$ | $200$ | $2$ | 是 |
| $4 \sim 5$ | $200$ | $200$ | $3$ | 是 |
| $6 \sim 7$ | $2000$ | $2000$ | $1$ | 否 |
| $8 \sim 9$ | $2000$ | $2000$ | $2$ | 否 |
| $10 \sim 11$ | $2000$ | $2000$ | $3$ | 否 |
| $12 \sim 13$ | $2 \times {10}^5$ | $2 \times {10}^5$ | $1$ | 否 |
| $14$ | $5 \times {10}^4$ | $5 \times {10}^4$ | $2$ | 是 |
| $15 \sim 16$ | ${10}^5$ | ${10}^5$ | $2$ | 是 |
| $17 \sim 19$ | $2 \times {10}^5$ | $2 \times {10}^5$ | $2$ | 否 |
| $20$ | $5 \times {10}^4$ | $5 \times {10}^4$ | $3$ | 是 |
| $21 \sim 22$ | ${10}^5$ | ${10}^5$ | $3$ | 是 |
| $23 \sim 25$ | $2 \times {10}^5$ | $2 \times {10}^5$ | $3$ | 否 |特殊性质：保证 $a_i = i + 1$，而 $b_i$ 则从 $1, 2, \ldots, i$ 中等概率选取。
P8820 [CSP-S 2022] 数据传输（民间数据）
# [CSP-S 2022] 数据传输（民间数据）
## 题目背景
## 请勿滥用本题评测，后果自负。
## 题目描述
小 C 正在设计计算机网络中的路由系统。
测试用的网络总共有 $n$ 台主机，依次编号为 $1 \sim n$。这 $n$ 台主机之间由 $n - 1$ 根网线连接，第 $i$ 条网线连接个主机 $a_i$ 和 $b_i$。保证任意两台主机可以通过有限根网线直接或者间接地相连。受制于信息发送的功率，主机 $a$ 能够直接将信息传输给主机 $b$ 当且仅当两个主机在可以通过不超过 $k$ 根网线直接或者间接的相连。
在计算机网络中，数据的传输往往需要通过若干次转发。假定小 C 需要将数据从主机 $a$ 传输到主机 $b$（$a \neq b$），则其会选择出若干台用于传输的主机 $c_1 = a, c_2, \ldots, c_{m - 1}, c_m = b$，并按照如下规则转发：对于所有的 $1 \le i < m$，主机 $c_i$ 将信息直接发送给 $c_{i + 1}$。
每台主机处理信息都需要一定的时间，第 $i$ 台主机处理信息需要 $v_i$ 单位的时间。数据在网络中的传输非常迅速，因此传输的时间可以忽略不计。据此，上述传输过程花费的时间为 $\sum_{i = 1}^{m} v_{c_i}$。
现在总共有 $q$ 次数据发送请求，第 $i$ 次请求会从主机 $s_i$ 发送数据到主机 $t_i$。小 C 想要知道，对于每一次请求至少需要花费多少单位时间才能完成传输。
## 输入格式
输入的第一行包含三个正整数 $n, Q, k$，分别表示网络主机个数，请求个数，传输参数。数据保证 $1 \le n \le 2 \times {10}^5$，$1 \le Q \le 2 \times {10}^5$，$1 \le k \le 3$。
输入的第二行包含 $n$ 个正整数，第 $i$ 个正整数表示 $v_i$，保证 $1 \le v_i \le {10}^9$。
接下来 $n - 1$ 行，第 $i$ 行包含两个正整数 $a_i, b_i$，表示一条连接主机 $a_i, b_i$ 的网线。保证 $1 \le a_i, b_i \le n$。
接下来 $Q$ 行，第 $i$ 行包含两个正整数 $s_i, t_i$，表示一次从主机 $s_i$ 发送数据到主机 $t_i$ 的请求。保证 $1 \le s_i, t_i \le n$，$s_i \ne t_i$。
## 输出格式
$Q$ 行，每行一个正整数，表示第 $i$ 次请求在传输的时候至少需要花费多少单位的时间。
## 样例 #1
### 样例输入 #1
```
7 3 3
1 2 3 4 5 6 7
1 2
1 3
2 4
2 5
3 6
3 7
4 7
5 6
1 2
```### 样例输出 #1
```
12
12
3
```## 提示
**【样例解释 \#1】**
对于第一组请求，由于主机 $4, 7$ 之间需要至少 $4$ 根网线才能连接，因此数据无法在两台主机之间直接传输，其至少需要一次转发；我们让其在主机 $1$ 进行一次转发，不难发现主机 $1$ 和主机 $4, 7$ 之间都只需要两根网线即可连接，且主机 $1$ 的数据处理时间仅为 $1$，为所有主机中最小，因此最少传输的时间为 $4 + 1 + 7 = 12$。
对于第三组请求，由于主机 $1, 2$ 之间只需要 $1$ 根网线就能连接，因此数据直接传输就是最优解，最少传输的时间为 $1 + 2 = 3$。
**【样例 \#2】**
见附件中的 `transmit/transmit2.in` 与 `transmit/transmit2.ans`。
该样例满足测试点 $2$ 的限制。
**【样例 \#3】**
见附件中的 `transmit/transmit3.in` 与 `transmit/transmit3.ans`。
该样例满足测试点 $3$ 的限制。
**【样例 \#4】**
见附件中的 `transmit/transmit4.in` 与 `transmit/transmit4.ans`。
该样例满足测试点 $20$ 的限制。
**【数据范围】**
对于所有的测试数据，满足 $1 \le n \le 2 \times {10}^5$，$1 \le Q \le 2 \times {10}^5$，$1 \le k \le 3$，$1 \le a_i, b_i \le n$，$1 \le s_i, t_i \le n$，$s_i \ne t_i$。
| 测试点 | $n \le$ | $Q \le$ | $k =$ | 特殊性质 |
|:-:|:-:|:-:|:-:|:-:|
| $1$ | $10$ | $10$ | $2$ | 是 |
| $2$ | $10$ | $10$ | $3$ | 是 |
| $3$ | $200$ | $200$ | $2$ | 是 |
| $4 \sim 5$ | $200$ | $200$ | $3$ | 是 |
| $6 \sim 7$ | $2000$ | $2000$ | $1$ | 否 |
| $8 \sim 9$ | $2000$ | $2000$ | $2$ | 否 |
| $10 \sim 11$ | $2000$ | $2000$ | $3$ | 否 |
| $12 \sim 13$ | $2 \times {10}^5$ | $2 \times {10}^5$ | $1$ | 否 |
| $14$ | $5 \times {10}^4$ | $5 \times {10}^4$ | $2$ | 是 |
| $15 \sim 16$ | ${10}^5$ | ${10}^5$ | $2$ | 是 |
| $17 \sim 19$ | $2 \times {10}^5$ | $2 \times {10}^5$ | $2$ | 否 |
| $20$ | $5 \times {10}^4$ | $5 \times {10}^4$ | $3$ | 是 |
| $21 \sim 22$ | ${10}^5$ | ${10}^5$ | $3$ | 是 |
| $23 \sim 25$ | $2 \times {10}^5$ | $2 \times {10}^5$ | $3$ | 否 |特殊性质：保证 $a_i = i + 1$，而 $b_i$ 则从 $1, 2, \ldots, i$ 中等概率选取。
P8819 [CSP-S 2022] 星战（暂无数据）
# [CSP-S 2022] 星战（暂无数据）
## 题目背景
# 本题暂不支持评测，请不要提交
# 本题暂不支持评测，请不要提交
# 本题暂不支持评测，请不要提交
# 本题暂不支持评测，请不要提交
# 本题暂不支持评测，请不要提交
# 本题暂不支持评测，请不要提交
# 本题暂不支持评测，请不要提交
# 本题暂不支持评测，请不要提交
## 题目描述
在这一轮的星际战争中，我方在宇宙中建立了 $n$ 个据点，以 $m$ 个单向虫洞连接。我们把终点为据点 $u$ 的所有虫洞归为据点 $u$ 的虫洞。
战火纷飞之中这些虫洞很难长久存在，敌人的打击随时可能到来。这些打击中的有效打击可以分为两类：
1. 敌人会摧毁某个虫洞，这会使它连接的两个据点无法再通过这个虫洞直接到达，但这样的打击无法摧毁它连接的两个据点。
2. 敌人会摧毁某个据点，由于虫洞的主要技术集中在出口处，这会导致该据点的所有还未被摧毁的虫洞被一同摧毁。而从这个据点出发的虫洞则**不会摧毁**。注意：摧毁只会导致虫洞不可用，而不会消除它的存在。
为了抗击敌人并维护各部队和各据点之间的联系，我方发展出了两种特种部队负责修复虫洞：
- A 型特种部队则可以将某个特定的虫洞修复。
- B 型特种部队可以将某据点的所有损坏的虫洞修复。考虑到敌人打击的特点，我方并未在据点上储备过多的战略物资。因此只要这个据点的某一条虫洞被修复，处于可用状态，那么这个据点也是可用的。
我方掌握了一种苛刻的空间特性，利用这一特性我方战舰可以沿着虫洞瞬移到敌方阵营，实现精确打击。
为了把握发动反攻的最佳时机，指挥部必须关注战场上的所有变化，为了寻找一个能够进行反攻的时刻。总指挥认为：
- 如果从我方的任何据点出发，在选择了合适的路线的前提下，可以进行无限次的虫洞穿梭（可以多次经过同一据点或同一虫洞），那么这个据点就可以**实现反击**。
- 为了使虫洞穿梭的过程连续，尽量减少战舰在据点切换虫洞时的质能损耗，当且仅当**只有一个从该据点出发的虫洞可用**时，这个据点可以**实现连续穿梭**。
- 如果我方所有据点都可以**实现反击**，也都可以**实现连续穿梭**，那么这个时刻就是一个绝佳的**反攻**时刻。总司令为你下达命令，要求你根据战场上实时反馈的信息，迅速告诉他当前的时刻是否能够进行一次**反攻**。
## 输入格式
输入的第一行包含两个正整数 $n,m$。
接下来 $m$ 行每行两个数 $u,v$，表示一个从据点 $u$ 出发到据点 $v$ 的虫洞。保证 $u \ne v$，保证不会有两条相同的虫洞。初始时所有的虫洞和据点都是完好的。
接下来一行一个正整数 $q$ 表示询问个数。
接下来 $q$ 行每行表示一次询问或操作。首先读入一个正整数 $t$ 表示指令类型：
- 若 $t = 1$，接下来两个整数 $u, v$ 表示敌人摧毁了从据点 $u$ 出发到据点 $v$ 的虫洞。保证该虫洞存在且未被摧毁。
- 若 $t = 2$，接下来一个整数 $u$ 表示敌人摧毁了据点 $u$。如果该据点的虫洞已全部 被摧毁，那么这次袭击不会有任何效果。
- 若 $t = 3$，接下来两个整数 $u, v$ 表示我方修复了从据点 $u$ 出发到据点 $v$ 的虫洞。保证该虫洞存在且被摧毁。
- 若 $t = 4$，接下来一个整数 $u$ 表示我方修复了据点 $u$。如果该据点没有被摧毁的虫洞，那么这次修复不会有任何效果。在每次指令执行之后，你需要判断能否进行一次反攻。如果能则输出 `YES` 否则输出 `NO`。
## 输出格式
输出一共 $q$ 行。对于每个指令，输出这个指令执行后能否进行反攻。
## 样例 #1
### 样例输入 #1
```
3 6
2 3
2 1
1 2
1 3
3 1
3 2
11
1 3 2
1 2 3
1 1 3
1 1 2
3 1 3
3 3 2
2 3
1 3 1
3 1 3
4 2
1 3 2
```### 样例输出 #1
```
NO
NO
YES
NO
YES
NO
NO
NO
YES
NO
NO
```## 提示
**【样例解释 \#1】**
虫洞状态可以参考下面的图片, 图中的边表示存在且未被摧毁的虫洞：
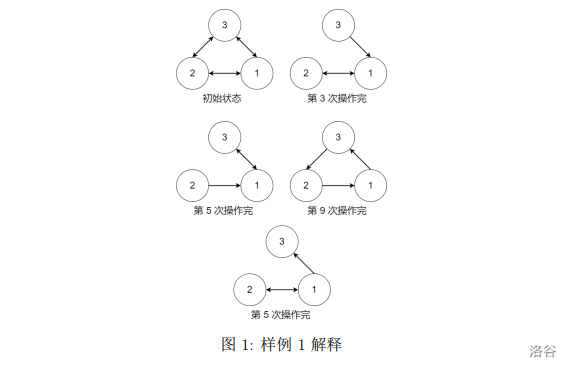
**【样例 \#2】**
见附件中的 `galaxy/galaxy2.in` 与 `galaxy/galaxy2.ans`。
**【样例 \#3】**
见附件中的 `galaxy/galaxy3.in` 与 `galaxy/galaxy3.ans`。
**【样例 \#4】**
见附件中的 `galaxy/galaxy4.in` 与 `galaxy/galaxy4.ans`。
**【数据范围】**
对于所有数据保证：$1 \le n \le 5 \times {10}^5$，$1 \le m \le 5 \times {10}^5$，$1 \le q \le 5 \times {10}^5$。
| 测试点 | $n \le$ | $m \le$ | $q \le$ | 特殊限制 |
| :-----------: | :-----------: | :-----------: | :-----------: | :-----------: |
| $1 \sim 3$ | $10$ | $20$ | $50$ | 无 |
| $4 \sim 8$ | ${10}^3$ | ${10}^4$ | ${10}^3$ | 无 |
| $9 \sim 10$ | $5 \times {10}^5$ | $5 \times {10}^5$ | $5 \times {10}^5$ | 保证没有 $t = 2$ 和 $t = 4$ 的情况 |
| $11 \sim 12$ | $5 \times {10}^5$ | $5 \times {10}^5$ | $5 \times {10}^5$ | 保证没有 $t = 4$ 的情况 |
| $13 \sim 16$ | ${10}^5$ | $5 \times {10}^5$ | $5 \times {10}^5$ | 无 |
| $17 \sim 20$ | $5 \times {10}^5$ | $5\times 10^5$ | $5 \times {10}^5$ | 无 |P8818 [CSP-S 2022] 策略游戏（民间数据）
# [CSP-S 2022] 策略游戏（民间数据）
## 题目描述
小 L 和小 Q 在玩一个策略游戏。
有一个长度为 $n$ 的数组 $A$ 和一个长度为 $m$ 的数组 $B$，在此基础上定义一个大小为 $n \times m$ 的矩阵 $C$，满足 $C_{i j} = A_i \times B_j$。所有下标均从 $1$ 开始。
游戏一共会进行 $q$ 轮，在每一轮游戏中，会事先给出 $4$ 个参数 $l_1, r_1, l_2, r_2$，满足 $1 \le l_1 \le r_1 \le n$、$1 \le l_2 \le r_2 \le m$。
游戏中，小 L 先选择一个 $l_1 \sim r_1$ 之间的下标 $x$，然后小 Q 选择一个 $l_2 \sim r_2$ 之间的下标 $y$。定义这一轮游戏中二人的得分是 $C_{x y}$。
小 L 的目标是使得这个得分尽可能大，小 Q 的目标是使得这个得分尽可能小。同时两人都是足够聪明的玩家，每次都会采用最优的策略。
请问：按照二人的最优策略，每轮游戏的得分分别是多少？
## 输入格式
第一行输入三个正整数 $n, m, q$，分别表示数组 $A$，数组 $B$ 的长度和游戏轮数。
第二行：$n$ 个整数，表示 $A_i$，分别表示数组 $A$ 的元素。
第三行：$m$ 个整数，表示 $B_i$，分别表示数组 $B$ 的元素。
接下来 $q$ 行，每行四个正整数，表示这一次游戏的 $l_1, r_1, l_2, r_2$。
## 输出格式
输出共 $q$ 行，每行一个整数，分别表示每一轮游戏中，小 L 和小 Q 在最优策略下的得分。
## 样例 #1
### 样例输入 #1
```
3 2 2
0 1 -2
-3 4
1 3 1 2
2 3 2 2
```### 样例输出 #1
```
0
4
```## 样例 #2
### 样例输入 #2
```
6 4 5
3 -1 -2 1 2 0
1 2 -1 -3
1 6 1 4
1 5 1 4
1 4 1 2
2 6 3 4
2 5 2 3
```### 样例输出 #2
```
0
-2
3
2
-1
```## 提示
**【样例解释 \#1】**
这组数据中，矩阵 $C$ 如下：
$$ \begin{bmatrix} 0 & 0 \\ -3 & 4 \\ 6 & -8 \end{bmatrix} $$
在第一轮游戏中，无论小 L 选取的是 $x = 2$ 还是 $x = 3$，小 Q 都有办法选择某个 $y$ 使得最终的得分为负数。因此小 L 选择 $x = 1$ 是最优的，因为这样得分一定为 $0$。
而在第二轮游戏中，由于小 L 可以选 $x = 2$，小 Q 只能选 $y = 2$，如此得分为 $4$。
**【样例 \#3】**
见附件中的 `game/game3.in` 与 `game/game3.ans`。
**【样例 \#4】**
见附件中的 `game/game4.in` 与 `game/game4.ans`。
**【数据范围】**
对于所有数据，$1 \le n, m, q \le {10}^5$，$-{10}^9 \le A_i, B_i \le {10}^9$。对于每轮游戏而言，$1 \le l_1 \le r_1 \le n$，$1 \le l_2 \le r_2 \le m$。
| 测试点编号 | $n, m, q \le$ | 特殊条件 |
|:-:|:-:|:-:|
| $1$ | $200$ | 1, 2 |
| $2$ | $200$ | 1 |
| $3$ | $200$ | 2 |
| $4 \sim 5$ | $200$ | 无 |
| $6$ | $1000$ | 1, 2 |
| $7 \sim 8$ | $1000$ | 1 |
| $9 \sim 10$ | $1000$ | 2 |
| $11 \sim 12$ | $1000$ | 无 |
| $13$ | ${10}^5$ | 1, 2 |
| $14 \sim 15$ | ${10}^5$ | 1 |
| $16 \sim 17$ | ${10}^5$ | 2 |
| $18 \sim 20$ | ${10}^5$ | 无 |其中，特殊性质 1 为：保证 $A_i, B_i > 0$。
特殊性质 2 为：保证对于每轮游戏而言，要么 $l_1 = r_1$，要么 $l_2 = r_2$。资源：
P8816 [CSP-J 2022] 上升点列（民间数据）https://www.luogu.com.cn/fe/api/problem/downloadAttachment/2lv8ponh?contestId=90215
https://www.luogu.com.cn/fe/api/problem/downloadAttachment/2lv8ponh?contestId=90215P8815 [CSP-J 2022] 逻辑表达式（民间数据）
https://www.luogu.com.cn/fe/api/problem/downloadAttachment/k8qm1nv3?contestId=90215
https://www.luogu.com.cn/fe/api/problem/downloadAttachment/k8qm1nv3?contestId=90215
https://www.luogu.com.cn/fe/api/problem/downloadAttachment/bsk6a00c?contestId=90215
https://www.luogu.com.cn/fe/api/problem/downloadAttachment/crnsxe4t?contestId=90216
P8818 [CSP-S 2022] 策略游戏（民间数据）：
https://www.luogu.com.cn/fe/api/problem/downloadAttachment/jfsjy9kj?contestId=90216
https://www.luogu.com.cn/fe/api/problem/downloadAttachment/jfsjy9kj?contestId=90216
思路：
假期计划（holiday）
首先进行 nn 次 BFS 预处理出 dist(i,j)dist(i,j)，表示两两之间的最少中转点个数（最短路）。
直觉告诉我们应该枚举 B,CB,C。那么 B−CB−C 能不能 kk 步到达直接利用 dist(B,C)≤kdist(B,C)≤k 来判断即可。接下来考虑对于已经确定的 B,CB,C，应该如何选择合理的 A,DA,D。
(A,B)(A,B) 和 (D,C)(D,C) 应该是完全等价的，这里不妨考虑前者。如果不考虑“点不重复”的限制，那么 AA 应该是所有满足 dist(1,A)≤kdist(1,A)≤k 且 dist(A,B)≤kdist(A,B)≤k 的点中权值最大的。预处理这个最优的决策点为 A1[B]A1[B]。同理预处理出次优点、次次优点，分别记为 A2[B]A2[B]、A3[B]A3[B]。
那么，在枚举 B,CB,C 之后，调用 Ai[B]Ai[B] 和 Di[C]Di[C]，判断合法性（是否重复）并计算权值最大的方案即可。
最短路、预处理、计算答案的时间复杂度均为 O(n2)O(n2)。
策略游戏（game）
首先分析当先手已经把 AiAi 选定时，后手应该怎么选择 BjBj 去使得答案最小：
- 能取异号的，那必然选异号的，而且要取绝对值最大的那个；
- 没有异号的，考虑取 00；
- 如果只能取同号的，那么一定取绝对值最小的那个。
总结一下以上几条策略，发现需要用到的量包括：区间内「负数」「正数」的“最大”和“最小”值以及「00」。在这样的情形下，考虑先手应该如何应对，不难发现，先手要取的数也必然是以上几种之一。
因此，使用线段树 / ST 表维护区间的以上几种信息。对于一次询问，先查询到 A[l1,r1]A[l1,r1] 和 B[l2,r2]B[l2,r2] 的这 5 个信息后，依次枚举先手决策、后手决策，对每个先手决策取最小值的最大值即是答案。
时间复杂度 O(nlogn)O(nlogn)。
星战（galaxy）
先把题面要求的东西翻译成人话：有一些删边、加边操作，查询是不是每个点的出度都恰好为 11（因为如果每个点都有出度的话，必然可以永远地走下去）。
既然如此，考虑维护每个点的出度。设集合 SS 表示目前存在的所有边的起点构成的可重集，那么，答案是 YES 当且仅当 S={1,2,⋯,n}S={1,2,⋯,n}。这里只需要判断集合是否相等，可以采用维护哈希值的方法，比如维护集合内元素的一次方和、二次方和、异或和之类的，看看两边是不是相同。
问题转化为了，在题目给定的加边、删边的条件下，动态维护 SS 的一些哈希值 HH。对于只有单点加、删，可以直接对哈希值 HH 进行修改。对于带有加、删以一个点 ii 为终点的所有边的时候情形稍复杂，可以预处理 UiUi 表示 ii 的所有入边对应起点的哈希值（比如一次方和、二次方和、异或和），动态维护 CiCi 表示当前时刻 ii 存在的所有入边对应起点的哈希值，以此来辅助更新。比如 HH 如果设定为一次方和，那么此时对 vv 进行第四类修复即可以表示为 H←H+(Uv−Cv)H←H+(Uv−Cv)、Cv←UvCv←Uv。其他同理。
时间复杂度 O(n)O(n)。
数据传输（transmit）
k=1k=1 的时候直接退化为求带权距离，再一来这是个静态问题，这启发我们使用树上倍增。
对于 k=2k=2，考虑求 s,ts,t 的答案的时候，把 s,ts,t 之间的链按顺序写下来，记作 u1=s,u2,u3,⋯,um=tu1=s,u2,u3,⋯,um=t，答案就应该是，选定其中的若干项，相邻两项之间的下标差不超过 22，然后求对应权值和的最小值。暴力做法可以是 dp，比如 fifi 表示最后一个当前落在 ii，最小权值和，转移的时候往前枚举至多两项（fi−1,fi−2fi−1,fi−2）来更新即可。
现在魔改这个东西变成树上倍增，用 f(u,p,i,j)f(u,p,i,j)（0≤i,j
而对于 k=3k=3，上述做法可能会出现问题，具体表现为可以“折返”：
其实这个问题通过改变 ff 的初始化方式就可以解决。除了初始化 f(u,0,0,1)f(u,0,0,1) 为 vuvu 之外，我们还额外地初始化 f(u,0,t,t+1)f(u,0,t,t+1)（t
时间复杂度 O(nk4logn)O(nk4logn)，感觉有点卡？