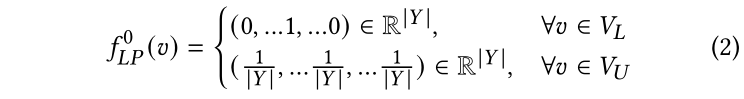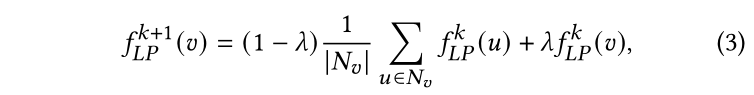【WWW2021】图神经网络的知识提取与超越:一个有效的知识蒸馏框架
点击上方,选择星标,每天给你送干货!
论文解读者:北邮 GAMMA Lab 博士生 刘佳玮
题目: Extract the Knowledge of Graph Neural Networks and Go Beyond it: An Effective Knowledge Distillation Framework
会议: WWW 2021
论文链接:
https://arxiv.org/pdf/2103.02885.pdf
论文代码:
https://github.com/BUPT-GAMMA/CPF
1 引言
随着深度学习的成功,基于图神经网络(GNN)的方法[8,12,30]已经证明了它们在分类节点标签方面的有效性。大多数GNN模型采用消息传递策略[7]:每个节点从其邻域聚合特征,然后将具有非线性激活的分层映射函数应用于聚合信息。这样,GNN可以在其模型中利用图结构和节点特征信息。
然而,这些神经模型的预测缺乏透明性,人们难以理解[36],而这对于与安全和道德相关的关键决策应用至关重要[5]。此外,图拓扑、节点特征和映射矩阵的耦合导致复杂的预测机制,无法充分利用数据中的先验知识。例如,已有研究表明,标签传播法采用上述同质性假设来表示的基于结构的先验,在图卷积网络(GCN)[12]中没有充分使用[15,31]。
作为证据,最近的研究提出通过添加正则化[31]或操纵图过滤器[15,25]将标签传播机制纳入GCN。他们的实验结果表明,通过强调这种基于结构的先验知识可以改善GCN。然而,这些方法具有三个主要缺点:(1)其模型的主体仍然是GNN,并阻止它们进行更可解释的预测;(2)它们是单一模型而不是框架,因此与其他高级GNN架构不兼容;(3)他们忽略了另一个重要的先验知识,即基于特征的先验知识,这意味着节点的标签完全由其自身的特征确定。
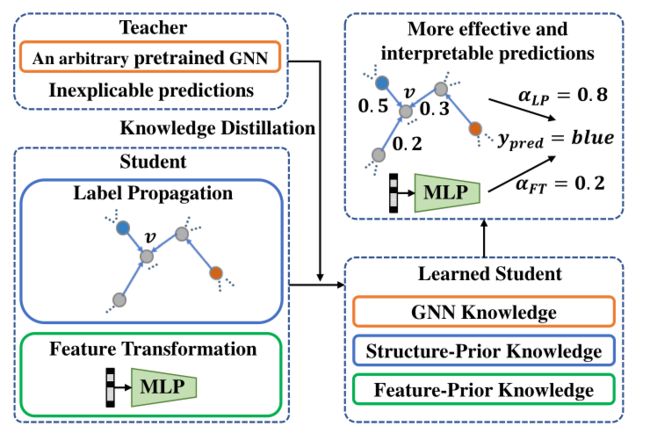
为了解决这些问题,我们提出了一个有效的知识蒸馏框架,以将任意预训练的GNN教师模型的知识注入精心设计的学生模型中。学生模型是通过两个简单的预测机制构建的,即标签传播和特征转换,它们自然分别保留了基于结构和基于特征的先验知识。具体来说,我们将学生模型设计为参数化标签传播和基于特征的2层感知机(MLP)的可训练组合。另一方面,已有研究表明,教师模型的知识在于其软预测[9]。通过模拟教师模型预测的软标签,我们的学生模型能够进一步利用预训练的GNN中的知识。因此,学习的学生模型具有更可解释的预测过程,并且可以利用GNN和基于结构/特征的先验知识。我们的框架概述如图1所示。
图1:我们的知识蒸馏框架的示意图。学生模型的两种简单预测机制可确保充分利用基于结构/功能的先验知识。在知识蒸馏过程中,将提取GNN教师中的知识并将其注入学生。因此,学生可以超越其相应的老师,得到更有效和可解释的预测。
我们在五个公共基准数据集上进行了实验,并采用了几种流行的GNN模型,包括GCN[12]、GAT[30]、SAGE[8]、APPNP[13]、SGC[33]和最新的深层GCN模型GCNII[4]作为教师模型。实验结果表明,就分类精度而言,学生模型的表现优于其相应的教师模型1.4%-4.7%。值得注意的是,我们也将框架应用于GLP[15],它通过操纵图过滤器来统一GCN和标签传播。结果,我们仍然可以获得1.5%-2.3%的相对改进,这表明了我们框架的潜在兼容性。此外,我们通过探究参数化标签传播与特征转换之间的可学习平衡参数以及标签传播中每个节点的可学习置信度得分,来研究学生模型的可解释性。总而言之,改进是一致,并且更重要的是,它具有更好的可解释性。
本文的贡献总结如下:
我们提出了一个有效的知识蒸馏框架,以提取任意预训练的GNN模型的知识,并将其注入学生模型,以实现更有效和可解释的预测。
我们将学生模型设计为参数化标签传播和基于特征的两层MLP的可训练组合。因此,学生模型有一个更可解释的预测过程,并自然地保留了基于结构/特征的先验。因此,学习的学生模型可以同时利用GNN和先验知识。
五个基准数据集和七个GNN教师模型上的实验结果表明了我们的框架有效性。对学生模型中学习权重的广泛研究也说明了我们方法的可解释性。
2 方法
在本节中,我们将从形式化半监督节点分类问题开始,并介绍符号。然后,我们将展示我们的知识蒸馏框架,以提取GNN的知识。然后,我们将提出学生模型的体系结构,该模型是参数化标签传播和基于特征的两层MLP的可训练组合。最后,我们将讨论学生模型的可解释性和框架的计算复杂性。
2.1 半监督节点分类
我们首先概述节点分类问题。给定一个连通图 和一个标记点集 ,其中 师节点集, 是边集,节点分类的目标是为每个节点无标记点集 中的节点 预测标签。每个节点 拥有标签 ,其中 是所有可能的标签集合。此外,图数据通常拥有节点特征 ,并且可以利用特征来提升分类准确率。每行矩阵 的每行 表示节点 的 维特征向量。
2.2 知识蒸馏框架
基于GNN的节点分类方法往往是一个黑盒,输入图结构 、标记点集 和节点特征 ,输出分类器 。分类器 将预测无标记点 的标签为 的概率 ,其中 。对于标记节点 ,如果 的标签为 ,那么 ,其余标签 。简化起见,我们使用 表示所有标签的概率分布。
在本文中,我们框架里的教师模型可以使用任意GNN,例如GCN[12]或GAT[30]。我们称教师模型里的预训练分类器为 。另一方面,我们使用 表示学生模型, 是参数, 表示学生模型对节点v的预测概率分布。
在知识蒸馏[9]的框架中,训练学生模型使其最小化与预训练教师模型的软标签预测,使得教师模型里的潜在知识被提取并注入学生模型中。因此,优化目标是对齐学生模型和与训练教师模型的输出,可以形式化为:
其中 度量两个预测概率分布之间的距离。特别地,本文使用欧氏距离。(注:我们还尝试最小化KL散度或最大化交叉熵。但是我们发现欧几里得距离的效果最好,并且在数值上更稳定。)
2.3 学生模型架构
我们假设节点的标签预测遵循两种简单的机制:(1)从其相邻节点传播标签;(2)从其自身特征进行转换。因此,如图2所示,我们将学生模型设计为这两种机制的组合,即参数化标签传播(PLP)模块和特征转换(FT)模块,它们可以自然地分别保留基于结构的先验知识和基于特征的先验知识。蒸馏后,学生将通过更易于解释的预测机制从GNN和先验知识中受益。
图2:我们建议的学生模型的架构图。以中心节点 为例,学生模型从节点 的原始特征和统一的标签分布作为软标签开始,然后在每一层,将 的软标签预测更新为来自 的邻居的参数化标签传播(PLP)和 的特征变换(FT)的可训练组合。最终,将使学生与经过训练的教师的软标签预测之间的距离最小化。
在本小节中,我们将首先简要回顾传统的标签传播算法。然后,我们将介绍我们的PLP和FT模块及其可训练的组合。
2.3.1 标签传播
标签传播(LP)[40]是基于图的经典半监督学习模型。该模型仅遵循以下假设:由边连接(或占据相同流形)的节点极有可能共享相同的标签。基于此假设,标签将从标记的节点传播到未标记的节点以进行预测。
正式地,我们使用 表示LP的最终预测,使用 表示k轮迭代后的LP预测。在这个工作中,如果 是标记节点,我们将对节点 的预测初始化为一个独热编码向量。否则,我们将为每个未标记的节点 设置均匀分布,这表明所有类的概率在开始时都是相同的。初始化可以形式化为:
其中, 是节点 在第 次迭代中的预测概率分布。在第k+1次迭代时,LP将按照如下方式更新无标记节点 的预测:
其中, 时节点 的邻居集合, 是控制节点更新平滑度的超参。
注意LP没有需要训练的参数,因此以端到端的方式不能拟合教师模型的输出。因此,我们通过引入更多参数来提升LP的表达能力。
2.3.2 参数化标签传播模块
现在,我们将通过在LP中进一步参数化边缘权重来介绍我们的参数化标签传播(PLP)模块。如等式3所示,LP模型在传播过程中平等对待节点的所有邻居。但是,我们假设不同邻居对一个节点的重要性应该不同,这决定了节点之间的传播强度。更具体地说,我们假设某些节点的标签预测比其他节点更"自信"。例如,一个节点的预测标签与其大多数邻居相似。这样的节点将更有可能将其标签传播给邻居,并使它们保持不变。
形式化来说,我们将给每个节点v设置一个置信度分数 。在传播过程中,所有节点 的邻居和 自身将把他们的标签传播给 。基于置信值越大,边缘权值越大的直觉,我们为 重写了等式3中的预测更新函数如下:
其中 是节点 和节点 的边权,通过下面的 函数计算:
与LP相似, 按照等式2初始化,在传播过程中,每个标记点 的 仍然保持独热真实编码向量。
注意,作为可选项,我们可以进一步参数化置信度分数 用于归纳设置:
其中, 是一个可学习参数,将节点 的特征映射为置信度分数。
2.3.3 特征转换模块
注意,通过边缘传播标签的PLP模块强调了基于结构的先验知识。因此,我们还引入了特征变换(FT)模块作为补充预测机制。FT模块仅通过查看节点的原始特征来预测标签。形式化来说,用 表示FT模块的预测,我们使用两层MLP后接一个softmax函数来将特征转换为软标签预测:
注:虽然单层逻辑回归更具可解释性,但我们发现两层逻辑回归对于提高学生的模型能力是必要的。
2.3.4 可训练组合
现在我们将结合PLP和FT模块作为我们的完整学生模型。细节上,我们将为每个节点 学习一个可训练参数 ,来平衡PLP和FT之间的预测。换句话说,FT和PLP的预测将在每个传播步骤合并。我们将合并后的完整模型命名为CPF,等式4中的每个无标记节点 的预测更新公式可以重新写做:
其中边权 和初始化 与PLP模块一致。根据是否按照等式6参数化置信度分数 ,模型有两个变体,分别是归纳模型CPF-ind和转导模型CPF-tra。
2.4 整体算法与细节
假设我们的学生模型一共有K层,等式1中的蒸馏目标可以进一步写为:
其中, 是 范数,参数集合 包括PLP和FT之间的平衡参数 ,PLP模块内部的置信度参数 (或归纳设置下的参数 ),以及FT模块中MLP的参数 。还有一个重要的超参数:传播层数 。
2.5 对模型可解释性与计算复杂性的讨论
在本小节中,我们将讨论学习的学生模型的可解释性和算法的复杂性。
经过知识蒸馏后,我们的学生模型CPF会将特定节点的标签作为标签传播和基于特征的MLP的预测之间的加权平均值进行预测。平衡参数指示基于结构的LP还是基于特征的MLP对于节点 的预测更重要。LP机制几乎是透明的,我们可以轻松地找出节点 在每个迭代中受哪个邻居影响的程度。另一方面,对基于特征的MLP的理解可以通过现有工作[21]或直接查看不同特征的梯度来获得。因此,学习过的学生模型比GNN教师具有更好的解释性。
算法每次迭代(算法1的第3行到第13行)的时间复杂度和空间复杂度都是 ,这和数据集的规模线性相关。事实上,操作可以简单写成矩阵形式,对于真实数据集的训练过程,使用单GPU可以在几秒内完成。因此,我们提出的知识蒸馏框架的时间、空间效率都很高。
3 实验
在本节中,我们将从介绍实验中使用的数据集和教师模型开始。然后,我们将详细介绍教师模型和学生变体的实验设置。之后,我们将给出评估半监督节点分类的定量结果。我们还在不同数量的传播层和训练比率下进行实验,以说明算法的鲁棒性。最后,我们将提供定性案例研究和可视化效果,以更好地理解我们的学生模型CPF中的学习参数。
3.1 数据集
表1:数据集统计信息
我们使用五个公共基准数据集进行实验,数据集的统计数据如表1所示。如以前的文献[14,24,27]所做的那样,我们仅考虑最大的连通分量,并将边视为无向边。
根据先前工作[24]中的实验设置,我们从每个类别中随机抽取20个节点作为标记节点,30个用于验证节点,所有其他节点用于测试。
3.2 教师模型及其设置
为了进行全面比较,我们在我们的知识蒸馏框架中考虑了七个GNN模型作为教师模型;对于每个数据集和教师模型,我们测试下列学生变体:
PLP: 只考虑参数化标签传播机制的学生变体;
FT:只考虑特征转换机制的学生变体;
CPF-ind:归纳设置下的完整模型;
CPF-tra:转导设置下的完整模型。
3.3 分类结果分析
表2:GCN[12]和GAT[30]作为教师模型的分类准确率
表3:APPNP[13]和SGAE[8]作为教师模型的分类准确率
表4:SGC[33]和GCNII[4]作为教师模型的分类准确率
表5:GLP[15]作为教师模型的分类准确率
五个数据集、七个GNN教师模型、四个学生变体模型上的实验结果在表格2,3,4,5中展示。
3.4 不同传播层数的分析
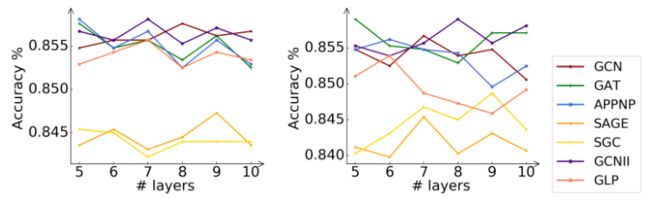
在本小节中,我们将研究关键超参数对学生模型CPF的体系结构(即传播层数)的影响。实际上,流行的GNN模型(例如GCN和GAT)对层数非常敏感。较大数量的层将导致过平滑的问题,并严重损害模型性能。因此,我们在Cora数据集上进行了实验,以进一步分析该超参数。
图3:Cora数据集上具有不同数量传播层的CPF-ind和CPF-tra的分类精度。图例表示指导学生的老师模式。
3.5 不同训练比例的分析
为了进一步证明该框架的有效性,我们在不同的训练比例下进行了额外的实验。具体来说,我们以Cora数据集为例,将每个类的标记节点数量从5个变化到50个。实验结果如图4所示。
图4:Cora数据集上不同数量的标记节点下的分类精度。子标题指示相应的教师模型。
3.6 可解释性分析
现在,我们将分析学习的学生模型CPF的可解释性。具体来说,我们将探究PLP和FT之间的学习平衡参数 以及每个节点的置信度得分 。我们的目标是找出哪种节点具有最大或最小的 和 。在本小节中,我们将使用由GCN和GAT教师模型指导的CPF-ind学生模型在Cora数据集上进行展示。
图5:用于可解释性分析的平衡参数 案例研究。此处的子标题表示该节点是按GCN/GAT作为教师模型,按大或小值选择的。
图6:用于可解释性分析的置信度得分 案例研究。此处的子标题表示该节点是按GCN/GAT作为教师模型,按大或小值选择的。
4 结论
在本文中,我们提出了一种有效的知识蒸馏框架,可以提取任意预训练的GNN(教师模型)的知识并将其注入精心设计的学生模型中。学生模型CPF被建立为两个简单预测机制的可训练组合:标签传播和特征转换,二者分别强调基于结构的先验知识和基于特征的先验知识。蒸馏后,学习的学生可以利用先验知识和GNN知识,从而超越GNN老师。在五个基准数据集上的实验结果表明,我们的框架可以通过更可解释的预测过程来一致,显着地改善所有七个GNN教师模型的分类精度。在不同数量的训练比率和传播层数上进行的附加实验证明了我们算法的鲁棒性。我们还提供了案例研究,以了解学生架构中学习到的平衡参数和置信度得分。
在未来的工作中,除了半监督节点分类之外,我们还将探索将我们的框架用于其他基于图的应用。例如,无监督节点聚类任务会很有趣,因为标签传播模式在没有标签的情况下不能应用。另一个方向是改进我们的框架,鼓励教师和学生模型互相学习,以取得更好的成绩。
说个正事哈
由于微信平台算法改版,公号内容将不再以时间排序展示,如果大家想第一时间看到我们的推送,强烈建议星标我们和给我们多点点【在看】。星标具体步骤为:
(1)点击页面最上方“深度学习自然语言处理”,进入公众号主页。
(2)点击右上角的小点点,在弹出页面点击“设为星标”,就可以啦。
投稿或交流学习,备注:昵称-学校(公司)-方向,进入DL&NLP交流群。
方向有很多:机器学习、深度学习,python,情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。
记得备注呦
整理不易,还望给个在看!
参考文献
[1] Charu C Aggarwal and ChengXiang Zhai. 2012. A survey of text classification algorithms. In Mining text data. Springer, 163--222.
[2] Kristen M Altenburger and Johan Ugander. 2017. Bias and variance in the social structure of gender. arXiv preprint arXiv:1705.04774 (2017).
[3] Smriti Bhagat, Graham Cormode, and S Muthukrishnan. 2011. Node classification in social networks. In Social network data analytics. Springer, 115--148.
[4] Ming Chen, Zhewei Wei, Zengfeng Huang, Bolin Ding, and Yaliang Li. 2020. Simple and deep graph convolutional networks. arXiv preprint arXiv:2007.02133 (2020).
[5] Finale Doshi-Velez and Been Kim. 2017. Towards a rigorous science of interpretable machine learning. arXiv preprint arXiv:1702.08608 (2017).
[6] Tommaso Furlanello, Zachary Lipton, Michael Tschannen, Laurent Itti, and Anima Anandkumar. 2018. Born Again Neural Networks. In International Conference on Machine Learning. 1607--1616.
[7] Justin Gilmer, Samuel S Schoenholz, Patrick F Riley, Oriol Vinyals, and George E Dahl. 2017. Neural message passing for Quantum chemistry. In Proceedings of the 34th International Conference on Machine Learning-Volume 70. 1263--1272.
[8] Will Hamilton, Zhitao Ying, and Jure Leskovec. 2017. Inductive representation learning on large graphs. In Advances in neural information processing systems. 1024--1034.
[9] Geoffrey Hinton, Oriol Vinyals, and Jeff Dean. 2015. Distilling the knowledge in a neural network. arXiv preprint arXiv:1503.02531 (2015).
[10] Thorsten Joachims. 2003. Transductive learning via spectral graph partitioning. In Proceedings of the Twentieth International Conference on International Conference on Machine Learning. 290--297.
[11] Diederik P Kingma and Jimmy Ba. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014).
[12] Thomas N Kipf and Max Welling. 2017. Semi-supervised classification with graph convolutional networks. In 5th International Conference on Learning Representations.
[13] Johannes Klicpera, Aleksandar Bojchevski, and Stephan Günnemann. 2018. Predict then Propagate: Graph Neural Networks meet Personalized PageRank. In International Conference on Learning Representations.
[14] Johannes Klicpera, Stefan Weißenberger, and Stephan Günnemann. 2019. Diffusion improves graph learning. In Advances in Neural Information Processing Systems. 13354--13366.
[15] Qimai Li, Xiao-Ming Wu, Han Liu, Xiaotong Zhang, and Zhichao Guan. 2019. Label efficient semi-supervised learning via graph filtering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 9582--9591.
[16] Rui Li, Chi Wang, and Kevin Chen-Chuan Chang. 2014. User profiling in an ego network: co-profiling attributes and relationships. In Proceedings of the 23^rd^ international conference on World wide web. 819--830.
[17] Miller McPherson, Lynn Smith-Lovin, and James M Cook. 2001. Birds of a feather: Homophily in social networks. Annual review of sociology 27, 1 (2001), 415--444.
[18] Galileo Namata, Ben London, Lise Getoor, Bert Huang, and UMD EDU. 2012. Query-driven active surveying for collective classification. In 10th International Workshop on Mining and Learning with Graphs, Vol. 8.
[19] Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, et al. 2019. Pytorch: An imperative style, high-performance deep learning library. In Advances in neural information processing systems. 8026--8037.
[20] Meng Qu, Yoshua Bengio, and Jian Tang. 2019. GMNN: Graph Markov Neural Networks. In International Conference on Machine Learning. 5241--5250.
[21] Marco Tulio Ribeiro, Sameer Singh, and Carlos Guestrin. 2016. "Why should I trust you?" Explaining the predictions of any classifier. In Proceedings of the 22^nd^ ACM SIGKDD international conference on knowledge discovery and data mining. 1135--1144.
[22] Franco Scarselli, Marco Gori, Ah Chung Tsoi, Markus Hagenbuchner, and Gabriele Monfardini. 2008. The graph neural network model. IEEE Transactions on Neural Networks 20, 1 (2008), 61--80.
[23] Prithviraj Sen, Galileo Namata, Mustafa Bilgic, Lise Getoor, Brian Galligher, and Tina Eliassi-Rad. 2008. Collective classification in network data. AI magazine 29, 3 (2008), 93--93.
[24] Oleksandr Shchur, Maximilian Mumme, Aleksandar Bojchevski, and Stephan Günnemann. 2018. Pitfalls of graph neural network evaluation. arXiv preprint arXiv:1811.05868 (2018).
[25] Yunsheng Shi, Zhengjie Huang, Shikun Feng, and Yu Sun. 2020. Masked Label Prediction: Unified Massage Passing Model for Semi-Supervised Classification. arXiv preprint arXiv:2009.03509 (2020).
[26] Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. 2014. Dropout: a simple way to prevent neural networks from overfitting. The journal of machine learning research 15, 1 (2014), 1929--1958.
[27] Ke Sun, Zhouchen Lin, and Zhanxing Zhu. 2020. Multi-Stage Self-Supervised Learning for Graph Convolutional Networks on Graphs with Few Labeled Nodes. In Thirty-Fourth AAAI Conference on Artificial Intelligence.
[28] Martin Szummer and Tommi Jaakkola. 2002. Partially labeled classification with Markov random walks. In Advances in neural information processing systems. 945--952.
[29] Lei Tang and Huan Liu. 2009. Scalable learning of collective behavior based on sparse social dimensions. In Proceedings of the 18th ACM conference on Information and knowledge management. 1107--1116.
[30] Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Liò, and Yoshua Bengio. 2018. Graph Attention Networks. In International Conference on Learning Representations.
[31] Hongwei Wang and Jure Leskovec. 2020. Unifying graph convolutional neural networks and label propagation. arXiv preprint arXiv:2002.06755 (2020).
[32] Minjie Wang, Lingfan Yu, Da Zheng, Quan Gan, Yu Gai, Zihao Ye, Mufei Li, Jinjing Zhou, Qi Huang, Chao Ma, et al. 2019. Deep graph library: Towards efficient and scalable deep learning on graphs. arXiv preprint arXiv:1909.01315 (2019).
[33] Felix Wu, Amauri Souza, Tianyi Zhang, Christopher Fifty, Tao Yu, and Kilian Weinberger. 2019. Simplifying Graph Convolutional Networks. In International Conference on Machine Learning. 6861--6871.
[34] Zonghan Wu, Shirui Pan, Fengwen Chen, Guodong Long, Chengqi Zhang, and S Yu Philip. 2020. A comprehensive survey on graph neural networks. IEEE Transactions on Neural Networks and Learning Systems (2020).
[35] Yiding Yang, Jiayan Qiu, Mingli Song, Dacheng Tao, and Xinchao Wang. 2020. Distilling Knowledge From Graph Convolutional Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 7074--7083.
[36] Zhitao Ying, Dylan Bourgeois, Jiaxuan You, Marinka Zitnik, and Jure Leskovec. 2019. Gnnexplainer: Generating explanations for graph neural networks. In Advances in Neural Information Processing Systems. 9240--9251.
[37] Wentao Zhang, Xupeng Miao, Yingxia Shao, Jiawei Jiang, Lei Chen, Olivier Ruas, and Bin Cui. 2020. Reliable Data Distillation on Graph Convolutional Network. In Proceedings of the 2020 ACM SIGMOD International Conference on Management of Data. 1399--1414.
[38] Dengyong Zhou, Olivier Bousquet, Thomas N Lal, Jason Weston, and Bernhard Schölkopf. 2004. Learning with local and global consistency. In Advances in neural information processing systems. 321--328.
[39] Jie Zhou, Ganqu Cui, Zhengyan Zhang, Cheng Yang, Zhiyuan Liu, Lifeng Wang, Changcheng Li, and Maosong Sun. 2018. Graph neural networks: A review of methods and applications. arXiv preprint arXiv:1812.08434 (2018).
[40] Xiaojin Zhu and Zoubin Ghahramani. 2002. Learning from labeled and unlabeled data with label propagation. Technical Report CMU-CALD-02-107, Carnegie Mellon University (2002).
[41] Xiaojin Zhu, Zoubin Ghahramani, and John Lafferty. 2003. Semi-supervised learning using Gaussian fields and harmonic functions. In Proceedings of the Twentieth International Conference on International Conference on Machine Learning. 912--919.