copulas对涉及时间连续随机过程的时变可靠性的影响研究（Matlab代码实现）

欢迎来到本博客❤️❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

目录

1 概述

2 运行结果

3 参考文献

4 Matlab代码实现

1 概述

   对于多功能机械系统而言，分析其可靠性的核心在于建立多功能表征量的联台分布函数(CDF);但是复杂的相关关系，使得常规构造CDF的方法存在难度。而Copula函数则可以很好地描述相关性，并建立多变量的联合分布函数。

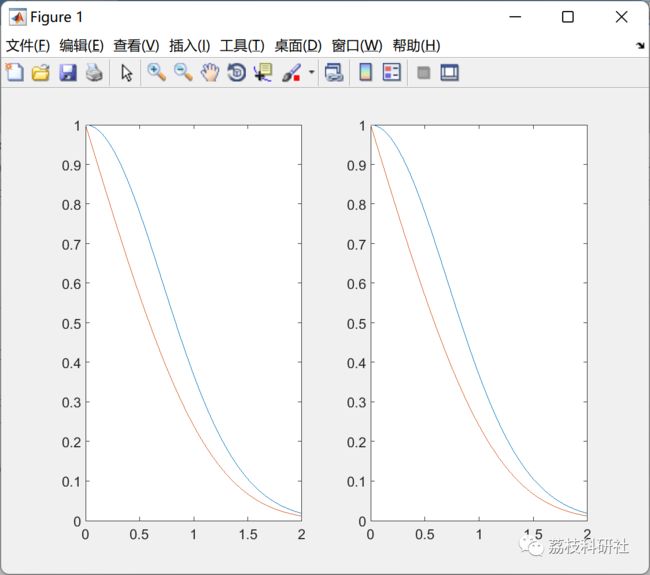
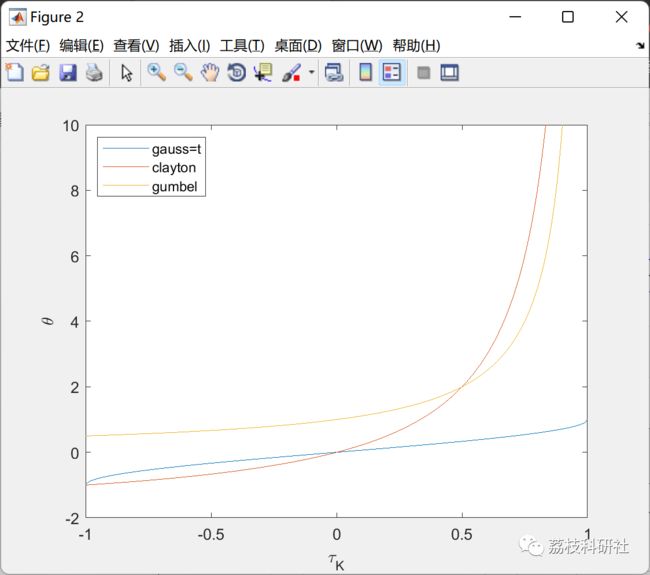
2 运行结果

部分代码：

clearvars
close all
clc

R   = mp('3');
rho = mp('0.999');
% integral2(@(x,y) mvnpdf([x, y], [0,0], [1, 0.5; 0.5, 1]), -Inf,R, R,Inf)
integral2(@(x,y) reshape(binormpdf([x(:), y(:)], [0,0], double([1, rho; rho, 1])), size(x)), -Inf,double(R), double(R),Inf, 'Abstol', 1e-16, 'Reltol', 1e-16)

p_s = normcdf(double(R));

% prone to catastrophic cancelation!!
p_s - copulacdf('Gaussian', [p_s, p_s], double(rho))

u = repmat(1-bivnor_mp(R,mp('-Inf'),0,50),1,2);

p_s - binorm_copulacdf_mp(u, rho)
 

clear all
close all
clc

% OPTIONS
%simulation number
N = 3;

L_meshed    = 1:1:1*365;
corr_length = 100;
pow         = 2;

%mean value
mu = 3500;

%standard deviation
sigma = 0.20*mu;

% CALCULATION
n_elem      = length(L_meshed)-1;
L_midpoint  = L_meshed(1:end-1) + diff(L_meshed)/2;

cov_matrix = element_cov_matrix(L_meshed, corr_length, pow);
%Cholesky decomposition of cov_matrix
% A = chol(cov_matrix,'lower');
% 
% ir1 = normrnd(mu, sigma, n_elem, N);
% dr1 = A*ir1;

r = mvnrnd(ones(n_elem,1)*mu, cov_matrix*sigma^2, N);

rr = zeros(size(r,1), length(L_meshed)*10);
calc_point = linspace(L_midpoint(1), L_midpoint(end), length(L_meshed)*10);
for i=1:size(r,1)
    rr(i,:) = interp1(L_midpoint, r(i,:), calc_point ,'spline');
end
%rr= r;
f_diag = figure('Position',[200, 200, 1200, 500]);
%f1 = plot(rr','black','LineWidth',2)   %black
f1 = plot(calc_point, rr','-','LineWidth',1);       %colored
grid on
hold on
% plot(calc_point, mean(rr),'blue','LineWidth',3)
% plot(calc_point, mean(rr)+std(rr),'red','LineWidth',3)
% plot(calc_point, mean(rr)-std(rr),'red','LineWidth',3)
ylim([0.9*min(min(rr)), 1.1*max(max(rr))])
% legend(f1,'simulation',...)
%         'Location','EastOutside')

% q = 500:100:7000;
% F = q;
% for i = 1:length(q)
%     id = max(rr,[],2) > q(i);
%     F(i) = sum(id)/N;
% end
% %save('p1.mat','p')
% qf          = q(1:end-1)+diff(q)/2;
% 
% f           = diff(F);
% scale       = trapz(qf,f);
% f           = f/scale;
% mu          = trapz(qf,f.*qf);
% var         = trapz(qf,f.*(qf-mu).^2);
% cov         = sqrt(var)/mu;
% 
% figure
% plot(q ,F)
% hold on
% plot(q, 1-normcdf(q, mu, mu*cov), 'r')
% grid on
% legend('numeric', 'mom normal')
% 
% mu
% cov

3 参考文献

[1]刘敬一,庄新臣,张玉刚,庞欢.基于Copula函数的多功能机械系统竞争失效分析方法[J].西北工业大学学报,2022,40(04):909-917.

[2]何浩祥,程扬,黄磊,陈旺,陈彦江.基于多元Copula函数的连续梁桥整体地震易损性分析[J].北京工业大学学报,2022,48(10):1018-1027.

4 Matlab代码实现