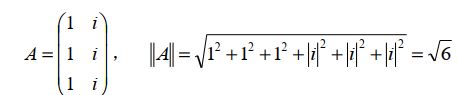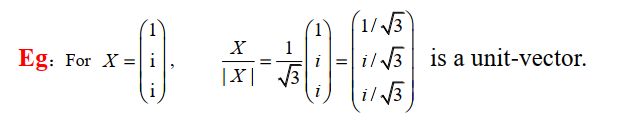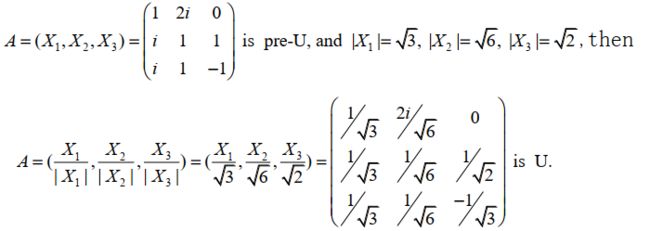【矩阵论】1.准备知识——复数域上的内积域正交阵
矩阵论
1. 准备知识——复数域上的矩阵与换位公式)
1. 准备知识——复数域上的内积域正交阵
1. 准备知识——相似对角化与合同&正定阵
2. 矩阵分解—— SVD准备知识——奇异值
2. 矩阵分解——SVD
2. 矩阵分解——QR分解
2. 矩阵分解——乔利斯分解&平方根公式
2. 矩阵分解——正规谱分解——正规阵
2. 矩阵分解——正规分解
2. 矩阵分解——单阵及特征值特征向量一些求法
1.7 内积
X = ( x 1 x 2 ⋮ x n ) , Y = ( y 1 y 2 ⋮ y n ) ∈ C n \begin{aligned} &X=\left( \begin{matrix} x_1\\x_2\\\vdots\\x_n \end{matrix} \right),Y=\left( \begin{matrix} y_1\\y_2\\\vdots\\y_n \end{matrix} \right)\in C^n \end{aligned} X=⎝ ⎛x1x2⋮xn⎠ ⎞,Y=⎝ ⎛y1y2⋮yn⎠ ⎞∈Cn
1.7.1 复向量内积
( X , Y ) = Δ Y H X = x 1 y 1 ‾ + x 2 y 2 ‾ + ⋯ + x n y n ‾ = ∑ i = 1 n x i y i ‾ = t r ( Y H X ) ( Y , X ) = X H Y = x 1 ‾ y 1 + x 2 ‾ y 2 + ⋯ + x n ‾ y 1 = ∑ i = 1 n x i ‾ y i = t r ( X H Y ) \begin{aligned} (X,Y)&\overset{\Delta}{=}Y^HX=x_1\overline{y_1}+x_2\overline{y_2}+\cdots+x_n\overline{y_n}=\sum\limits_{i=1}\limits^{n}x_i\overline{y_i}\\ &=tr(Y^HX)\\ (Y,X)&=X^HY=\overline{x_1}y_1+\overline{x_2}y_2+\cdots+\overline{x_n}y_1=\sum\limits_{i=1}\limits^{n}\overline{x_i}y_i\\ &=tr(X^HY) \end{aligned} (X,Y)(Y,X)=ΔYHX=x1y1+x2y2+⋯+xnyn=i=1∑nxiyi=tr(YHX)=XHY=x1y1+x2y2+⋯+xny1=i=1∑nxiyi=tr(XHY)
若取Y=X,则其内积
( X , X ) = X H X = x 1 x 1 ‾ + x 2 x 2 ‾ + ⋯ + x n x n ‾ = ∑ i = 1 n x i x i ‾ = ∣ x 1 ∣ 2 + ∣ x 2 ∣ 2 + ⋯ + ∣ x n ∣ 2 = ∣ X ∣ 2 = t r ( X H X ) = t r ( X X H ) \begin{aligned} (X,X)&=X^HX=x_1\overline{x_1}+x_2\overline{x_2}+\cdots+x_n\overline{x_n}=\sum\limits_{i=1}\limits^{n}x_i\overline{x_i}\\ &=\vert x_1 \vert^2+\vert x_2 \vert^2+\cdots+\vert x_n \vert^2 = \vert X \vert^2\\ &=tr(X^HX)=tr(XX^H) \end{aligned} (X,X)=XHX=x1x1+x2x2+⋯+xnxn=i=1∑nxixi=∣x1∣2+∣x2∣2+⋯+∣xn∣2=∣X∣2=tr(XHX)=tr(XXH)
向量内积性质
- ( X , X ) ≥ 0 (X,X)\ge 0 (X,X)≥0 ;若 X ≠ 0 , ( X , X ) ≥ 0 X\neq 0 ,(X,X)\ge 0 X=0,(X,X)≥0
- ( X , Y ) = ( Y , X ) ‾ (X,Y)=\overline{(Y,X)} (X,Y)=(Y,X)
- ( k X , Y ) = k ( X , Y ) , ( X , k Y ) = k ‾ ( X , Y ) (kX,Y)=k(X,Y),(X,kY)=\overline{k}(X,Y) (kX,Y)=k(X,Y),(X,kY)=k(X,Y)
- (X+Y,W)=(X,Y)+(X,W)
- ∣ ( X , Y ) ∣ 2 ≤ ∣ X ∣ ⋅ ∣ Y ∣ \vert (X,Y) \vert^2\le \vert X \vert\cdot\vert Y \vert ∣(X,Y)∣2≤∣X∣⋅∣Y∣
1.7.2 复矩阵内积
定义
( A , B ) = Δ t r ( A B H ) = t r ( A H B ) = ∑ a i j b i j ‾ , A , B ∈ C m , n ( A , A ) = t r ( A A H ) = t r ( A H A ) = ∑ a i j a i j ‾ = ∑ ∣ a i j ∣ 2 \begin{aligned} &(A,B)\overset{\Delta}{=}tr(AB^H)=tr(A^HB)=\sum a_{ij}\overline{b_{ij}},A,B\in C^{m,n}\\ &(A,A)=tr(AA^H)=tr(A^HA)=\sum a_{ij}\overline{a_{ij}}=\sum \vert a_{ij} \vert^2 \end{aligned} (A,B)=Δtr(ABH)=tr(AHB)=∑aijbij,A,B∈Cm,n(A,A)=tr(AAH)=tr(AHA)=∑aijaij=∑∣aij∣2
矩阵A的模长: ∣ ∣ A ∣ ∣ = ( A , A ) = t r ( A A H ) = ∑ ∣ a i j ∣ 2 \vert \vert A \vert \vert=\sqrt{(A,A)}=\sqrt{tr(AA^H)}=\sqrt{\sum\vert a_{ij} \vert^2} ∣∣A∣∣=(A,A)=tr(AAH)=∑∣aij∣2
性质
-
( A , A ) = t r ( A A H ) = ∑ ∣ a i j ∣ 2 ≥ 0 (A,A)=tr(AA^H)=\sum\vert a_{ij} \vert^2 \ge 0 (A,A)=tr(AAH)=∑∣aij∣2≥0 ;若 A ≠ 0 A\neq 0 A=0 ,则 ( A , A ) > 0 (A,A)>0 (A,A)>0
-
( A , B ) = ( B , A ) ‾ (A,B)=\overline{(B,A)} (A,B)=(B,A)
-
( k A , B ) = k ( A , B ) , ( A , k B ) = k ‾ ( A , B ) (kA,B)=k(A,B),(A,kB)=\overline{k}(A,B) (kA,B)=k(A,B),(A,kB)=k(A,B)
-
(A+B,D)=(A,D)+(B,D),(D,A+B)=(D,A)+(D,B)
-
∣ ( A , B ) ∣ 2 ≤ ∣ A ∣ ⋅ ∣ B ∣ \vert (A,B) \vert^2 \le \vert A\vert\cdot\vert B \vert ∣(A,B)∣2≤∣A∣⋅∣B∣
矩阵的内积形式
列分块
A = ( a 11 ⋯ a 1 p ⋮ ⋱ ⋮ a n 1 ⋯ a n p ) ∈ C n × p = ( α 1 , ⋯ , α p ) , 其中 α i 为 n 维列向量 ( n × 1 阶矩阵 ) A H = ( a 11 ‾ ⋯ a n 1 ‾ ⋮ ⋱ ⋮ a 1 p ‾ ⋯ a n p ‾ ) ∈ C p × n = ( α 1 ‾ T ⋮ α p ‾ T ) ,其中 α 1 ‾ T 是 n 维行向量 ( 1 × n 阶矩阵 ) \begin{aligned} A&=\left( \begin{matrix} &a_{11}\quad&\cdots&a_{1p}\\ &\vdots\quad&\ddots&\vdots\\ &a_{n1}\quad&\cdots&a_{np} \end{matrix} \right)\in C^{n\times p}\\ &=(\alpha_1,\cdots,\alpha_p),其中\alpha_i为n维列向量(n\times 1阶矩阵)\\\\ A^H&=\left( \begin{matrix} &\overline{a_{11}}\quad&\cdots\quad &\overline{a_{n1}}\\ &\vdots\quad &\ddots&\vdots\\ &\overline{a_{1p}}\quad&\cdots\quad &\overline{a_{np}}\\ \end{matrix} \right)\in C^{p\times n}\\ &=\left( \begin{matrix} \overline{\alpha_1}^T\\ \vdots\\ \overline{\alpha_p}^T \end{matrix} \right),其中\overline{\alpha_1}^T是n维行向量(1\times n阶矩阵)\\\\ \end{aligned} AAH=⎝ ⎛a11⋮an1⋯⋱⋯a1p⋮anp⎠ ⎞∈Cn×p=(α1,⋯,αp),其中αi为n维列向量(n×1阶矩阵)=⎝ ⎛a11⋮a1p⋯⋱⋯an1⋮anp⎠ ⎞∈Cp×n=⎝ ⎛α1T⋮αpT⎠ ⎞,其中α1T是n维行向量(1×n阶矩阵)
A H A = ( α 1 ‾ T ⋮ α p ‾ T ) ( α 1 , ⋯ , α p ) = ( α 1 ‾ T α 1 α 1 ‾ T α 2 ⋯ α 1 ‾ T α p α 2 ‾ T α 1 α 2 ‾ T α 2 ⋯ α 2 ‾ T α p ⋮ ⋮ ⋱ ⋮ α p ‾ T α 1 α p ‾ T α 2 ⋯ α p ‾ T α p ) = ( ( α 1 , α 1 ) ( α 2 , α 1 ) ⋯ ( α p , α 1 ) ( α 1 , α 2 ) ( α 2 , α 2 ) ⋯ ( α p , α 2 ) ⋮ ⋮ ⋱ ⋮ ( α 1 , α p ) ( α 2 , α p ) ⋯ ( α p , α p ) ) = ( ( α 1 , α 1 ) ‾ ( α 1 , α 2 ) ‾ ⋯ ( α 1 , α p ) ‾ ( α 2 , α 1 ) ‾ ( α 2 , α 2 ) ‾ ⋯ ( α 2 , α p ) ‾ ⋮ ⋮ ⋱ ⋮ ( α p , α 1 ) ‾ ( α p , α 2 ) ‾ ⋯ ( α p , α p ) ‾ ) \begin{aligned} A^HA&=\left( \begin{matrix} \overline{\alpha_1}^T\\ \vdots\\ \overline{\alpha_p}^T \end{matrix} \right)(\alpha_1,\cdots,\alpha_p)\\\\ &=\left( \begin{matrix} &\overline{\alpha_1}^T\alpha_1\quad&\overline{\alpha_1}^T\alpha_2\quad &\cdots&\overline{\alpha_1}^T\alpha_p\\ &\overline{\alpha_2}^T\alpha_1\quad&\overline{\alpha_2}^T\alpha_2\quad &\cdots&\overline{\alpha_2}^T\alpha_p\\ &\vdots\quad&\vdots\quad &\ddots\quad &\vdots\\ &\overline{\alpha_p}^T\alpha_1\quad&\overline{\alpha_p}^T\alpha_2\quad &\cdots&\overline{\alpha_p}^T\alpha_p \end{matrix} \right)\\\\ &=\left( \begin{matrix} &(\alpha_1,\alpha_1)\quad &(\alpha_2,\alpha_1)\quad&\cdots\quad &(\alpha_p,\alpha_1)\\ &(\alpha_1,\alpha_2)\quad &(\alpha_2,\alpha_2)\quad&\cdots\quad &(\alpha_p,\alpha_2)\\ &\vdots\quad&\vdots\quad &\ddots\quad &\vdots\\ &(\alpha_1,\alpha_p)\quad &(\alpha_2,\alpha_p)\quad&\cdots\quad &(\alpha_p,\alpha_p) \end{matrix} \right)\\\\ &=\left( \begin{matrix} &\overline{(\alpha_1,\alpha_1)}\quad &\overline{(\alpha_1,\alpha_2)}\quad&\cdots\quad &\overline{(\alpha_1,\alpha_p)}\\ &\overline{(\alpha_2,\alpha_1)}\quad &\overline{(\alpha_2,\alpha_2)}\quad&\cdots\quad &\overline{(\alpha_2,\alpha_p)}\\ &\vdots\quad&\vdots\quad &\ddots\quad &\vdots\\ &\overline{(\alpha_p,\alpha_1)}\quad &\overline{(\alpha_p,\alpha_2)}\quad&\cdots\quad &\overline{(\alpha_p,\alpha_p)} \end{matrix} \right)\\ \end{aligned} AHA=⎝ ⎛α1T⋮αpT⎠ ⎞(α1,⋯,αp)=⎝ ⎛α1Tα1α2Tα1⋮αpTα1α1Tα2α2Tα2⋮αpTα2⋯⋯⋱⋯α1Tαpα2Tαp⋮αpTαp⎠ ⎞=⎝ ⎛(α1,α1)(α1,α2)⋮(α1,αp)(α2,α1)(α2,α2)⋮(α2,αp)⋯⋯⋱⋯(αp,α1)(αp,α2)⋮(αp,αp)⎠ ⎞=⎝ ⎛(α1,α1)(α2,α1)⋮(αp,α1)(α1,α2)(α2,α2)⋮(αp,α2)⋯⋯⋱⋯(α1,αp)(α2,αp)⋮(αp,αp)⎠ ⎞
行分块
A = ( a 11 ⋯ a 1 p ⋮ ⋱ ⋮ a n 1 ⋯ a n p ) ∈ C n × p = ( α 1 α 2 ⋮ α n ) , 其中 α i 为 p 维行向量 ( 1 × p 阶矩阵 ) A H = ( α 1 ‾ T α 2 ‾ T ⋯ α n ‾ T ) , 其中 α i ‾ T 为 p 维列向量 ( p × 1 阶矩阵 ) \begin{aligned} A&=\left( \begin{matrix} &a_{11}\quad&\cdots&a_{1p}\\ &\vdots\quad&\ddots&\vdots\\ &a_{n1}\quad&\cdots&a_{np} \end{matrix} \right)\in C^{n\times p}\\ &=\left( \begin{matrix} \alpha_1\\ \alpha_2\\ \vdots\\ \alpha_n \end{matrix} \right),其中\alpha_i为p维行向量(1\times p阶矩阵)\\\\ A^H&=\left( \begin{matrix} \overline{\alpha_1}^T\quad \overline{\alpha_2}^T\quad \cdots\quad \overline{\alpha_n}^T \end{matrix} \right),其中\overline{\alpha_i}^T 为p维列向量(p\times 1阶矩阵) \end{aligned} AAH=⎝ ⎛a11⋮an1⋯⋱⋯a1p⋮anp⎠ ⎞∈Cn×p=⎝ ⎛α1α2⋮αn⎠ ⎞,其中αi为p维行向量(1×p阶矩阵)=(α1Tα2T⋯αnT),其中αiT为p维列向量(p×1阶矩阵)
A A H = ( α 1 α 2 ⋮ α n ) ( α 1 ‾ T α 2 ‾ T ⋯ α n ‾ T ) = ( α 1 α 1 ‾ T α 1 α 2 ‾ T ⋯ α 1 α n ‾ T α 2 α 1 ‾ T α 2 α 2 ‾ T ⋯ α 2 α n ‾ T ⋮ ⋮ ⋱ ⋮ α n α 1 ‾ T α n α 2 ‾ T ⋯ α n α n ‾ T ) = ( ( α 1 , α 1 ) ( α 1 , α 2 ) ⋯ ( α 1 , α n ) ( α 2 , α 1 ) ( α 2 , α 2 ) ⋯ ( α 2 , α n ) ⋮ ⋮ ⋱ ⋮ ( α n , α 1 ) ( α n , α 2 ) ⋯ ( α n , α n ) ) \begin{aligned} AA^H&=\left( \begin{matrix} \alpha_1\\ \alpha_2\\ \vdots\\ \alpha_n \end{matrix} \right)\left( \begin{matrix} \overline{\alpha_1}^T\quad \overline{\alpha_2}^T\quad \cdots\quad \overline{\alpha_n}^T \end{matrix} \right)\\\\ &=\left( \begin{matrix} &\alpha_1\overline{\alpha_1}^T\quad &\alpha_1\overline{\alpha_2}^T\quad&\cdots\quad &\alpha_1\overline{\alpha_n}^T\\ &\alpha_2\overline{\alpha_1}^T\quad &\alpha_2\overline{\alpha_2}^T\quad&\cdots\quad &\alpha_2\overline{\alpha_n}^T\\ &\vdots\quad &\vdots\quad &\ddots\quad &\vdots\\ &\alpha_n\overline{\alpha_1}^T &\quad\alpha_n\overline{\alpha_2}^T\quad&\cdots\quad &\alpha_n\overline{\alpha_n}^T \end{matrix} \right)\\\\ &=\left( \begin{matrix} &(\alpha_1,\alpha_1)\quad &(\alpha_1,\alpha_2)\quad &\cdots\quad &(\alpha_1,\alpha_n)\\ &(\alpha_2,\alpha_1)\quad &(\alpha_2,\alpha_2)\quad &\cdots\quad &(\alpha_2,\alpha_n)\\ &\vdots\quad &\vdots\quad &\ddots\quad &\vdots\\ &(\alpha_n,\alpha_1)\quad &(\alpha_n,\alpha_2)\quad &\cdots\quad &(\alpha_n,\alpha_n) \end{matrix} \right) \end{aligned} AAH=⎝ ⎛α1α2⋮αn⎠ ⎞(α1Tα2T⋯αnT)=⎝ ⎛α1α1Tα2α1T⋮αnα1Tα1α2Tα2α2T⋮αnα2T⋯⋯⋱⋯α1αnTα2αnT⋮αnαnT⎠ ⎞=⎝ ⎛(α1,α1)(α2,α1)⋮(αn,α1)(α1,α2)(α2,α2)⋮(αn,α2)⋯⋯⋱⋯(α1,αn)(α2,αn)⋮(αn,αn)⎠ ⎞
1.8 正交
1.8.1 向量正交
X = ( x 1 x 2 ⋮ x n ) , Y = ( y 1 y 2 ⋮ y n ) ∈ C n \begin{aligned} X&=\left( \begin{matrix} x_1\\ x_2\\ \vdots\\ x_n \end{matrix} \right),Y=\left( \begin{matrix} y_1\\ y_2\\ \vdots\\ y_n \end{matrix} \right)\in C^{n} \end{aligned} X=⎝ ⎛x1x2⋮xn⎠ ⎞,Y=⎝ ⎛y1y2⋮yn⎠ ⎞∈Cn
X ⊥ Y ⟺ ( X , Y ) = 0 = x 1 y 1 ‾ + x 2 y 2 ‾ + ⋯ + x n y n ‾ = x 1 ‾ y 1 + x 2 ‾ y 2 + ⋯ + x n ‾ y n ‾ = ( Y , X ) \begin{aligned} X\bot Y\iff (X,Y)=0&=x_1\overline{y_1}+x_2\overline{y_2}+\cdots+x_n\overline{y_n}\\ &=\overline{\overline{x_1}y_1+\overline{x_2}y_2+\cdots+\overline{x_n}y_n}\\=(Y,X) \end{aligned} X⊥Y⟺(X,Y)=0=(Y,X)=x1y1+x2y2+⋯+xnyn=x1y1+x2y2+⋯+xnyn
正交性质
-
X ⊥ Y ⇒ a X ⊥ b Y X\bot Y\Rightarrow aX\bot bY X⊥Y⇒aX⊥bY
证: ( a X , b Y ) = b ‾ Y H a X = a b ‾ Y H X = a b ‾ ( X , Y ) = 0 (aX,bY)=\overline{b}Y^HaX=a\overline{b}Y^HX=a\overline{b}(X,Y)=0 (aX,bY)=bYHaX=abYHX=ab(X,Y)=0
-
勾股定理: X 1 ⊥ X 2 ⊥ ⋯ ± X n ⇒ ∣ c 1 X 1 ± c 2 X 2 ± ⋯ ± c n X n ∣ 2 = ∣ c 1 X 1 ∣ 2 + ∣ c 2 X 2 ∣ 2 + ⋯ + ∣ c n X n ∣ 2 X_1\bot X_2\bot \cdots \pm X_n\Rightarrow \vert c_1X_1\pm c_2X_2\pm \cdots \pm c_nX_n\vert^2=\vert c_1X_1\vert^2+\vert c_2X_2\vert^2+\cdots+\vert c_nX_n\vert^2 X1⊥X2⊥⋯±Xn⇒∣c1X1±c2X2±⋯±cnXn∣2=∣c1X1∣2+∣c2X2∣2+⋯+∣cnXn∣2
此时, X 1 , X 2 , ⋯ , x n X_1,X_2,\cdots,x_n X1,X2,⋯,xn 称为一个正交组
1.8.2 单位向量
若 X ≠ 0 ⃗ X\neq \vec{0} X=0 , X ∣ X ∣ \frac{X}{\vert X \vert} ∣X∣X 是一个单位向量( ∣ X ∣ X ∣ ∣ = 1 \vert \frac{X}{\vert X \vert} \vert=1 ∣∣X∣X∣=1)
1.8.3 U阵(正交阵)
预:非单位列向量
半:p个n维列向量(p α 1 , α 2 , ⋯ , α p 是 n 维列向量,且 p ≤ n ,且 α 1 ⊥ α 2 ⊥ ⋯ ⊥ α p 则称 A = ( α 1 , α 2 , ⋯ , α p ) 为预半 U 阵 \alpha_1,\alpha_2,\cdots,\alpha_p 是n维列向量,且p\le n,且\alpha_1\bot\alpha_2\bot \cdots\bot\alpha_p\\ 则称A=(\alpha_1,\alpha_2,\cdots,\alpha_p) 为预半U阵 α1,α2,⋯,αp是n维列向量,且p≤n,且α1⊥α2⊥⋯⊥αp则称A=(α1,α2,⋯,αp)为预半U阵 A = ( α 1 , α 2 , ⋯ , α p ) 是预半 U 阵 ⟺ A H A = ( ( α 1 , α 1 ) ⋯ 0 ⋮ ⋱ 0 0 ⋯ ( α p , α p ) ) 是对角阵 其中, α 1 , α 2 , ⋯ , α p 是 n 维列向量 \begin{aligned} A&=(\alpha_1,\alpha_2,\cdots,\alpha_p) 是预半U阵\\ &\iff A^HA=\left( \begin{matrix} &(\alpha_1,\alpha_1)&\cdots&0\\ &\vdots&\ddots&0\\ &0&\cdots&(\alpha_p,\alpha_p) \end{matrix} \right)是对角阵\\ &其中,\alpha_1,\alpha_2,\cdots,\alpha_p是n维列向量 \end{aligned} A=(α1,α2,⋯,αp)是预半U阵⟺AHA=⎝ ⎛(α1,α1)⋮0⋯⋱⋯00(αp,αp)⎠ ⎞是对角阵其中,α1,α2,⋯,αp是n维列向量 证明: 区分 : A H A A^HA AHA 是 p × p p \times p p×p 阶满秩方阵,而 A A H AA^H AAH 是 n × n n\times n n×n 不满秩方阵 A = ( α 1 , α 2 , ⋯ , α p ) 是预半 U 阵,其中 α i 是 n 维列向量,若满足 ∣ α 1 ∣ = ∣ α 2 ∣ = ⋯ = ∣ α p ∣ = 1 , 则 A 为半 U 阵 \begin{aligned} &A=(\alpha_1,\alpha_2,\cdots,\alpha_p)是预半U阵,其中\alpha_i是n维列向量,若满足\\ &\vert \alpha_1 \vert=\vert \alpha_2 \vert=\cdots=\vert \alpha_p \vert = 1,则A为半U阵 \end{aligned} A=(α1,α2,⋯,αp)是预半U阵,其中αi是n维列向量,若满足∣α1∣=∣α2∣=⋯=∣αp∣=1,则A为半U阵 A = ( α 1 , ⋯ , α p ) 是半 U 阵 ⟺ α 1 ⊥ ⋯ ⊥ α p , 且 ∣ α 1 ∣ = ⋯ = ∣ α p ∣ = 1 ⟺ A H A = I p \begin{aligned} A=(\alpha_1,\cdots,\alpha_p)是半U阵&\iff \alpha_1\bot\cdots\bot\alpha_p,且\vert \alpha_1 \vert=\cdots=\vert \alpha_p \vert=1\\ &\iff A^HA=I_{p} \end{aligned} A=(α1,⋯,αp)是半U阵⟺α1⊥⋯⊥αp,且∣α1∣=⋯=∣αp∣=1⟺AHA=Ip 保模长 A为半U阵,则 ∣ A x ∣ 2 = ∣ x ∣ 2 \vert Ax \vert^2=\vert x \vert^2 ∣Ax∣2=∣x∣2 ∣ A x ∣ 2 = ( A x ) H ( A x ) = x H A H A x = ∣ X ∣ 2 \vert Ax \vert^2=(Ax)^H(Ax)=x^HA^HAx=\vert X\vert^2 ∣Ax∣2=(Ax)H(Ax)=xHAHAx=∣X∣2 保正交 A为半U阵, x ⊥ y x\bot y x⊥y ,则 A x ⊥ A y Ax\bot Ay Ax⊥Ay α 1 , α 2 , ⋯ , α n 是 n 维列向量,且 α 1 ⊥ α 2 ⊥ ⋯ ⊥ α n , 则 A = ( α 1 , α 2 , ⋯ , α n ) 是预 U 阵 \begin{aligned} &\alpha_1,\alpha_2,\cdots,\alpha_n是n维列向量,且\alpha_1\bot\alpha_2\bot\cdots\bot\alpha_n ,\\ &则A=(\alpha_1,\alpha_2,\cdots,\alpha_n)是预U阵 \end{aligned} α1,α2,⋯,αn是n维列向量,且α1⊥α2⊥⋯⊥αn,则A=(α1,α2,⋯,αn)是预U阵 eg A = ( α 1 , α 2 , ⋯ , α n ) ⟺ A H A = ( ( α 1 , α 1 ) ⋯ 0 ⋮ ⋱ 0 0 ⋯ ( α n , α n ) ) 是对角阵 其中, α 1 , α 2 , ⋯ , α p 是 n 维列向量 \begin{aligned} A&=(\alpha_1,\alpha_2,\cdots,\alpha_n)\\ &\iff A^HA=\left( \begin{matrix} &(\alpha_1,\alpha_1)&\cdots&0\\ &\vdots&\ddots&0\\ &0&\cdots&(\alpha_n,\alpha_n) \end{matrix} \right)是对角阵\\ &其中,\alpha_1,\alpha_2,\cdots,\alpha_p是n维列向量 \end{aligned} A=(α1,α2,⋯,αn)⟺AHA=⎝ ⎛(α1,α1)⋮0⋯⋱⋯00(αn,αn)⎠ ⎞是对角阵其中,α1,α2,⋯,αp是n维列向量 等价判定 A 是预 U 阵且 ∣ α 1 ∣ = ⋯ = ∣ α n ∣ = 1 , 则 A 是一个 U 阵 ( 正交阵 ) \begin{aligned} A是预U阵且 \vert \alpha_1 \vert=\cdots=\vert \alpha_n \vert=1,则A是一个U阵(正交阵) \end{aligned} A是预U阵且∣α1∣=⋯=∣αn∣=1,则A是一个U阵(正交阵) A = ( α 1 , ⋯ , α n ) ⟺ A H A = ( 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ 1 ) = I 是单位阵 \begin{aligned} A&=(\alpha_1,\cdots,\alpha_n)\\ &\iff A^HA=\left( \begin{matrix} &1&0&\cdots&0\\ &0&1&\cdots&0\\ &\vdots&\vdots&\ddots&\vdots\\ &0&0&\cdots&1 \end{matrix} \right)=I是单位阵 \end{aligned} A=(α1,⋯,αn)⟺AHA=⎝ ⎛10⋮001⋮0⋯⋯⋱⋯00⋮1⎠ ⎞=I是单位阵 1. A 是 U 阵 ⟺ A H A = I ⟺ A − 1 A = I ⟺ A A H = I ⟺ A = ( α 1 , α 2 , ⋯ , α n ) ,且 α 1 ⊥ α 2 , ⋯ ⊥ α n , 且 ∣ α 1 ∣ = ⋯ = ∣ α n ∣ = 1 2. ∣ A x ∣ 2 = ∣ x ∣ 2 , A 是 U 阵 ∵ ∣ A x ∣ 2 = ( A x ) H ( A x ) = x H A H A x = x H I x = ( x , x ) = ∣ x ∣ 2 3. x ⊥ y ⇒ A x ⊥ A y , A 是 U 阵 ∵ ( A x , A y ) = ( A y ) H A x = y H A H A x = ( x , y ) = 0 ⟺ A x ⊥ A y 4. ( A x , A y ) = ( x , y ) , A 是 U 阵 \begin{aligned} &1. A是U阵\iff A^HA=I\iff A^{-1}A=I\iff AA^H=I\\ &\iff A=(\alpha_1,\alpha_2,\cdots,\alpha_n) ,且\alpha_1\bot\alpha_2,\cdots\bot\alpha_n,且\vert \alpha_1\vert=\cdots=\vert\alpha_n\vert=1\\\\ &2.\vert Ax\vert^2=\vert x \vert^2,A是U阵\\ &\because \vert Ax\vert^2 = (Ax)^H(Ax)=x^HA^HAx=x^HIx=(x,x)=\vert x \vert^2\\\\ &3.x\bot y \Rightarrow Ax\bot Ay,A是U阵\\ &\because (Ax,Ay)=(Ay)^HAx=y^HA^HAx=(x,y)=0\iff Ax\bot Ay\\\\ &4.(Ax,Ay)=(x,y),A是U阵 \end{aligned} 1.A是U阵⟺AHA=I⟺A−1A=I⟺AAH=I⟺A=(α1,α2,⋯,αn),且α1⊥α2,⋯⊥αn,且∣α1∣=⋯=∣αn∣=12.∣Ax∣2=∣x∣2,A是U阵∵∣Ax∣2=(Ax)H(Ax)=xHAHAx=xHIx=(x,x)=∣x∣23.x⊥y⇒Ax⊥Ay,A是U阵∵(Ax,Ay)=(Ay)HAx=yHAHAx=(x,y)=0⟺Ax⊥Ay4.(Ax,Ay)=(x,y),A是U阵 A = ( α 1 , ⋯ , α n ) 是预 U 阵 ⇒ A = ( α 1 ∣ α 1 ∣ , α 2 ∣ α 2 ∣ , ⋯ , α n ∣ α n ∣ ) 是 U 阵 \begin{aligned} A=(\alpha_1,\cdots,\alpha_n) 是预U阵\Rightarrow A=(\frac{\alpha_1}{\vert \alpha_1\vert},\frac{\alpha_2}{\vert \alpha_2\vert},\cdots,\frac{\alpha_n}{\vert \alpha_n \vert})是U阵 \end{aligned} A=(α1,⋯,αn)是预U阵⇒A=(∣α1∣α1,∣α2∣α2,⋯,∣αn∣αn)是U阵 若 A = ( α 1 , α 2 , ⋯ , α n ) 为 U 阵,则 1. k = ± 1 , k A = ( k α 1 , k α 2 , ⋯ , k α n ) 为 U 阵 2. B = ( β 1 , β 2 , ⋯ , β n ) 为 U 阵,其中 β 组为 α 组的重排 3. ( 封闭性 ) 若 A 、 B 为同阶 U 阵,则 A B 也为 U 阵 \begin{aligned} 若A&=(\alpha_1,\alpha_2,\cdots,\alpha_n) 为U阵,则\\ &1.k=\pm1,kA=(k\alpha_1,k\alpha_2,\cdots,k\alpha_n)为U阵\\ &2.B=(\beta_1,\beta_2,\cdots,\beta_n) 为U阵,其中\beta组为\alpha组的重排\\ &3.(封闭性)若A、B为同阶U阵,则AB也为U阵 \end{aligned} 若A=(α1,α2,⋯,αn)为U阵,则1.k=±1,kA=(kα1,kα2,⋯,kαn)为U阵2.B=(β1,β2,⋯,βn)为U阵,其中β组为α组的重排3.(封闭性)若A、B为同阶U阵,则AB也为U阵 若 α = ( a 1 a 2 ⋮ a n ) ∈ C , A = I n − 2 α α H ∣ α ∣ 2 是一个 U 阵 1. A H = A 且 A 2 = I ( A − 1 = A ) 2. A 为 U 阵 ( A H A = I ) 证明 : 1. A 2 = ( I n − 2 α α H ∣ α ∣ 2 ) ( I n − 2 α α H ∣ α ∣ 2 ) = I n 2 − 4 α α H ∣ α ∣ 2 + 4 ( α α H ) ( α α H ) ∣ α ∣ 4 = I n − 4 α α H ∣ α ∣ 2 + 4 α ( α H α ) α H ∣ α ∣ 4 = I n − 4 α α H ∣ α ∣ 2 + 4 α ( ∣ α ∣ 2 ) α H ∣ α ∣ 4 = I n − 4 α α H ∣ α ∣ 2 + 4 α α H ∣ α ∣ 2 = I n 2. A H A = ( I n − 2 α α H ∣ α ∣ 2 ) H ( I n − 2 α α H ∣ α ∣ 2 ) = ( I n − 2 α α H ∣ α ∣ 2 ) ( I n − 2 α α H ∣ α ∣ 2 ) = A 2 = I ∴ A 是 U 阵 \begin{aligned} 若\alpha&=\left( \begin{matrix} a_1\\a_2\\\vdots \\ a_n \end{matrix} \right)\in C,A=I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2}是一个U阵\\\\ &1.A^H=A且A^2=I(A^{-1}=A)\\ &2.A为U阵(A^HA=I)\\\\ 证明: 1.A^2&=(I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2})(I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2})\\ &=I_n^2-\frac{4\alpha\alpha^H}{\vert \alpha \vert^2}+\frac{4(\alpha\alpha^H)(\alpha\alpha^H)}{\vert \alpha\vert^4}=I_n-\frac{4\alpha\alpha^H}{\vert \alpha \vert^2}+\frac{4\alpha(\alpha^H\alpha)\alpha^H}{\vert \alpha\vert^4} \\ &=I_n-\frac{4\alpha\alpha^H}{\vert \alpha \vert^2}+\frac{4\alpha(\vert \alpha\vert^2)\alpha^H}{\vert \alpha\vert^4}=I_n-\frac{4\alpha\alpha^H}{\vert \alpha \vert^2}+\frac{4\alpha\alpha^H}{\vert \alpha \vert^2}=I_n\\ 2.A^HA&=(I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2})^H(I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2})\\ &=(I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2})(I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2})=A^2=I\\ &\therefore A是U阵 \end{aligned} 若α证明:1.A22.AHA=⎝ ⎛a1a2⋮an⎠ ⎞∈C,A=In−∣α∣22ααH是一个U阵1.AH=A且A2=I(A−1=A)2.A为U阵(AHA=I)=(In−∣α∣22ααH)(In−∣α∣22ααH)=In2−∣α∣24ααH+∣α∣44(ααH)(ααH)=In−∣α∣24ααH+∣α∣44α(αHα)αH=In−∣α∣24ααH+∣α∣44α(∣α∣2)αH=In−∣α∣24ααH+∣α∣24ααH=In=(In−∣α∣22ααH)H(In−∣α∣22ααH)=(In−∣α∣22ααH)(In−∣α∣22ααH)=A2=I∴A是U阵 eg :预-半U阵(预-半正交阵)
判定
半U阵(半正交阵)
判定
性质
预-U阵(预-单位正交阵)
X 1 = ( 1 i i ) , X 2 = ( 2 i 1 1 ) , X 3 = ( 0 1 − 1 ) ( X 1 , X 2 ) = 0 , ( X 2 , X 3 ) = 0 , ( X 1 , X 3 ) = 0 , ∴ X 1 ⊥ X 2 ⊥ X 3 , A = ( X 1 , X 2 , X 3 ) 是预 − U 阵 \begin{aligned} &X_1=\left( \begin{matrix} 1\\i\\i \end{matrix} \right),X_2=\left( \begin{matrix} 2i\\1\\1 \end{matrix} \right),X_3=\left( \begin{matrix} 0\\1\\-1 \end{matrix} \right)\\\\ &(X_1,X_2)=0,(X_2,X_3)=0,(X_1,X_3)=0,\\\\ &\therefore X_1\bot X_2\bot X_3,A=(X_1,X_2,X_3)是预-U阵 \end{aligned} X1=⎝ ⎛1ii⎠ ⎞,X2=⎝ ⎛2i11⎠ ⎞,X3=⎝ ⎛01−1⎠ ⎞(X1,X2)=0,(X2,X3)=0,(X1,X3)=0,∴X1⊥X2⊥X3,A=(X1,X2,X3)是预−U阵判定
U阵(A正交阵)
判定
性质
预U阵与U阵
U阵构造新U阵
向量构造U阵
α = ( 1 1 1 ) , 其 U 阵为 I 3 − 2 α α H ∣ α ∣ 2 = ( 1 0 0 0 1 0 0 0 1 ) − 2 3 ( 1 1 1 1 1 1 1 1 1 ) = ( 1 3 − 2 3 − 2 3 − 2 3 1 3 − 2 3 − 2 3 − 2 3 1 3 ) \begin{aligned} \alpha=\left( \begin{matrix} 1\\1\\1 \end{matrix} \right),其U阵为 I_3-\frac{2\alpha\alpha^H}{\vert \alpha\vert^2}&=\left( \begin{matrix} &1&0&0\\&0&1&0\\&0&0&1\\ \end{matrix} \right)-\frac{2}{3}\left( \begin{matrix} &1&1&1\\&1&1&1\\&1&1&1\\ \end{matrix} \right)\\ &=\left( \begin{matrix} &\frac{1}{3}&-\frac{2}{3}&-\frac{2}{3}\\ &-\frac{2}{3}&\frac{1}{3}&-\frac{2}{3}\\ &-\frac{2}{3}&-\frac{2}{3}&\frac{1}{3}\\ \end{matrix} \right) \end{aligned} α=⎝ ⎛111⎠ ⎞,其U阵为I3−∣α∣22ααH=⎝ ⎛100010001⎠ ⎞−32⎝ ⎛111111111⎠ ⎞=⎝ ⎛31−32−32−3231−32−32−3231⎠ ⎞