机器学习2--朴素贝叶斯
文章目录
- 1 统计学基础
-
-
- 1.1 统计与概率的基本知识
-
- 1.1.1基本概念
- 1.1.2概率分布
-
- 离散分布
-
- 表所示
- 用图表示为
- 写成函数的形式
- 连续分布
-
- 表格表示
- 图形化表示为,
- 函数表达式:
- 最大熵原理
- 多变量(联合)分布,
-
- 离散的联合概率分布
- 连续的联合概率分布
- 1.2.3 独立和条件独立
-
- 条件概率
- 独立性
- 条件独立
- 1.2 统计与概率研究问题的区别
-
- 2 贝叶斯分类器
-
- 2.1贝叶斯公式
- 2.2贝叶斯决策论
- 2.3MLE&MAP&贝叶斯估计
-
- 抛硬币
- 程序实现--高斯分布
- 结论
- 2.4 朴素贝叶斯
-
- 2.4.1 垃圾邮件分类
- 2.5 半朴素贝叶斯
- 2.6 贝叶斯网
- 3. Questions and Answers
1 统计学基础
1.1 统计与概率的基本知识
1.1.1基本概念
- 采样空间 sample space Ω \Omega Ω: 随机试验的所有可能输出,掷一次硬币的所有结构,扔一次骰子的所有结果。
- 事件event: 事件A时采样空间 Ω \Omega Ω的一个子集。硬币正面,骰子点数不小4
- 事件概率:P(A)
- 概率公理
(i)非负性:对任意事件 A, P(A) ≥ 0
(ii) P(Ω) = 1
(iii) σ可加:对任意不相交事件Ai,事件并集的概率等于事件概率之和 - 随机变量X: 将事件映射到实数域,随机变量也是函数 X ; Ω → R X; \Omega \to R X;Ω→R
example:P(a < X < b) = P(w: a < X(w) < b)
- X(w) = 1,我们班( Ω \Omega Ω )上课第一个睡着的同学(w)是男生
- X(w)<60,在可能获得的成绩( Ω \Omega Ω)里,最后不及格的分数(w)
1.1.2概率分布
可参考之前的博客[https://blog.csdn.net/qq_36097393/article/details/88973855](Probability distribution 概率分布)
在概率论和统计学中,概率分布就是数学函数。概率分布提供了实验中不同输出的概率。分为离散分布和连续分布
离散分布
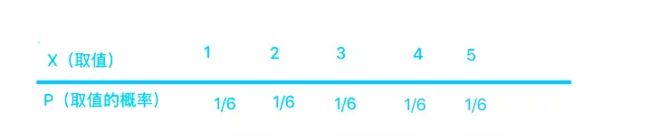
掷骰子的结果的概率及其分布
表所示
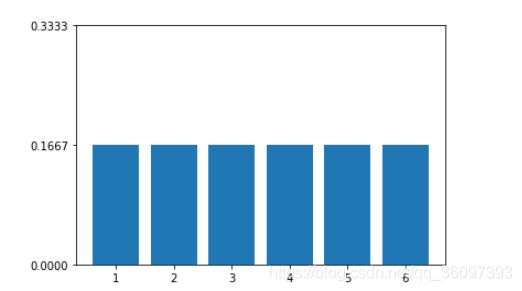
用图表示为
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.bar([1,2,3,4,5,6], [1/6,1/6,1/6,1/6,1/6,1/6,])
ax.set_ylim(0, 1/3)
ax.set_yticks(np.arange(0, 1/3+0.01, 1/6))
plt.show
写成函数的形式
p ( x ) = { 1 6 x = 1 1 6 x = 2 ⋯ x = . . . 1 6 x = 6 p(x ) = \left\{ \begin{aligned} &\frac{1}{6} \quad x = 1\\ &\frac{1}{6} \quad x = 2\\ &\cdots \quad x = ...\\ &\frac{1}{6} \quad x = 6\\ \end{aligned} \right. p(x)=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧61x=161x=2⋯x=...61x=6
伯努利分布:Ber§
二项分布:BIn(n,p)
连续分布
参考应该如何理解概率分布函数和概率密度函数?
离散型随机变量可以将概率全部列出来,可以写成分段函数,或者画直方图。连续分布如何表示
我们知道对于连续分布,一点的概率为0,因为对PDF的积分等于0,只有一个小区间有值.
对于正态分布x~N(0,1)
表格表示
| 区间 | [- ∞ , − 1 \infty,-1 ∞,−1] | [-2,0] | [0,2] | [+ ∞ , 0 \infty,0 ∞,0] |
|---|---|---|---|---|
| 概率 | 2.5% | 47.5% | 47.5% | 2.5% |
当然也可以等分区间。在每个区间h上的概率为P(x) =F(x+h) - F(x)] ,[F(x+h) - F(x)]/h就可以解释成x点附件h这么长的区间(x,x+h)内,单位长所占有的概率。h → \to → 0是,F’(x)= f(x),也就是在x点(无穷小区段中)单位长的概率。
图形化表示为,
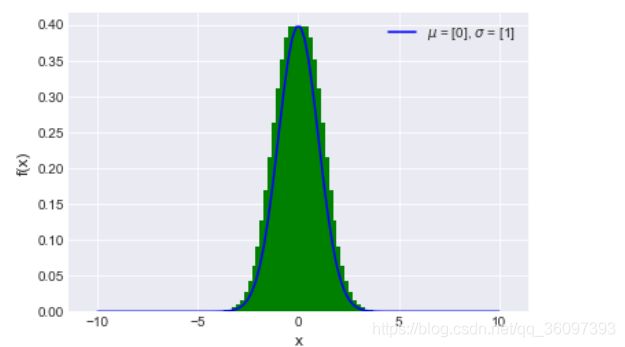
注意f(x)是x点(无穷小区段中)单位长的概率,是个极限值,值域不是[0,1]而是[0, + ∞ \infty ∞ ]。当 σ \sigma σ 很小的时候,类似一个冲击。
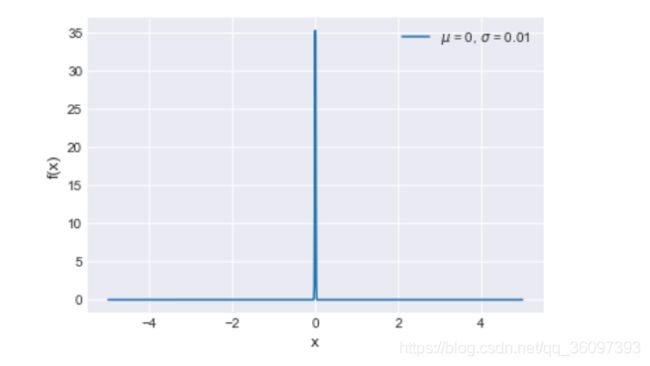
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as st
plt.style.use('seaborn-darkgrid')
x = np.linspace(-10, 10, 100)
mu = [0]
sigma = [1]
pdf = st.norm.pdf(x, mu, sigma)
plt.plot(x, pdf, color = "b",label=r'$\mu$ = {}, $\sigma$ = {}'.format(mu, sigma))
#plt.hist(x, pdf)
#plt.hist(pdf, range=[-5, 5], bins=100, histtype='stepfilled', normed=True)
plt.bar(x,pdf,color="g")
plt.xlabel('x', fontsize=12)
plt.ylabel('f(x)', fontsize=12)
plt.legend(loc=1)
plt.show()
函数表达式:
f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=2πσ1e−2σ2(x−μ)2
(陈希孺老师所著的《概率论与数理统计》值得一看)。
最大熵原理
高斯分布是根据最大熵原理得出来的一个分布。
多变量(联合)分布,
P(a ≤ X ≤ b, c ≤ Y ≤ d) =?
P(a1 ≤ X1 ≤ b1, ⋯ , ad ≤ Xd ≤ bd) =?
离散的联合概率分布
连续的联合概率分布

夸张的来讲,知道了联合概率分布,便知道了一切
多变量的高斯分布
μ ∈ R d \mu \in R^d μ∈Rd 是均值, ∑ ∈ R d ∗ d \sum \in R^{d*d} ∑∈Rd∗d是协方差,并且秩为1,因为 Σ = ( x − μ ) ( x − μ ) T \Sigma= (x-\mu)(x-\mu)^T Σ=(x−μ)(x−μ)T
p ( x 1 , x 2 , ⋯ , x d ) = 1 ( 2 π ) d ∣ Σ ∣ e − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) p(x_1,x_2,\cdots,x_d) = \frac{1}{\sqrt{(2\pi)^d|\Sigma|}}e^{-\frac{1}{2}}(x-\mu)^T\Sigma^{-1}(x-\mu) p(x1,x2,⋯,xd)=(2π)d∣Σ∣1e−21(x−μ)TΣ−1(x−μ)
1.2.3 独立和条件独立
参考西安交通大学孟得宇老师机器学习课
条件概率
P(X|Y ):给定Y事件为真的前提下X事件为真的概率
P ( X ∣ Y ) = P ( X , Y ) P ( Y ) P(X|Y) = \frac{P(X,Y)}{P(Y)} P(X∣Y)=P(Y)P(X,Y)
其中P(X,Y)联合概率密度给定,一切都可以算出来。
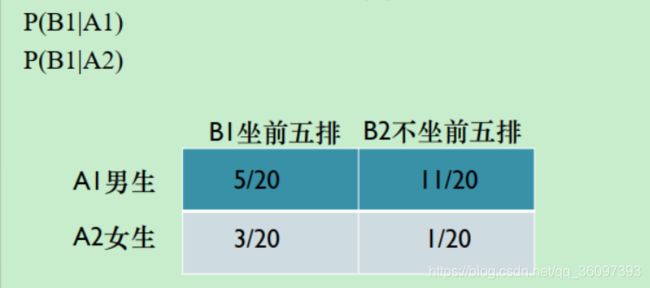
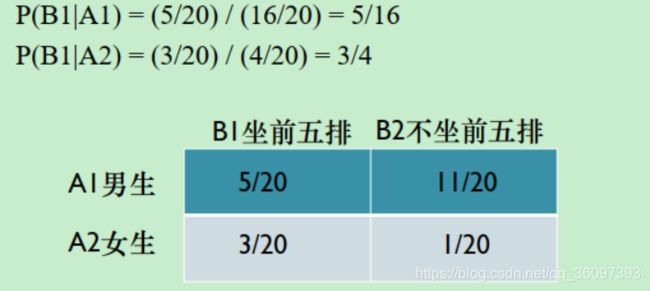
条件概率也是概率,符合概率公理, P ( Ω ) = 1 ; P ( A ) > 0 ; P(\Omega) = 1;P(A) > 0; P(Ω)=1;P(A)>0;以及不想交事件和的概率等于事件的概率之和。
独立性
P(X,Y) = P(X)P(Y) ; P(X|Y) =P(X)
含义:
- Y与X不包含互相的信息
- 观察到事件Y不能帮助预测X事件信息
- 观察到事件X不能帮助预测Y事件信息
例子:
连续投硬币,每次的结果的正反面不影响下一次的正反面。
条件独立
1.2 统计与概率研究问题的区别
参考机器学习(二十五)— 极大似然估计(MLE)、贝叶斯估计、最大后验概率估计(MAP)区别
概率研究的问题是,已知一个模型和参数,怎么去预测这个模型产生的结果的特性(例如均值,方差,协方差等等)。统计是,有一堆数据,要利用这堆数据去预测模型和参数。
概率是已知模型和参数,推数据。统计是已知数据,推模型和参数。
在统计里面,似然函数和概率函数却是两个不同的概念(其实也很相近就是了)。
对于这个函数:P(x|θ)。输入有两个:x表示某一个具体的数据;θ表示模型的参数。
如果θ是已知确定的,x是变量,这个函数叫做概率函数(probability function),它描述对于不同的样本点x,其出现概率是多少。
如果x是已知确定的,θ是变量,这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数,出现x这个样本点的概率是多少。
2 贝叶斯分类器
2.1贝叶斯公式
链式法则
( X , Y ) = P ( X ∣ Y ) P ( Y ) = P ( Y ∣ X ) P ( X ) (X, Y) = P(X|Y)P(Y) = P(Y|X)P(X) (X,Y)=P(X∣Y)P(Y)=P(Y∣X)P(X)
贝叶斯规则
P ( X ∣ Y ) = P ( Y ∣ X ) P ( X ) P ( Y ) P(X|Y) =\frac{P(Y|X)P(X)}{P(Y)} P(X∣Y)=P(Y)P(Y∣X)P(X)
不再单纯的根据以往的知识,或者从数据中统计得到的信息做决策,而是将两者结合。
2.2贝叶斯决策论
参考西瓜书和模式分类。
贝叶斯决策是概率框架上实施决策的基本方法,其出发点是利用概率的不同分类决策与相应的决策代价之间的定量折中。它做了如下假设,决策问题可以用概率的形式描述,并且假设所有有关的概率结构已知。
它的决策依据是规避风险。对于二分类,每次分类时的误差概率,
P ( e r r o r ∣ x ) = { p ( w 1 ∣ x ) 判 定 为 w 2 p ( w 1 ∣ x ) 判 定 为 w 1 P(error|x) = \left\{ \begin{aligned} &p(w_1 |x) \quad 判定为w2\\ &p(w_1 |x) \quad判定为w1\\ \end{aligned} \right. P(error∣x)={p(w1∣x)判定为w2p(w1∣x)判定为w1
当对于特征模式x,当判断为 w j w_j wj类是,我们会采取行动 a i a_i ai,,这时我们会有损失 λ i j \lambda_{ij} λij,一位做任何事都是有风险的,只不是大小的问题,这里的损失也不是什么贬义词。做这么一次决策,产生的损失为: R ( α i ∣ x ) = ∑ j = 1 c λ ( α i ∣ w j ) P ( w j ∣ x ) R(\alpha_i|x) = \sum\limits_{j=1}^c\lambda(\alpha_i|w_j)P(w_j|x) R(αi∣x)=j=1∑cλ(αi∣wj)P(wj∣x)
R ( α i ∣ x ) R(\alpha_i|x) R(αi∣x)条件风险,总风险为
R = ∫ R ( α ( x ) ∣ x ) p ( x ) d x R= \int R(\alpha(x)|x)p(x)dx R=∫R(α(x)∣x)p(x)dx
所以如果选择 α ( x ) \alpha(x) α(x)使得条件风险 R ( α i ∣ x ) R(\alpha_i|x) R(αi∣x)对每个x尽可能的小,那么那个风险就会被最小化。
此时, α ( x ) \alpha(x) α(x)为最优的分类器,很好的规避了风险,又是因为某些行动的代价胡总和损失太大,即使我们觉得x应该属于 w 1 w_1 w1,在贝叶斯分类器看来,将x判给 w 2 w_2 w2更能规避风险。再深究就有点博弈论的知识,等死?死国可乎?起义的概率很低,但在在天下雨,迟到的情况下,封建帝国主义制度下,起义对于生存的风险比等死的风险更低。
2.3MLE&MAP&贝叶斯估计
参考
频率学派还是贝叶斯学派?聊一聊机器学习中的MLE和MAP
详解最大似然估计(MLE)、最大后验概率估计(MAP),以及贝叶斯公式的理解
机器学习(二十五)— 极大似然估计(MLE)、贝叶斯估计、最大后验概率估计(MAP)区别
MLE是求使得数据集出现概率最大的参数,MAP和贝叶斯估计认为,参数是不确定了,随着数据的增多,我们对得到 θ \theta θ更有信心。公式化表示为: P ( D ∣ θ ) → P ( θ ∣ D ) P(D|\theta) \to P(\theta|D) P(D∣θ)→P(θ∣D),
抛硬币
对于抛硬币实验,估计正面向上的概率,先验选为beta分布,得出的结论是:
θ M L E = n z n z + n b \theta_{MLE} = \frac{n_z}{n_z+n_b} θMLE=nz+nbnz
θ M A P = β z + n z − 1 β z + n z + β B + n b − 2 \theta_{MAP} = \frac{\beta_z + n_z -1}{\beta_z + n_z + \beta_B +n_b -2} θMAP=βz+nz+βB+nb−2βz+nz−1
贝叶斯估计的结果:
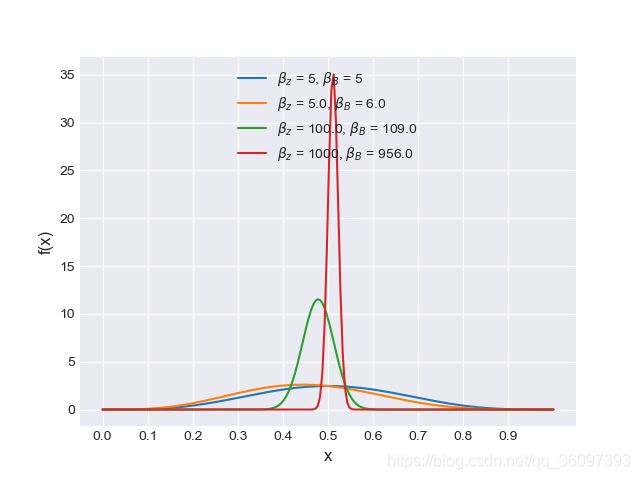
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as st
plt.style.use('seaborn-darkgrid')
x = np.linspace(0, 1, 200)
alphas = [5, 5., 100., 1000]
betas = [5, 6., 109., 956.]
for a, b in zip(alphas, betas):
pdf = st.beta.pdf(x, a, b)
plt.plot(x, pdf, label=r'$\beta_z$ = {}, $\beta_B$ = {}'.format(a, b))
plt.xlabel('x', fontsize=12)
plt.ylabel('f(x)', fontsize=12)
#plt.ylim(0, 10)
plt.xticks(np.arange(0, 1, 0.1))
plt.legend(loc=9)
plt.show()
程序实现–高斯分布
我们N(1,2)中随机采样得到有些数据点,利用这些数据进行参数估计。
MLE和MAP的结果:
使用两种不同的先验,并且MAP2的先验和数据本身很接近。
| 数据点个数 | MLE | MAP1 | MAP2 |
|---|---|---|---|
| 10 | [0.8058619 2.38176997] | [0.22830392 6.70833078] | [0.99762626 2.01023491] |
| 100 | [1.14863606 1.65963393] | [1.11702819 1.75930784] | [1.01753195 1.93319269] |
| 1000 | [1.06719326 2.00334822] | [1.0632993 2.01556288] | [1.03729344 2.00254846] |
| 10000 | [ 1.01803514 1.99994487] | [ 1.01766161 1.9979633] | [1.01669542 1.99994894] |
| 100000 | [ 1.00469426 -1.9969068 ] | [1.00466673 1.99702499] | [1.00466516 1.99691544] |
当数据点增加到1w时误差已经小于1%了。
贝叶斯估计结果为:
#!/usr/bin/env python
#!-*-coding:utf-8 -*-
'''
@version: python3.7
@author: ‘enshi‘
@license: Apache Licence
@contact: *******@qq.com
@site:
@software: PyCharm
@file: MLEMAP.py
@time: 11/14/2019 3:23 PM
'''
import numpy as np
from scipy.optimize import minimize
#theta= [u,sigma]
# def MLEF(X):
# fun = lambda theta: -np.multiply.reduce(1/(np.sqrt(2*np.pi)*theta[1]) * np.exp(-0.5*((X-theta[0])/(theta[1])+10E-9)**2))
# return fun
def MLENLL(X):
fun = lambda theta: -sum(-0.5*np.log(2*3.1415926*theta[1]**2) - 0.5/theta[1]**2*(X-theta[0])**2)
return fun
def MAPNLLG2(X):
fun = lambda theta: -sum(-0.5*np.log(2*3.1415926*theta[1]**2) - 0.5/theta[1]**2*(X-theta[0])**2) + (theta[1]-8)**2/2 + (theta[0]-0.1)**2/2
return fun
def MAPNLLG1(X):
fun = lambda theta: -sum(-0.5*np.log(2*3.1415926*theta[1]**2) - 0.5/theta[1]**2*(X-theta[0])**2) + (theta[1]-2)**2/0.01 + (theta[0]-1)**2/0.01
return fun
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def draw3D(X):
x = np.arange(0.5, 2.1, 0.01)
y = np.arange(1.5, 3.2, 0.01)
x,y = np.meshgrid(x, y)
#XY = np.concatenate((x,y),axis = 1)
z =np.zeros(x.shape)
length = x.shape[0] * x.shape[1]
for i in range( x.shape[0] ):
for j in range(x.shape[1]):
z[i,j] = MLENLL(X)(np.array([x[i,j],y[i,j]]).reshape(-1,1))
#z = np.array(z).reshape(x.shape)
fig = plt.figure()
ax = Axes3D(fig)
#ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=plt.cm.jet)
ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='rainbow')
plt.show()
nm = 8
#plt.contourf(x, y, z, nm, alpha=0.75, cmap='rainbow')
C1 = plt.contour(x, y, z, nm, colors='red')
plt.clabel(C1, inline=1, fontsize=10)
plt.show()
np.random.seed(1)
for i in range(5):
n = 10**(i+1)
X = 2*np.random.randn(n)+1
theta0 = np.array([0.9,0.9])
# res = minimize(MLEF(X),theta0,method='BFGS')
# print("data point:",n)
# print("x = ", res.x, '\t', "success", res.success, '\t',"function value", res.fun )
print("data point:", n)
# res = minimize(MLENLL(X), theta0, method='SLSQP')
print("MLE")
res = minimize(MLENLL(X), theta0, method='SLSQP')
print("x = ", res.x, '\t', "success", res.success, '\t', "function value", res.fun)
print("MAP")
res = minimize(MAPNLLG2(X), theta0, method='SLSQP')
print("x = ", res.x, '\t', "success", res.success, '\t', "function value", res.fun)
res = minimize(MAPNLLG1(X), theta0, method='SLSQP')
print("x = ", res.x, '\t', "success", res.success, '\t', "function value", res.fun)
#draw3D(X)
结论
- MLE,MAP和贝叶斯估计都是参数估计方法,都进行了iid(独立同分布)假设
- MLE和MAP都认为参数是一个确定的值,贝叶斯估计认为参数是一个分布。
- MLE和MAP把参数看成未知常数,MLE最大化似然,指利用数据提供的信息; MAP最大化后验概率实现,既利用数据提供的信息,也利用先验提供的信息。大数定理表明,在数据足够大的时候,频率等于概率,这时候来自于数据的知识足以得出准确的分布。
- 当先验为均匀分布时,极大似然估计和最大后验估计是等价的。因为均匀分布不提供任何信息。
- 通常情况下,贝叶斯估计的积分很难计算,但可以采取一些近似方法,如拉普拉斯和变分近似以及马尔科夫链蒙特卡洛抽样。
- 上升为频率学派与贝叶斯学派之争
- 贝叶斯学派: 在小数据时,你做的都是错的!
- 频域学派: 你太依赖先验,而且先验不同,结果也不同!
2.4 朴素贝叶斯
条件独立:
∀ x , y , z P ( X = x ∣ Y = y , Z = z ) = P ( X = x ∣ Z = z ) \forall x,y,z P(X=x | Y=y , Z= z) = P(X= x| Z =z) ∀x,y,zP(X=x∣Y=y,Z=z)=P(X=x∣Z=z)
等价于
P ( X , Y ∣ Z ) = P ( X ∣ Z ) P ( Y ∣ Z ) P(X,Y|Z) = P(X|Z)P(Y|Z) P(X,Y∣Z)=P(X∣Z)P(Y∣Z)
当Z事件发生时,X和Y独立。
当给定x时,他属于哪一类 ω \omega ω?
P ( ω ∣ x ) = P ( x ∣ ω ) P ( ω ) P ( x ) = P ( ω ) P ( x ) P ( x 1 , x 2 , . . . , x d ∣ ω ) P(\omega | x) = \frac{P(x|\omega)P(\omega)}{P(x)} = \frac{P(\omega)}{P(x)} P(x_1,x_2,...,x_d|\omega) P(ω∣x)=P(x)P(x∣ω)P(ω)=P(x)P(ω)P(x1,x2,...,xd∣ω) 联合概率有了条件性独立假设后,可以写成
P ( ω ∣ x ) = P ( ω ) P ( x ) P ( x 1 , x 2 , . . . , x d ∣ ω ) = P ( ω ) P ( x ) ∏ i = 1 d P ( x i ∣ ω ) P(\omega | x) = \frac{P(\omega)}{P(x)} P(x_1,x_2,...,x_d|\omega) = \frac{P(\omega)}{P(x)}\prod_{i=1}^dP(x_i|\omega) P(ω∣x)=P(x)P(ω)P(x1,x2,...,xd∣ω)=P(x)P(ω)i=1∏dP(xi∣ω)
再根据贝叶斯判定准则,找出最优的分类器。
2.4.1 垃圾邮件分类
垃圾邮件过滤–朴素贝叶斯 (Python)
给定语料库,我们根据预料中出现的所有的单词建立字典,基于特征 x = [ x 1 , x 2 , . . . x v o c L e n ] x= [x_1,x_2,...x_{vocLen}] x=[x1,x2,...xvocLen], x i x_i xi的取值为0或者1,出现则为1,不出现为0。基于语料库,我们可以得出
(1)先验概率,P(Y)
(2) 类条件概率,在垃圾邮件和正常邮件中,每个词出现的概率P(W|Y)。
我们假设将邮件错分为垃圾邮件或者错分为正常邮件的损失相同.
当我们输入一个邮件时,先得到特征x,根据
P ( Y ∣ x ) = P ( Y ) P ( x ) ∏ i = 1 d P ( x i ∣ Y ) P(Y | x) = \frac{P(Y)}{P(x)}\prod_{i=1}^dP(x_i|Y) P(Y∣x)=P(x)P(Y)i=1∏dP(xi∣Y)
分别算出邮件为垃圾邮件和正常邮件的概率,那个概率大就是判别为哪一类,这是朴素贝叶斯的判断过程。
程序为:
#!/usr/bin/env python
#!-*-coding:utf-8 -*-
'''
@version: python3.7
@author: ‘enshi‘
@license: Apache Licence
@contact: *******@qq.com
@site:
@software: PyCharm
@file: email.py
@time: 11/21/2019 4:13 PM
'''
import numpy as np
def create_vocab_list(dataset):
# dataset 包含了多条留言的文本,每一条留言为一个列表
vocabset = set([])
for document in dataset:
vocabset = vocabset | set(document)
return list(vocabset)
def wordsToVector(vocabset, inputset):
# vocabset 是词汇表, inputset 为要转化为向量的文本
vector = [0]*len(vocabset)
for word in inputset:
if word in vocabset:
vector[vocabset.index(word)] = 1
else:
print("The word: {} is not in my Vocabulary.".format(word))
return vector
def traing_bayes(trainset, trainCategory):
"""sovle the conditional probility"""
# trainCategory 是标记为负类和正类的向量
num_train = len(trainset)
# 获取训练集的数量,其中训练集是由文本向量组成
num_vocab = len(trainset[0])
# 由于训练集中的每个元素都是文本向量,即包含了整个词汇表
pAbusive = sum(trainCategory) / num_train
# 计算负类的概率,负类的数量除以训练集的数目
pnorm_vector = np.ones(num_vocab)
# 每个词汇出现在正类中的概率组成的向量
pabu_vector = np.ones(num_vocab)
# 每个词汇出现在负类中的概率组成的向量
pnorm_denom = num_vocab
# 正类中词汇的数目
pabu_denom = num_vocab
# 负类中词汇的数目
for i in range(num_train):
if trainCategory[i] == 1:
pabu_vector += trainset[i]
pabu_denom += sum(trainset[i])
else:
pnorm_vector += trainset[i]
pnorm_denom += sum(trainset[i])
pnorm_vector = np.log(pnorm_vector / pnorm_denom)
pabu_vector = np.log(pabu_vector / pabu_denom)
return pnorm_vector, pabu_vector, pAbusive
def classify(testVector, pnorm_vector, pabu_vector, pabusive):
# 先将测试文本转化为向量
pnorm = sum(testVector*pnorm_vector) + np.log(1 - pabusive)
# 计算测试文本为正类的概率
pabu = sum(testVector*pabu_vector) + np.log(pabusive)
# 计算测试文本为负类的概率
if pabu > pnorm:
return 1
else:
return 0
def load_data_set():
posting_list = [
['my', 'dog', 'has', 'flea', 'problem', 'help', 'please'],
['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
['stop', 'posting', 'stupid', 'worthless', 'garbage'],
['mr', 'licks', 'ate', 'ny', 'steak', 'how', 'to', 'stop', 'him'],
['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']
]
labels = [0, 1, 0, 1, 0, 1]
return posting_list,labels
def test_bayes():
posts_list, classes_list = load_data_set()
vocab_list = create_vocab_list(posts_list)
trainset = []
for post in posts_list:
trainset.append(wordsToVector(vocab_list, post))
pnorm_vector, pabu_vector, pAbusive = traing_bayes(trainset, classes_list)
testEntry = ['love', 'my', 'dalmation']
testVector = np.array(wordsToVector(vocab_list, testEntry))
print(testEntry, "classified as: {}".format(classify(testVector, pnorm_vector, pabu_vector, pAbusive)))
testEntry = ['stupid', 'garbage']
testVector = np.array(wordsToVector(vocab_list, testEntry))
print(testEntry, "classified as: {}".format(classify(testVector, pnorm_vector, pabu_vector, pAbusive)))
# 结果如下:
# ['love', 'my', 'dalmation'] classified as: 0
# ['stupid', 'garbage'] classified as: 1
if __name__ == '__main__':
test_bayes()
结果
2.5 半朴素贝叶斯
2.6 贝叶斯网
3. Questions and Answers
- 联合概率分布为什么那么重要?
对于贝叶斯公式 P ( Y ∣ X ) = P ( X , Y ) P ( X ) P(Y|X) = \frac{P(X,Y)}{P(X)} P(Y∣X)=P(X)P(X,Y)知道了联合概率,便可以得到先验分布P(X),进而得到后延概率P(Y|X) .
3 贝叶斯定理的含义?
结合先验知识和观测的数据得到后验概率 - MLE与MAP各自的特点与本质
MLE和MAP都是参数估计,都假设独立同分布,把参数看成未知常数,MLE最大化似然函数,指利用数据提供的信息; MAP最大化后验概率实现,既利用数据提供的信息,也利用先验提供的信息 - 贝叶斯分类器的基本概念与原理
基本概念:基于贝叶斯公式,利用概率和误判损失来选择最优的分类器,最小化风险。
基本原理:根据先验概率和类条件概率得后验概率,利用后验概率和相应的决策代价得到最小化风险的最优分类器。 - NB(朴素贝叶斯)方法的:假设,动机,怎样训练和预测, MAP重要性
假设:条件独立
动机:想从有限的样本中得到联合概率分布,从而能使用贝叶斯分类器进行分类。
怎么样训练:根据样本算出先验概率和各个属性对应的类条件概率
怎么样预测: 根据先验概率,类体概率和贝叶斯公式,计算后验概率,比较后验概率的大小,确定最优值。 - 文本分类与BoW原理
文本分类: 给定文档p(可能含有标题t),将文档分类为n个类别中的一个或多个
BoW原理:不管字的排序,只管出现次数 - 高斯NB原理
处理连续分布时,假设类条件概率中每个属性属于高斯分布,通过参数估计计算均值和方差。结合所得到的先验概率,计算后验概率,比较大小。 - 若有少数Xi相关,能否改造NB方法?
将联合条件概率密度,按照少量相关的形式来计算。
参考资源
西安交通大学孟得宇老师机器学习课
A Sampling Of Monte Carlo Methods
Pymc3
应该如何理解概率分布函数和概率密度函数?
如何通俗理解 beta 分布?
文本分类概述
解开贝叶斯黑暗魔法:通俗理解贝叶斯线性回归