K-近邻算法
K 近邻法
K 近邻法(k-nearest neighbors,KNN)是一种基本分类与回归方法,于 1968 年由 Cover 和 Hart 提出。
【过程】:假设给定一个训练数据集,其中的实例类别已定。分类时,对新的实例,根据其 K 个最近训练实例的类别,通过多数表决等方式进行预测。
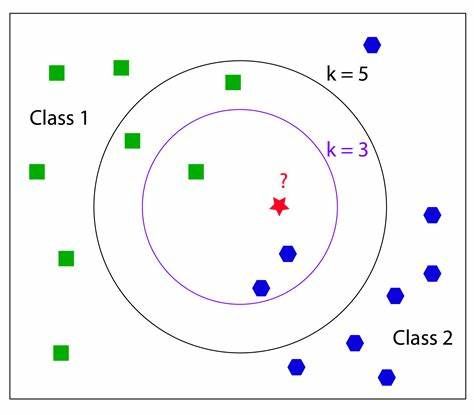
如上图所示,绿色方块 w1、蓝色六角星 w2 分别代表训练集中的两个类别。图中与红色五角星最相近的 3(k=3)个点如图中内层圈,很明显与 红色五角星最相近的 3 个点中最多的类标为 w2,因此 KNN 算法将红色五角星的类别预测为 w2。当 k = 5 时,可以看到 KNN 算法将红色五角星的类别预测为 w1。
从上述案例中可以发现:新实例的类别判断取决于 K 值的选择;除此之外,实例之间的距离计算方式以及分类决策规则都会对最终的分类结果产生影响。
【三个基本要素】:
- K 值的选择
- 距离度量
- 分类决策规则
先介绍统计学中 K 近邻算法的实现,然后再用 Python 语言真正意义上实现 K-近邻算法。
K 近邻算法
给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的 K 个实例,这 K 个实例的多数属于某个类,就把该输入实例分为这个类。
【算法】:K 近邻法。
- 输入:实例特征向量 x、训练数据集
T = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) , x i ∈ χ ⊆ R n , y i ∈ Y = c 1 , c 2 , ⋯ , c k T = {(x_1, y_1), (x_2, y_2), ..., (x_N, y_N)}, \quad x_i \in \chi \subseteq R^n, \quad y_i \in Y = {c_1, c_2, \cdots, c_k} T=(x1,y1),(x2,y2),...,(xN,yN),xi∈χ⊆Rn,yi∈Y=c1,c2,⋯,ck
其中,x 为实例的特征向量,y 为实例的类别; - 输出:实例 x 所属的类 y。
- 过程:
- 根据给定的距离度量,在训练集 T 中找出与 x 最邻近的 k 个点,涵盖这 k 个点的 x 的邻域记作 N k ( x ) N_k(x) Nk(x)。
- 在 N k ( x ) N_k(x) Nk(x) 中根据分类决策规则(如多数表决)决定 x 的类别 y。
y = a r g m a x c j ∑ x i ∈ N k ( x ) I ( y i = c j ) , i = 1 , 2 , . . . , N ; j = 1 , 2 , . . . , K y = argmax_{c_j} \sum_{x_i \in N_k(x)}I(y_i = c_j), i = 1,2,...,N; j = 1,2,...,K y=argmaxcjxi∈Nk(x)∑I(yi=cj),i=1,2,...,N;j=1,2,...,K
上式中,I 为指示函数,即当 y i = c j y_i = c_j yi=cj 时 I 为 1,否则 I 为 0。
【特殊情况】:k = 1 的情形,称为最近邻算法,对于输入的实例点(特征向量)x,最近邻法将训练数据集中与 x 最邻近点的类作为 x 的类。
【说明】:K 近邻法不具有显式的学习过程,实际上是利用训练数据集对特征向量空间进行划分,并作为其分类的“模型”。从算法实现的过程中也能看出,KNN 的训练过程实际上仅仅只是保存训练数据,然后在预测过程中用来计算与预测点的距离。
【缺陷】:K-近邻算法是基于实例的学习,使用算法时必须有接近实际数据的训练样本数据。
- K-近邻算法必须保存全部数据集,如果训练数据集很大,必须使用大量的存储空间。此外,由于必须对数据集中的每个数据计算距离值,实际使用时可能非常耗时。
- K-近邻算法无法给出任何数据的基础结构信息,因此我们无法知晓平均实例样本和典型实例样本具有什么特征。
K 近邻模型
K 近邻法使用的模型实际上对应于特征空间的划分。模型由三个基本要素——距离度量、K 值的选择和分类决策规则决定。
模型
K 近邻法中,当训练集、距离度量(如欧氏距离)、k 值及分类决策规则(如多数表决)确定后,对于任何一个新的输入实例,它所属的类唯一地确定。这相当于根据上述要素将特征空间划分为一些子空间,确定子空间里的每个点所属的类。
特征空间中,对每个训练实例点 x i x_i xi,距离该点比其他点更近的所有点组成一个区域,叫作单元(cell)。每个训练实例点拥有一个单元,所有训练实例点的单元构成对特征空间的一个划分。最近邻法将实例 x i x_i xi 的类 y i y_i yi 作为其单元中所有点的类标记(class label)。这样,每个单元的实例点的类别是确定的。
距离度量
特征空间中两个实例点的距离是两个实例点相似程度的反映。
K 近邻模型的特征空间一般是 n 维实数向量空间 R n R^n Rn,使用的距离是欧氏距离,但也可以是更一般的 L p L_p Lp 距离或 Minkowski 距离
设特征空间 χ \chi χ 是 n 维实数向量空间 R n R^n Rn, x i , x j ∈ χ , x i = ( x i ( 1 ) , x i ( 2 ) , . . . , x i ( n ) ) T , x j = ( x j ( 1 ) , x j ( 2 ) , . . . , x j ( n ) ) T x_i, x_j \in \chi, x_i=(x_i^{(1)}, x_i^{(2)}, ..., x_i^{(n)})^T, x_j = (x_j^{(1)}, x_j^{(2)}, ..., x_j^{(n)})^T xi,xj∈χ,xi=(xi(1),xi(2),...,xi(n))T,xj=(xj(1),xj(2),...,xj(n))T, x i , x j x_i, x_j xi,xj 的 L p L_p Lp 距离定义为:
L p ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ p ) 1 p L_p(x_i, x_j) = (\sum_{l=1}^{n}|{x_i^{(l)} - x_j^{(l)}|^p})^{\frac{1}{p}} Lp(xi,xj)=(l=1∑n∣xi(l)−xj(l)∣p)p1
这里 p ≥ 1 p \geq 1 p≥1,当 p = 2 时,称为欧式距离(Euclidean distance),即
L 2 ( x i , x j ) = ( ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ 2 ) 1 2 L_2(x_i, x_j) = (\sum_{l=1}^{n}|{x_i^{(l)} - x_j^{(l)}|^2})^{\frac{1}{2}} L2(xi,xj)=(l=1∑n∣xi(l)−xj(l)∣2)21
当 p = 1 时,称为曼哈顿距离(Manhattan distance),或城市街区距离(cityblock distance)即
L 1 ( x i , x j ) = ∑ l = 1 n ∣ x i ( l ) − x j ( l ) ∣ L_1(x_i, x_j) = \sum_{l=1}^{n}|{x_i^{(l)} - x_j^{(l)}|} L1(xi,xj)=l=1∑n∣xi(l)−xj(l)∣
当 p = 无穷时,称为切比雪夫距离(Chebyshev distance),它是各个坐标距离的最大值,即
L ∞ ( x i , x j ) = m a x l ∣ x i ( l ) − x j ( l ) ∣ L_\infty(x_i, x_j) = max_l|{x_i^{(l)} - x_j^{(l)}}| L∞(xi,xj)=maxl∣xi(l)−xj(l)∣
【代码实现】:scipy.spatial.distance 包中的 cdist 方法。
>>> from scipy.spatial.distance import cdist
>>> x1, x2 = [3, 2], [1, 4]
>>> # 欧氏距离
... cdist(x1, x2, 'euclidean')
array([[2.82842712]])
>>> # 曼哈顿距离
... cdist(x1, x2, 'cityblock')
array([[4.]])
>>> # 切比雪夫距离
... cdist(x1, x2, 'chebyshev')
array([[2.]])
【代码实现】:numpy.linalg.norm 方法。
>>> import numpy as np
>>> x1, x2 = np.array([3, 2]), np.array([1, 4])
>>> # 欧式距离
... np.linalg.norm(x1 - x2, 2)
2.8284271247461903
>>> # 曼哈顿距离
... np.linalg.norm(x1 - x2, 1)
4.0
>>> # 切比雪夫距离
... np.linalg.norm(x1 - x2, np.inf)
2.0
不同的距离度量所确定的最近邻点是不同的。
【示例】:已知二维空间的 3 个点 x 1 = ( 1 , 1 ) T , x 2 = ( 5 , 1 ) T , x 3 = ( 4 , 4 ) T x_1 = (1, 1)^T, x_2 = (5, 1)^T, x_3 = (4, 4)^T x1=(1,1)T,x2=(5,1)T,x3=(4,4)T,试求在 p 取不同值时, L p L_p Lp 距离下 x 1 x_1 x1 的最近邻点。
【答】:因为 x1 和 x2 自由第二维上值不同,所以不管 p 取何值,Lp(x1, x2) = 4。而 L1(x1, x3) = 6,L2(x1, x3) = 4.24,L3(x1, x3) = 3.78,L4(x1, x3) = 3.57,可得到如下结论。
- p <= 2:x2 是 x1 的最近邻点。
- p > 2:x3 是 x1 的最近邻点。
K 值的选择
K 值的选择会对 K 近邻法的结果产生重大影响。
【K 值较小】:相当于用较小邻域中的训练实例进行预测,模型的训练误差会减小,只有与输入实例较近的训练实例才会对预测结果起作用。
- 缺点:模型的泛化误差会增大,预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声,预测就会出错。换句话说,K 值的减小就意味着整体模型变得复杂,容易发生过拟合。
【K 值较大】:相当于用较大邻域中的训练实例进行预测。可以减少模型的泛化误差。
- 缺点:训练误差会增大。这时,与输入实例较远的训练实例也会对预测起作用,使预测发生错误。K 值的增大意味着整体的模型变得简单。
【K = N】:无论输入实例是什么,都将简单地预测它属于在训练实例中最多的类。此时,模型过于简单,完全忽略训练实例中的大量有用信息。
在实际应用中,K 值一般取一个比较小的数值(sklearn 中的 KNeighborsClassifier 默认 k 值为 5)、通常采用交叉验证法来选取最优的 K 值。
分类决策规则
K 近邻法中的分类决策规则往往是多数表决,即由输入实例的 K 个邻近训练实例中的多数类决定输入实例的类。
例如,当前实例的 5 个邻近训练实例中有 3 个属于正类,2 个属于负类,那么该实例最终被预测为正类。
【多数表决规则(majority voting rule)】:如果分类的损失函数为 0-1 损失函数,分类函数为
f : R n → { c 1 , c 2 , . . . , c k } f: R^n \rightarrow \{c_1, c_2, ..., c_k\} f:Rn→{c1,c2,...,ck}
那么,误分类的概率是
P ( Y ̸ = f ( X ) ) = 1 − P ( Y = f ( X ) ) P(Y \not= f(X)) = 1 - P(Y=f(X)) P(Y̸=f(X))=1−P(Y=f(X))
对给定实例 x ∈ χ x \in \chi x∈χ,其最近邻的 k 个训练实例点构成集合 N k ( x ) N_k(x) Nk(x)。如果涵盖 N k ( x ) N_k(x) Nk(x) 的区域的类别是 c j c_j cj,那么误分类率是
1 k ∑ x i ∈ N k ( x ) I ( y i ≠ c j ) = 1 − 1 k ∑ x i ∈ N k ( x ) I ( y i = c j ) \frac{1}{k} \sum_{x_i \in N_k(x)} I(y_i \neq c_j) = 1 - \frac{1}{k} \sum_{x_i \in N_k(x)}I(y_i = c_j) k1xi∈Nk(x)∑I(yi̸=cj)=1−k1xi∈Nk(x)∑I(yi=cj)
要使误分类率最小即经验风险最小,就要使 ∑ x i ∈ N k ( x ) I ( y i = c j ) \sum_{x_i \in N_k(x)}I(y_i = c_j) ∑xi∈Nk(x)I(yi=cj) 最大,所以多数表决规则等价于经验风险最小化。
K 近邻法实现
K 近邻法共有两种实现方式:
- 线性扫描(linear scan):计算输入实例与每一个训练实例的距离。优点是简单易实现,但训练集很大时,计算非常耗时,不可行。
- kd 树:利用 kd 树可以省去对大部分数据点的搜索,从而减少搜索的计算量。
线性扫描
【思路】:计算目标点与已有的全部点之间的距离,然后从中选择距离最短的 k 个近邻点,并获得这些点的类别信息。最后根据这些点的类别信息判断目标点的类别。
【前置准备】:
import numpy as np
from scipy.spatial.distance import cdist
class KNN:
def __init__(self, k=5, dist_method='euclidean', vote_method='count'):
self.k = k
self.dist_method = dist_method
self.vote_method = vote_method
def _get_distance(self, XA, XB, method='euclidean'):
method_list = ['euclidean', 'city_block', 'chebyshev']
if method not in method_list:
raise Exception('The distance method not exist!')
return cdist(XA, [XB], method)
获取 k 近邻点
def _find_k_nearest(self, x, y, target):
dists = self._get_distance(x, target)
nearests = sorted([[dists[i], y[i]] for i in range(x.shape[0])], key=lambda data:data[0])
return np.array(nearests[:self.k])
【说明】:
- 计算目标向量与所有特征向量的距离。
dists = self._get_distance(x, target)
- 整合成二维数组形式,第一列为距离,第二列为类别。
[[dists[i], y[i]] for i in range(x.shape[0])]
- 对整合后的二维数组按照距离进行升序排序。
sorted([[dists[i], y[i]] for i in range(x.shape[0])], key=lambda data:data[0])
- 返回前 k 条记录(包括距离以及类别信息)。
return np.array(nearests[:self.k])
根据分类决策规则确定类别
def _vote(self, nearests, method='count'):
labels = nearests[:, 1].tolist()
return sorted([(labels.count(label), label) for label in set(labels)])[-1][1]
【说明】:
- 首先,将所有的分类信息从 nearests 数组中抽取出来。
labels = nearests[:, 1].tolist()
- 统计每个类别的数目。
[(labels.count(label), label) for label in set(labels)]
- 对统计结果进行排序。
sorted([(labels.count(i), i) for i in set(labels)])
[(2, 2), (3, 1)]
- 返回数目最大的类别。
return sorted([(labels.count(i), i) for i in set(labels)])[-1][1]
【问题】:如果数目相同会怎么样?
【回答】:每个算法都有它自己的特征偏好,在上述代码中可以看出,sorted() 方法对类别进行升序排序,因此,在数目相同的情况下,优先选择排序较大的类别。假设,类别 1 和类别 2 的数目相同,则优先选择类别 2。
除了统计各分类的数目之外,也可以基于距离远近来增加“投票”的权值,也就是说,离目标点越近的点对目标点类别的影响越大。
def _vote(self, nearests, method='count'):
labels = {}
dist_mean = np.mean(nearests[:, 0])
for data in nearests:
dist = dist_mean / data[0]
label = data[1]
if label not in labels:
labels[label] = dist
else:
labels[label] += dist
return sorted([(labels[label], label) for label in set(labels)])[-1][1]
【说明】:
- 初始化 labels 字典以及计算平均距离。
labels = {}
dist_mean = np.mean(nearests[:, 0])
- 循环遍历 nearests 数组,统计各个类别的权值之和。
for data in nearests:
dist = dist_mean / data[0]
label = data[1]
if label not in labels:
labels[label] = dist
else:
labels[label] += dist
- 最后,比较各个分类总权值的大小,确定最终的分类。
return sorted([(labels[label], label) for label in set(labels)])[-1][1]
采用“总平均距离 / 各近邻点距离”是为了让最后各分类所得的总权值不至于太小(如果分子都为 1,所得的权值过小)。
最后,将两种分类决策规则整合到一块,完整的代码如下:
def _vote(self, nearests):
if self.vote_method == 'count':
labels = nearests[:, 1].tolist()
return sorted([(labels.count(label), label) for label in set(labels)])[-1][1]
elif self.vote_method == 'distance':
labels = {}
dist_mean = np.mean(nearests[:, 0])
for data in nearests:
dist = dist_mean / data[0]
label = data[1]
if label not in labels:
labels[label] = dist
else:
labels[label] += dist
return sorted([(labels[label], label) for label in set(labels)])[-1][1]
完整代码
class KNN:
def __init__(self, k=5, dist_method='euclidean', vote_method='count'):
if k <= 0:
raise Exception('The param k is not less then or equal to zero!')
dist_method_list = ['euclidean', 'city_block', 'chebyshev']
if dist_method not in dist_method_list:
raise Exception('The distance method not exist!')
vote_method_list = ['count', 'distance']
if vote_method not in vote_method_list:
raise Exception('The vote method not exist!')
self.k = k
self.dist_method = dist_method
self.vote_method = vote_method
def set_k(self, k):
if k <= 0:
raise Exception('The param k is not less then or equal to zero!')
self.k = k
def set_dist_method(self, dist_method):
dist_method_list = ['euclidean', 'city_block', 'chebyshev']
if dist_method not in dist_method_list:
raise Exception('The distance method not exist!')
self.dist_method = dist_method
def set_vote_method(self, vote_method):
vote_method_list = ['count', 'distance']
if vote_method not in vote_method_list:
raise Exception('The vote method not exist!')
self.vote_method = vote_method
def _get_distance(self, XA, XB, method='euclidean'):
return cdist(XA, [XB], method)
def _find_k_nearest(self, x, y, target):
dists = self._get_distance(x, target)
nearests = sorted([[dists[i], y[i]] for i in range(x.shape[0])], key=lambda data:data[0])
return np.array(nearests[:self.k])
def _vote(self, nearests):
if self.vote_method == 'count':
labels = nearests[:, 1].tolist()
return sorted([(labels.count(label), label) for label in set(labels)])[-1][1]
elif self.vote_method == 'distance':
labels = {}
dist_mean = np.mean(nearests[:, 0])
for data in nearests:
dist = dist_mean / data[0]
label = data[1]
if label not in labels:
labels[label] = dist
else:
labels[label] += dist
return sorted([(labels[label], label) for label in set(labels)])[-1][1]
def fit(self, x, y):
self.x = x
self.y = y
def predict(self, target):
nearests = self._find_k_nearest(self.x, self.y, target)
label = self._vote(nearests)
return label
《机器学习实战》
再来看一下《机器学习实战》这本书是如何实现 K 近邻算法,以及 K 近邻算法的应用。
【实施过程】:对未知类别属性的数据集中的每个点依次执行以下操作。
- 计算已知类别数据集中的点与当前点之间的距离。
- 按照距离递增次序排序。
- 选取与当前点距离最小的 k 个点。
- 确定前 k 个点所在类别的出现频率。
- 返回前 k 个点出现频率最高的类别作为当前点的预测分类。
【程序代码】:
from numpy import *
import operator
def classify0(inX, dataSet, labels, k):
"""
k-近邻算法
:param inX: 输入向量
:param dataSet: 训练样本集
:param labels: 标签向量
:param k: 选择最近邻居的数目
:return: 输入向量对应的标签
"""
# 距离计算
dataSetSize = dataSet.shape[0]
diffMat = tile(inX, (dataSetSize, 1)) - dataSet
sqDiffMat = diffMat ** 2
sqDistances = sqDiffMat.sum(axis=1)
distances = sqDistances ** 0.5
# 距离升序排序
sortedDistIndicies = distances.argsort()
# 选取与当前点距离最小 k 个点所在类别的出现频率
classCount = {}
for i in range(k):
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
sortedClassCount = sorted(classCount.iteritems(),
key=operator.itemgetter(1),
reverse=True)
# 返回前 K 个点出现频率最高的类别
return sortedClassCount[0][0]
【注意】:在 Python 3.x 版本中,dict 对象不存在 iteritems() 方法,需要用 items() 来替代。tile 函数的用法请参考官网文档 传送门。
示例:使用 K-近邻算法改进约会网站的配对效果
【传送门】:使用 K-近邻算法改进约会网站的配对效果
示例:手写识别系统
【传送门】:手写识别系统
K 近邻法的实现:kd 树
【主要考虑问题】:如何对训练数据进行快速 K 近邻搜索,尤其是在特征空间的维数大、训练数据容量大时。
构造 kd 树
kd 树是一种对 k 维空间中的实例点进行存储以便对齐进行快速检索的树形数据结构。
【说明】:
- kd 树是二叉树,表示对 k 维空间的一个划分(partition)。
- 构造 kd 树相当于不断地用垂直于坐标轴的超平面将 k 维空间切分,构成一系列的 k 维超矩形区域。
- kd 树的每个结点对应于一个 k 维超矩形区域。
【方法】:
- 构造根结点,使根结点对应于 k 维空间中包含所有实例点的超矩形区域。
- 在超矩形区域(结点)上选择一个坐标轴和在此坐标轴上的一个切分店,确定一个超平面,这个超平面通过选定的切分店并垂直于选定的坐标轴,将当前超矩形区域切分为左右两个子区域(子结点)。这时,实例被分到两个子区域。
- 递归第二步操作,不断地对 k 维空间进行切分,生成子结点。
- 直到子区域内没有实例时终止(终止时的结点为叶结点)。在此过程中,将实例保存在相应的结点上。
通常,依次选择坐标轴对空间切分,选择训练实例点在选定坐标轴上的中位数(median)为切分点,这样得到的 kd 树是平衡的。需要注意的是,平衡的 kd 树搜索时的效率未必是最优的。
【算法】:构造平衡 kd 树
- 输入:k 维空间数据集 T = { x 1 , x 2 , . . . , x N } T = \{x_1, x_2, ..., x_N\} T={x1,x2,...,xN},其中 x i = ( x ( 1 ) , x ( 2 ) , . . . , x ( k ) ) T , i = 1 , 2 , . . . , N x_i = (x^{(1)}, x^{(2)}, ..., x^{(k)})^T, i=1,2,...,N xi=(x(1),x(2),...,x(k))T,i=1,2,...,N;
- 输出:kd 树。
- 过程:
- 开始:构造根结点,根结点对应于包含 T 的 k 维空间的超矩形区域。
- 选择 x ( 1 ) x^{(1)} x(1) 为坐标轴,以 T 中所有实例的 x ( 1 ) x^{(1)} x(1) 坐标的中位数为切分点,将根结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴 x ( 1 ) x^{(1)} x(1) 垂直的超平面实现。
- 由根结点生成深度为 1 的左、右子结点;左子结点对应坐标 x ( 1 ) x^{(1)} x(1) 小于切分点的子区域,右子结点对应于坐标 x ( 1 ) x^{(1)} x(1) 大于切分点的子区域。
- 将落在切分超平面上的实例点保存在根结点。
- 重复:对深度为 j 的结点,选择 x ( l ) x^{(l)} x(l) 为切分的坐标轴,l = j(mod k) + 1,以该结点的区域中所有示例的 x ( l ) x^{(l)} x(l) 坐标的中位数为切分点,将该结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴 x ( l ) x^{(l)} x(l) 垂直的超平面实现。
- 由该结点生成深度为 j + 1 的左、右子结点:左子结点对应坐标 x ( l ) x^{(l)} x(l) 小于切分点的子区域,右子结点对应坐标 x ( l ) x^{(l)} x(l) 大于切分点的子区域。
- 将落在切分超平面上的实例点保存在该结点。
- 直到两个子区域没有实例存在时停止,从而形成 kd 树的区域划分。
搜索 kd 树
给定一个目标点,搜索其最近邻。首先找到包含目标点的叶结点,然后从该叶结点出发,依次回退到父结点。不断查找与目标点最邻近的结点,当确定不可能存在更近的结点时终止。这样搜索就被限制在空间的局部区域上,效率大为提高。
包含目标点的叶结点对应包含目标点的最小超矩形区域,以此叶结点的实例点作为当前最近点。目标点的最近邻一定在以目标点为中心并通过当前最近点的超球体的内部。然后返回当前结点的父结点,如果父结点的另一子结点的超矩形区域与超球体相交,那么在相交的区域内寻找与目标点更近的实例点。如果存在这样的点,将此点作为新的当前最近点。算法转到更上一级的父结点,继续上述过程。如果父结点的另一子结点的超矩形区域与超球体不相交,或不存在比当前更近点更近的点,则停止搜索。
【算法】:用 kd 树的最近邻搜索
- 输入:已构造的 kd 树,目标点 x。
- 输出:x 的最近邻。
- 过程:
- 在 kd 树中找出包含目标点 x 的叶结点:从根结点出发,递归地向下访问 kd 树。若目标点 x 当前维的坐标小于切分点的坐标,则移动到左子结点,否则移动到右子结点。直到子结点为叶结点为止。
- 以此叶结点为“当前最近点”。
- 递归地向上回退,在每个结点进行以下操作:
- 如果该结点保存的实例点比的最近点距离目标点更近,则以该实例点为“当前最近点”。
- 当前最近点一定存在与该结点一个子结点对应的区域。检查该子结点的父结点的另一子结点对应的区域是否有更近的点。具体地,检查另一子结点对应的区域是否与以目标点为球心、以目标点与“当前最近点”间的距离为半径的超球体相交。
- 如果相交,可能在另一个子结点对应的区域内存在距目标点更近的点,移动到另一个子结点。接着,递归地进行最近邻搜索。
- 如果不相交,向上回退。
- 当回退到根结点时,搜索结束。最后的“当前最近点”即为 x 的最近邻点。
【说明】:如果实例点是随机分布的,kd 树搜索的平均计算复杂度是 O(logN),这里 N 是训练实例数。kd 树更适用于训练实例数远大于空间维数时的 k 近邻搜索。当空间维数接近训练实例数时,它的效率会迅速下降,几乎接近线性扫描。
上面所讲的关于 Kd 树的内容属于统计学方面的实现,不容易理解,可以查看这篇文章 《k-d tree 算法实现》
代码实现
第一步,准备数据。
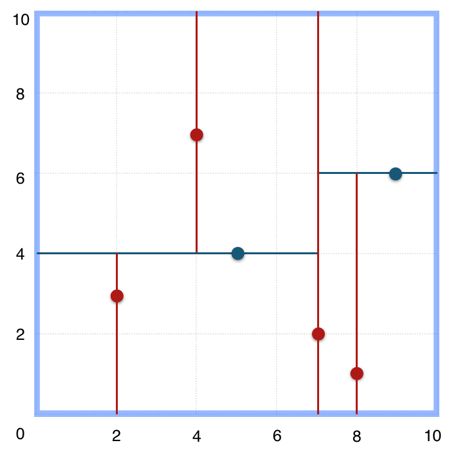
# data.csv 文件
2, 3, 1
5, 4, 1
9, 6, 2
4, 7, 1
8, 1, 2
7, 2, 1
【说明】:
- 前两列数据是实例的特征向量 x,最后一列数据是实例的类别。
- 为什么要使用这数据?上述数据在 KNN 的各类书籍和资料中经常出现(在原有的前两列基础上添加了最后一列),为了方便理解以及结合其他资料加深思考,因此以该数据作为示例。
第二步,读取数据。
from pandas import read_csv
data = read_csv('./data.csv', names=['x1', 'x2', 'label'])
array = data.values
x = array[:, 0:2]
y = array[:, 2]
第三步,创建 kd 树节点。
class KdNode(object):
data: 0
split: 0
parent: None
left: None
right: None
type: None
def __init__(self, data, split, type):
self.data, self.split, self.type = data, split, type
self.flag = False
第四步,构造 kd 树。
def create_kd_tree(self, data):
if len(data) == 0:
return None
# 获取方差最大的维度
squared = np.var(data, 0)
split = np.argmax(squared[:-1])
# 对数据进行排序
ind = np.argsort(data, 0)
data = data[ind[:, split]]
# 计算中位数并划分数据
middle_index = int(np.floor(len(data) / 2))
data_left, data_middle, data_right = np.vsplit(data, (middle_index, middle_index + 1))
kd_point = KdNode(data_middle, split, int(data_middle[:, -1]))
# 创建 kd tree
kd_left = self.create_kd_tree(data_left)
if kd_left:
kd_left.parent = kd_point
kd_point.left = kd_left
kd_right = self.create_kd_tree(data_right)
if kd_right:
kd_right.parent = kd_point
kd_point.right = kd_right
return kd_point
第五步,搜索最近邻。
def find_nearest(self, target):
if kd_tree is None:
return {
"nearest": None,
"dist": -1
}
target = np.array(target)
kd_point = kd_tree
nearest = kd_tree.data.ravel()
min_dist = np.linalg.norm(nearest - target)
search_path = []
while kd_point:
data_node = kd_point.data.ravel()
dist = np.linalg.norm(data_node - target)
split = kd_point.split
if dist < min_dist:
nearest = data_node
min_dist = dist
search_path.append(kd_point)
print(target[split])
print(data_node)
if target[split] < data_node[split]:
kd_point = kd_point.left
else:
kd_point = kd_point.right
while len(search_path) > 0:
kd_point = search_path.pop()
if kd_point is None:
continue
data_node = kd_point.data.ravel()
dist = np.linalg.norm(data_node - target)
split = kd_point.split
if dist == min_dist:
if target[split] < data_node[split]:
search_path.append(kd_point.right)
else:
search_path.append(kd_point.left)
elif dist < min_dist:
nearest = data_node
min_dist = dist
if target[split] < data_node[split]:
search_path.append(kd_point.left)
else:
search_path.append(kd_point.right)
return {
"nearest": nearest,
"dist": min_dist
}
【完整代码】:传送门
【问题】:不过上述代码仍然存在问题,尤其在数据量较小时。
- 在构造 kd-tree 之前需要对数据进行一次排序,要保证 x 和 y 之间的对应的关系,因此需要将 x 和 y 合并进行一次排序。但是,在后续操作中,两者需要分离处理,因为 x 的数值较小时,argmax() 函数可能会将 y 当作 split。
- 当数据量与 k 值比较接近时,邻域集中会出现重复的邻点,并且还需要对数据量和 k 值做判断,以应对数据量少于 k 值的情况。
- 当数据量过小时,会发生“越过根结点”的现象,即左子树(右子树)的数据量少于 k 值,此时要处理会非常麻烦。
- 仍然有个问题,越过根结点的另一子树的叶结点距 target 的值一定大于父结点的距离吗?
上述问题仍待思考…
sklearn 实现
K-近邻算法属于 sklearn.neighbors 包,具体内容可参考官网 API 传送门
【示例】:
from sklearn.neighbors import KNeighborsClassifier
X = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]
model = KNeighborsClassifier(n_neighbors=3)
model.fit(X, y)
print(model.predict([[1.1]])) # [0]
print(model.predict_proba([[0.9]])) # [[0.66666667 0.33333333]]
优缺点
【优点】:
- 算法思路较为简单,易于实现;
- 当有新样本加入到训练集中时,无需重新训练。因为 KNN 没有显式的学习过程,其所谓的学习也仅仅是将训练集保存在内存中,然后计算预测点与训练集中各点的距离;
- 计算时间和空间与训练集的规模呈线性关系,在一些场合中不算太大。
【缺点】:
- 分类速度慢:KNN 算法的时间复杂度和存储空间会随着训练集规模和特征维数的增大而快速增加。
- 各属性的权重相同,在一定程度上会影响准确率。当样本不平衡时,有可能导致新样本的 k 个邻居中大容量类的样本居多,即使距离新样本最近的几个样本都是小容量类,但最终被分到大容量类中。针对这个问题,可以考虑修改分类决策规则。
- K 值的选择需要深入考虑。
问题 QA
为什么要做数据归一化 ?
示例:使用K-近邻算法改进约会网站的配对效果 中的数据。
| 玩视频游戏所耗时间百分比 | 每年获得的飞行常客里程数 | 每周消费的冰淇淋公升数 | 样本分类 |
|---|---|---|---|
| 0.8 | 400 0.5 | 1 | |
| 12 | 134000 | 0.9 | 3 |
| 0 | 20000 | 1.1 | 2 |
| 67 | 32000 | 0.1 | 2 |
我们计算样本 1 和样本 2 之间的距离:
( 0.8 − 12 ) 2 + ( 400 − 134000 ) 2 + ( 0.5 − 0.9 ) 2 \sqrt{(0.8 - 12)^2 + (400 - 134000)^2 + (0.5 - 0.9)^2} (0.8−12)2+(400−134000)2+(0.5−0.9)2
从上述方程式中可以发现,数字差值最大的属性对计算结果的影响最大,也就是说,每年获取的飞行常客里程数对于计算结果的影响将远远大于其他两个特征属性。而产生这种现象的唯一原因,仅仅是因为飞行常客里程数远大于其他特征值。通常情况下,我们认为这三种特征是同等重要的,因此作为三个等权重的特征之一,飞行常客里程数并不应该如此严重地影响到计算结果。
基于上述原因,我们需要对数据作归一化处理。
【数据归一化】:消除数据特征之间的量纲影响,使得不同指标之间具有可比性。最常用的方法主要有以下两种。
- 线性函数归一化(Min-Max Scaling):对原始数据进行线性变换,将结果映射到 [0, 1] 范围内,实现对原始数据的等比缩放。
x n o r m = x − x m i n x m a x − x m i n x_{norm} = \frac{x - x_{min}}{x_{max} - x_{min}} xnorm=xmax−xminx−xmin - 零均值归一化(Z-Score Normalization):将原始数据映射到均值为 0、标准差为 1 的分布上。
z = x − μ σ z = \frac{x-\mu}{\sigma} z=σx−μ
以上两种方法,在 scikit-learn 的 preprocessing 包中都有实现,分别为 MinMaxScaler(feature_range=(0, 1)) 和 StandardScaler()。
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
datasets = load_iris()
x = datasets.data
mm_transformer = MinMaxScaler(feature_range=(0, 1))
new_x = mm_transformer.fit_transform(x)
print(new_x)
st_transformer = StandardScaler()
new_x = st_transformer.fit_transform(x)
print(new_x)
具体内容可参考官网 API:
- MinMaxScaler:传送门
- StandardScaler:传送门
需要注意的是,有的时候我们可能反而希望不同的特征对预测结果产生不同的影响。此时,就需要在距离公式中给特征赋予不同的权重。我们可以在对特征进行归一化处理之后,在距离公式的特征前加上权值:
0.5 × ( x i 1 − x j 1 ) 2 + 1 × ( x i 2 − x j 2 ) + ⋯ + 1.2 × ( x i m − x j m ) 2 \sqrt{0.5 \times (x_i^1 - x_j^1)^2 + 1 \times (x_i^2 - x_j^2) + \cdots + 1.2 \times (x_i^m - x_j^m)^2} 0.5×(xi1−xj1)2+1×(xi2−xj2)+⋯+1.2×(xim−xjm)2
为什么要对数据集进行降维操作?
当样本容量较大以及特征数较多时,KNN 算法分类的效率将大大降低。此时,我们需要对数据集进行降维,删除那些对分类结果影响较小的特征。
除了对数据集做降维处理,也可以考虑缩减数据集大小。当两个样本 (1.1, 3.4) 和 (1.1, 3.5) 非常接近时,可以考虑去除一个样本。上述做法也启示我们在进行 KNN 算法前先对数据集去重,可以有效缩减数据集的规模。
K 近邻法如何避免过拟合?
在先前所讲的 K 值选择 中提到,当 K 取值较小时,模型的训练误差较小而泛化误差会增加,从而导致过拟合。因此,我们可以适当增大 K 值。
如何选择 K?
可通过交叉验证和参数优化的方式选择最优的 K 值。
【示例代码】:sklearn 包
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold
from sklearn.model_selection import GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier()
param = {
'n_neighbors': [3, 4, 5, 6, 7]
}
cv = GridSearchCV(estimator=model, param_grid=param)
cv.fit(x, y)
print(cv.best_params_)
总结
参考
- 《统计学习方法》
- 《机器学习实战》
- 《百面机器学习 算法工程师带你去面试》