机器学习-线性回归-02
文章目录
-
-
- 2. 线性回归-02
-
- 2.1. 线性回归方程的实现
- 2.2. 梯度下降
-
- 2.2.1. 批量梯度下降
- 2.2.2. 随机梯度下降
- 2.2.3. MiniBatch梯度下降
- 2.2.4. 三种策略的对比
- 2.3. 多项式回归
- 2.4. 正则化
-
2. 线性回归-02
- 之前的算法模拟已经给出了求解方法,基于最小二乘法求解,但这并不是机器学习的思想,由此引入了梯度下降方法。
2.1. 线性回归方程的实现
-
先进行导包操作
import numpy as np import os %matplotlib inline import matplotlib import matplotlib.pyplot as plt # 画图展示的时候字体的大小 plt.rcParams['axes.labelsize'] = 14 plt.rcParams['xtick.labelsize'] = 12 plt.rcParams['ytick.labelsize'] = 12 # 防止版本不匹配出现警告 import warnings warnings.filterwarnings('ignore') # 指定一个随机种子,保证每次的数据都相同 np.random.seed(42) -
随机生成X和y值
rand函数是一个均匀分布的随机数函数,会返回0-1区间的随机数randn生成正态分布随机数,有正数有负数# 产生100行1列的范围是在[0-2]的随机数 X = 2 * np.random.rand(100,1) # 产生100行1列的服从均值为 0,标准差为 1 的正态分布的随机数 y = 3 * X + 4 + np.random.randn(100,1) -
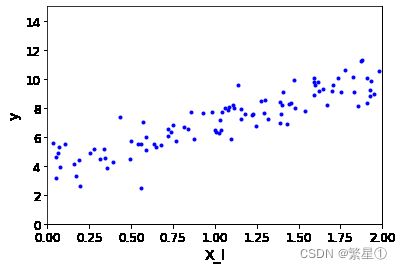
把第二步生成的点出来
plt.plot(X,y,'b.') plt.xlabel('X_l') plt.ylabel('y') plt.axis([0,2,0,15]) plt.show() -
拼接数据,方便进行数据操作
# 把常数项和原数据进行拼接 X_b = np.c_[np.ones((100,1)),X] # 具体的计算,计算曲线的斜率 theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y) theta_best -
生成曲线的参数
# 生成两行一列的数据 X_new = np.array([[0],[2]]) # 把数据与1进行拼接 X_new_b = np.c_[np.ones((2,1)),X_new] # 进行预测,生成曲线参数 y_predict = X_new_b.dot(theta_best) -
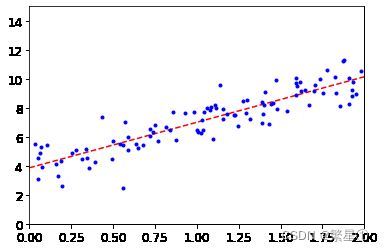
根据参数画出图形
plt.plot(X_new,y_predict,'r--') plt.plot(X,y,'b.') plt.axis([0,2,0,15]) plt.show() -
使用工具包进行训练
from sklearn.linear_model import LinearRegression lin_reg = LinearRegression() lin_reg.fit(X,y) # 获取预测的估计系数 print(lin_reg.coef_) # 获取模型中的截距项 print(lin_reg.intercept_)
2.2. 梯度下降
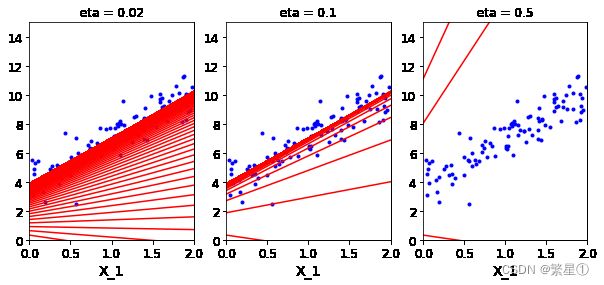
- 应当合理控制步长,如果步长过大,导致数据震荡太大,无法拟合较好的曲线;如果太小,会花费很长的时间
- 标准化的作用:拿到数据后基本上都要进行一次标准化操作
2.2.1. 批量梯度下降
- 计算公式
-
批量梯度下降
# 学习率 eta = 0.1 # 迭代次数 n_iterations = 1000 # 样本总量 m = 100 # 设置一个随机的theta值 theta = np.random.randn(2,1) # 进行迭代 for iteration in range(n_iterations): # 批量梯度下降的具体计算公式 gradients = 2/m * X_b.T.dot(X_b.dot(theta)-y) theta = theta - eta * gradients -
画图操作,注意与上面是独立的
# 画图操作 # 选择theta=0.1的学习率放入theta_path_bgd,后面用于数据的比较 theta_path_bgd = [] def plot_gradient_descent(theta,eta,theta_path = None): m = len(X_b) plt.plot(X,y,'b.') n_iterations = 1000 for iteration in range(n_iterations): y_predict = X_new_b.dot(theta) plt.plot(X_new,y_predict,'r-') gradients = 2/m * X_b.T.dot(X_b.dot(theta)-y) theta = theta - eta * gradients if theta_path is not None: theta_path_bgd.append(theta) plt.xlabel('X_1') plt.axis([0,2,0,15]) plt.title('eta = {}'.format(eta)) # 保证theta相同的条件下,改变eta的值,来判断预测函数 theta = np.random.randn(2,1) plt.figure(figsize=(10,4)) plt.subplot(131) plot_gradient_descent(theta,eta = 0.02) plt.subplot(132) plot_gradient_descent(theta,eta = 0.1,theta_path=True) plt.subplot(133) plot_gradient_descent(theta,eta = 0.5) plt.show()
2.2.2. 随机梯度下降
-
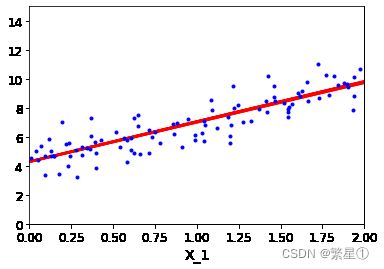
迭代的次数会越来越多
# 随机梯度下降,每次迭代1个数据 # 保存随机的theta值 theta_path_sgd = [] # 回传一个两行一列的数组 theta = np.random.randn(2,1) m = len(X_b) n_epochs = 50 # 指定衰减策略 t0 = 5 t1 = 50 # 随着迭代的进行,值会越来越小 def learning_schedule(t): return t0/(t1+t) for epoch in range(n_epochs): for i in range(m): # 为了方便显示,只迭代前几次 if epoch == 10 and i < 20: y_predict = X_new_b.dot(theta) plt.plot(X_new,y_predict,'r-') # 选择随机的一个样本 random_index = np.random.randint(m) xi = X_b[random_index:random_index+1] yi = y[random_index:random_index+1] # 计算梯度 gradients = 2 * xi.T.dot(xi.dot(theta)-yi) # 根据衰减策略进行迭代 eta = learning_schedule(epoch * m + i) theta = theta - eta * gradients theta_path_sgd.append(theta) # 展示 plt.plot(X,y,'b.') plt.xlabel('X_1') plt.axis([0,2,0,15]) plt.show()
2.2.3. MiniBatch梯度下降
-
迭代的次数一般为2的整数倍
theta_path_mgd = [] n_epochs = 50 # 每次选择16个数据进行迭代 minibatch = 16 theta = np.random.randn(2,1) t = 0 for epoch in range(n_epochs): shuffled_indices = np.random.permutation(m) X_b_shuffled = X_b[shuffled_indices] y_shuffled = y[shuffled_indices] for i in range(0,m,minibatch): # 为了方便显示,只迭代前几次 if epoch == 40 : y_predict = X_new_b.dot(theta) plt.plot(X_new,y_predict,'r-') t += 1 xi = X_b_shuffled[i:i + minibatch] yi = y_shuffled[i:i + minibatch] gradients = 2/minibatch * xi.T.dot(xi.dot(theta)-yi) eta = learning_schedule(t) theta = theta - eta * gradients theta_path_mgd.append(theta) plt.plot(X,y,'b.') plt.xlabel('X_1') plt.axis([0,2,0,15]) plt.show()
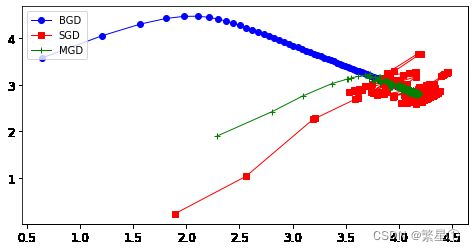
2.2.4. 三种策略的对比
- 对比实验
theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)
plt.figure(figsize=(8,4))
# 批量梯度下降
plt.plot(theta_path_bgd[:,0],theta_path_bgd[:,1],'b-o',linewidth=1,label='BGD')
# 随机梯度下降
plt.plot(theta_path_sgd[:,0],theta_path_sgd[:,1],'r-s',linewidth=1,label='SGD')
# 小批量梯度下降
plt.plot(theta_path_mgd[:,0],theta_path_mgd[:,1],'g-+',linewidth=1,label='MGD')
plt.legend(loc='upper left')
效果展示:
2.3. 多项式回归
-
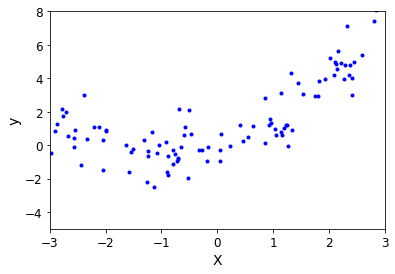
模拟数据
m = 100 X = 6 * np.random.rand(m,1) - 3 y = 0.5 * X ** 2 + X + np.random.randn(m,1) -
展示
plt.plot(X,y,'b.') plt.xlabel('X') plt.ylabel('y') plt.axis([-3,3,-5,8]) plt.show() -
多项式运算
from sklearn.preprocessing import PolynomialFeatures # 生成二次函数 poly_features = PolynomialFeatures(degree = 2,include_bias = False) # 拟合数据,然后对其进行转换,fit函数用于计算各项值,transform用于转化数据,把数据进行回传 # 回传原数据和原数据的平方项 X_poly = poly_features.fit_transform(X)获取平方项,一次项和常数项
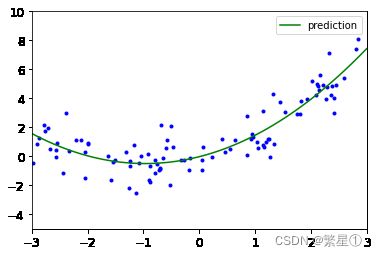
from sklearn.linear_model import LinearRegression lin_reg = LinearRegression() lin_reg.fit(X_poly,y) print(lin_reg.coef_) print(lin_reg.intercept_)画图展示
# 画图操作 X_new = np.linspace(-3,3,100).reshape(100,1) X_new_poly = poly_features.transform(X_new) y_new = lin_reg.predict(X_new_poly) plt.plot(X,y,'b.') plt.plot(X_new,y_new,'g-',label = 'prediction') plt.axis([-3,3,-5,10]) plt.legend() plt.show() -
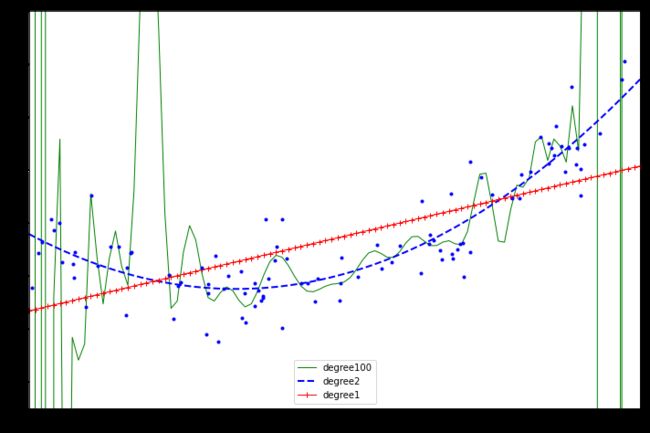
特征变换复杂度
from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler plt.figure(figsize=(12,8)) # 相应位置相互对应 for style,width,degree in (('g-',1,100),('b--',2,2),('r-+',1,1)): # 生成管道所需要的变量 poly_features = PolynomialFeatures(degree = degree,include_bias = False) std = StandardScaler() lin_reg = LinearRegression() # 管道操作 polynomial_reg = Pipeline([('poly_features',poly_features), ('StandardScaler',std), ('lin_reg',lin_reg)]) # 训练 polynomial_reg.fit(X,y) # 预测 y_new_2 = polynomial_reg.predict(X_new) # 展示 plt.plot(X_new,y_new_2,style,label = 'degree'+str(degree),linewidth = width) plt.plot(X,y,'b.') plt.axis([-3,3,-5,10]) plt.legend() plt.show()特征变换的越复杂,得到的结果过拟合风险越高,不建议做的特别复杂。
-
样本数量对结果的影响
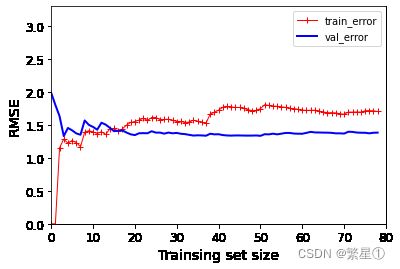
# 导入均方误差函数 from sklearn.metrics import mean_squared_error # 将数组或矩阵拆分为随机训练和测试子集 from sklearn.model_selection import train_test_split def plot_learning_curves(model,X,y): # 将数据进行拆分,测试集的比例是0.2,指定随机因子,保证每次传的值相同 X_train,X_val,y_train,y_val = train_test_split(X,y,test_size = 0.2, random_state = 0) train_errors,val_errors = [],[] for m in range(1,len(X_train)): # 选择m个数据进行训练 model.fit(X_train[:m],y_train[:m]) # 训练集的结果 y_train_predict = model.predict(X_train[:m]) # 测试集的结果 y_val_predict = model.predict(X_val) train_errors.append(mean_squared_error(y_train[:m],y_train_predict[:m])) val_errors.append(mean_squared_error(y_val,y_val_predict)) plt.plot(np.sqrt(train_errors),'r-+',linewidth = 1,label = 'train_error') plt.plot(np.sqrt(val_errors),'b-',linewidth = 2,label = 'val_error') plt.xlabel('Trainsing set size') plt.ylabel('RMSE') plt.legend()展示
lin_reg = LinearRegression() plot_learning_curves(lin_reg,X,y) plt.axis([0,80,0,3.3]) plt.show() -
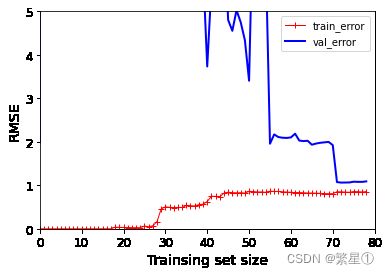
过拟合风险(越复杂越过拟合)
# 生成流水线 polynomial_reg = Pipeline([('poly_features',PolynomialFeatures(degree = 25,include_bias = False)),('lin_reg',LinearRegression())]) plot_learning_curves(polynomial_reg,X,y) plt.axis([0,80,0,5]) plt.show()
2.4. 正则化
对权重参数进行惩罚,让权重参数尽可能平滑一些,有两种不同的方法来进行正则化惩罚:
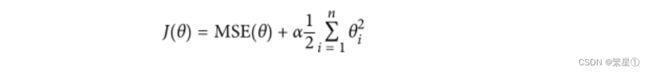
# 导入岭回归的包
from sklearn.linear_model import Ridge
# 指定随机种子
np.random.seed(42)
# 样本的数量
m = 20
# X的数据在0-3之间
X = 3 * np.random.rand(m,1)
# y的值
y = 0.5 * X + np.random.randn(m,1)/1.5 + 1
# 测试数据:指定0-3的100个数据,并且把数据转换成数组的形式
X_new = np.linspace(0,3,100).reshape(100,1)
def plot_model(model_calss,polynomial,alphas,**model_kargs):
# zip函数让alphas与括号里面的线条相对应,赋给循环变量alpha和style
for alpha,style in zip(alphas,('b-','g--','r:')):
# 线性回归模型
model = model_calss(alpha,**model_kargs)
# 二项式回归模型
if polynomial:
model = Pipeline([('poly_features',PolynomialFeatures(degree =10,include_bias = False)),('StandardScaler',StandardScaler()),
('lin_reg',model)])
# 训练
model.fit(X,y)
# 预测
y_new_regul = model.predict(X_new)
# 画图展示
lw = 2 if alpha > 0 else 1
plt.plot(X_new,y_new_regul,style,linewidth = lw,label = 'alpha = {}'.format(alpha))
plt.plot(X,y,'b.',linewidth =3)
plt.legend()
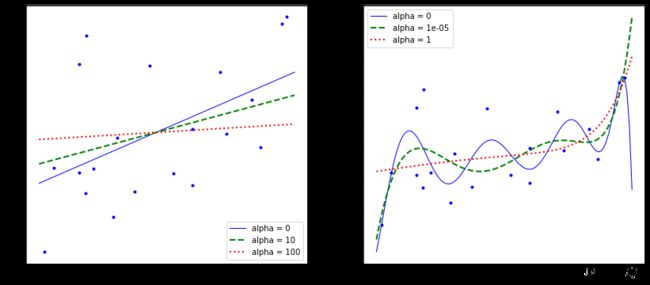
plt.figure(figsize=(14,6))
plt.subplot(121)
plot_model(Ridge,polynomial=False,alphas = (0,10,100))
plt.subplot(122)
plot_model(Ridge,polynomial=True,alphas = (0,10**-5,1))
plt.show()
效果展示:
惩罚力度越大,alpha值越大的时候,得到的决策方程越平稳。
from sklearn.linear_model import Lasso
plt.figure(figsize=(14,6))
plt.subplot(121)
plot_model(Lasso,polynomial=False,alphas = (0,0.1,1))
plt.subplot(122)
plot_model(Lasso,polynomial=True,alphas = (0,10**-1,1))
plt.show()
效果展示: