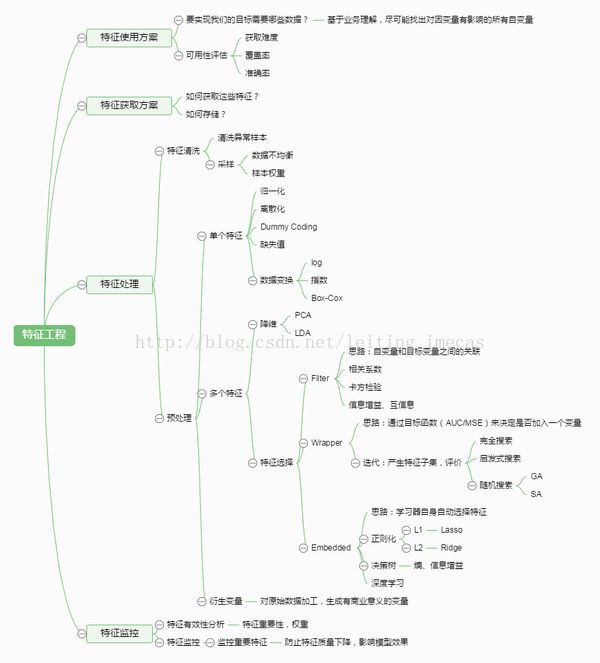
从sklearn.preprocessing, sklearn.feature_selection学习特征工程之预处理

特征工程思维导图如下图。 本文借助sklearn介绍其中的预处理部分

二 单特征预处理

       <1> 标准化   Standardization   或者叫 mean removal and variance scaling（平均值移除、方差缩放)

             说明1： 标准化其实就是干两件事：“transform the data to center” ，即使数据平均值为0；

                                                               “scale it by dividing non-constant features by their standard deviation”，即标准差为1

              (1)  sklearn 提供了scale做数据标准化：            

>>> from sklearn import preprocessing
>>> import numpy as np
>>> X = np.array([[1., -1., 2.],
...               [2.,  0., 0.],
...               [0.,  1., -1.]])
>>> X_scaled = preprocessing.scale(X)
>>> X_scaled
array([[ 0.        , -1.22474487,  1.33630621],
       [ 1.22474487,  0.        , -0.26726124],
       [-1.22474487,  1.22474487, -1.06904497]])
>>> X_scaled.mean(axis=0)
array([ 0.,  0.,  0.])
>>> X_scaled.std(axis=0)
array([ 1.,  1.,  1.])

                 preprocessing 提供了另一个实用的类StandardScaler，它的fit函数解析训练数据（包括值和矩阵格式)，transform则对

                 数据执行standardization过程。 在训练数据上使用的StandardScalar对象可以再使用在测试数据上

>>> scaler = preprocessing.StandardScaler().fit(X)
>>> scaler
StandardScaler(copy=True, with_mean=True, with_std=True)
>>> scaler.mean_
array([ 1.        ,  0.        ,  0.33333333])
>>> scaler.scale_
array([ 0.81649658,  0.81649658,  1.24721913])
>>> scaler.transform(X)
array([[ 0.        , -1.22474487,  1.33630621],
       [ 1.22474487,  0.        , -0.26726124],
       [-1.22474487,  1.22474487, -1.06904497]])
>>> X_test = np.array([[-1., 1., 0.]])
>>> scaler.transform(X_test)
array([[-2.44948974,  1.22474487, -0.26726124]])

                     StandardScaler的构造函数中可以关闭with_mean和with_std

                (2) 缩放至一定范围

                 先介绍MinMaxScaler的使用, 使用max - min作为分母

>>> X_train = np.array([[1., -1., 2.],
...                     [2., 0., 0.],
...                     [0., 1., -1]])
>>> min_max_scaler = preprocessing.MinMaxScaler()
>>> X_train_minmax = min_max_scaler.fit_transform(X_train)
>>> X_train_minmax
array([[ 0.5       ,  0.        ,  1.        ],
       [ 1.        ,  0.5       ,  0.33333333],
       [ 0.        ,  1.        ,  0.        ]])
>>> X_test = np.array([[ -3., -1.,  4.]])
>>> X_test_minmax = min_max_scaler.transform(X_test)
>>> X_test_minmax
array([[-1.5       ,  0.        ,  1.66666667]])

                   在介绍MaxAbsScaler， 将最大的绝对值作为分母

>>> max_abs_scaler = preprocessing.MaxAbsScaler()
>>> X_train_maxabs = max_abs_scaler.fit_transform(X_train)
>>> X_train_maxabs
array([[ 0.5, -1. ,  1. ],
       [ 1. ,  0. ,  0. ],
       [ 0. ,  1. , -0.5]])
>>> X_test = np.array([[ -3., -1.,  4.]])
>>> X_test_maxabs = max_abs_scaler.transform(X_test)
>>> X_test_maxabs
array([[-1.5, -1. ,  2. ]])
>>> max_abs_scaler.scale_
array([ 2.,  1.,  2.])

              如果不想创建scaler对象、不需要后面的test data上使用，可以使用 minmax_scale和maxabs_scale方法

          <2>  正则化 Normalization   (跟以前理解的正则化概念不同）

          正则化的过程是将每个样本缩放到单位范数。对于后面要通过点积或其他核方法计算两个样本之间相似性的情况，

      该正则化十分有用。

          Normalization主要思想是对每个样本计算p-范数（例如l1-范数，l2-范数等），然后样本的每个元素除以该范数。则

      执行正则化的样本的p-范数变为1。    p-范数的公式： ||X||p = (|x1|^p + |x2|^p + .... + |xn|^p)^1/p

         该方法主要用于文本分类和聚类，例如两个tf-idf向量的l2正则化进行点积就得到两个向量的余弦相似性

>>> X_normalized = preprocessing.normalize(X, norm='l2')

>>> X_normalized
array([[ 0.40824829, -0.40824829,  0.81649658],
       [ 1.        ,  0.        ,  0.        ],
       [ 0.        ,  0.70710678, -0.70710678]])

           同样提供了类：

>>> normalizer = preprocessing.Normalizer().fit(X)
>>> normalizer
Normalizer(copy=True, norm='l2')
>>> normalizer.transform(X)
array([[ 0.40824829, -0.40824829,  0.81649658],
       [ 1.        ,  0.        ,  0.        ],
       [ 0.        ,  0.70710678, -0.70710678]])
>>> normalizer.transform([[-1.,  1., 0.]])
array([[-0.70710678,  0.70710678,  0.        ]])

           

         <3> Binarization  二值化

                      特征二值化是指依据一个阈值，将大于阈值的赋值为1， 小于等于阈值的赋值为0.

>>> X
array([[ 1., -1.,  2.],
       [ 2.,  0.,  0.],
       [ 0.,  1., -1.]])
>>> binarizer = preprocessing.Binarizer().fit(X)
>>> binarizer
Binarizer(copy=True, threshold=0.0)
>>> binarizer.transform(X)
array([[ 1.,  0.,  1.],
       [ 1.,  0.,  0.],
       [ 0.,  1.,  0.]])
>>> binarizer2 = preprocessing.Binarizer(threshold=1.1)
>>> binarizer2.transform(X)
array([[ 0.,  0.,  1.],
       [ 1.,  0.,  0.],
       [ 0.,  0.,  0.]])

           <4> 类别型特征编码

           可以使用oneHot encoding 将类别型特征进行编码。

>>> enc = preprocessing.OneHotEncoder()
>>> enc.fit([[0, 0, 3], [1, 1, 0], [0, 2, 1], [1, 0, 2]])  # 第一个特征有2个类别，第二个特征有3个类别，第三个特征有4类别
OneHotEncoder(categorical_features='all', dtype=,
       handle_unknown='error', n_values='auto', sparse=True)
>>> enc.transform([[0, 0, 0]]).toarray()
array([[ 1.,  0.,  1.,  0.,  0.,  1.,  0.,  0.,  0.]])  # 第一个特征占据前两位，第二个特征占据厚3个位置，第三个特征占最后4个
>>> enc.transform([[1, 0, 0]]).toarray()
array([[ 0.,  1.,  1.,  0.,  0.,  1.,  0.,  0.,  0.]])
>>> enc.transform([[0, 1, 0]]).toarray()
array([[ 1.,  0.,  0.,  1.,  0.,  1.,  0.,  0.,  0.]])
>>> enc.transform([[0, 2, 0]]).toarray()
array([[ 1.,  0.,  0.,  0.,  1.,  1.,  0.,  0.,  0.]])
>>> enc.transform([[0, 0, 1]]).toarray()
array([[ 1.,  0.,  1.,  0.,  0.,  0.,  1.,  0.,  0.]])
>>> enc.transform([[0, 0, 2]]).toarray()
array([[ 1.,  0.,  1.,  0.,  0.,  0.,  0.,  1.,  0.]])
>>> enc.transform([[0, 0, 3]]).toarray()
array([[ 1.,  0.,  1.,  0.,  0.,  0.,  0.,  0.,  1.]])

      如果训练数据中的类别不全，则可以指定每个特征的类别数量

>>> enc = preprocessing.OneHotEncoder(n_values=[2,3,4])  #指定
>>> enc.fit([[1, 2, 3], [0, 2, 0]])
OneHotEncoder(categorical_features='all', dtype=,
       handle_unknown='error', n_values=[2, 3, 4], sparse=True)
>>> enc.transform([[1, 2, 0]]).toarray()
array([[ 0.,  1.,  0.,  0.,  1.,  1.,  0.,  0.,  0.]])
>>> enc.transform([[1, 0, 0]]).toarray()
array([[ 0.,  1.,  1.,  0.,  0.,  1.,  0.,  0.,  0.]])
>>> enc.transform([[1, 1, 0]]).toarray()
array([[ 0.,  1.,  0.,  1.,  0.,  1.,  0.,  0.,  0.]])

             <5> 缺省值计算 ---------Imputer

    

>>> from sklearn.preprocessing import Imputer
>>> imp = Imputer(missing_values='NaN', strategy='mean', axis=0)
>>> imp
Imputer(add_indicator_features=False, axis=0, copy=True, missing_values='NaN',
    strategy='mean', verbose=0)
>>> imp.fit([[1, 2], [np.nan, 3], [7, 6]])   #第一维的平均值为4， 第二维的平均值为3.667
Imputer(add_indicator_features=False, axis=0, copy=True, missing_values='NaN',
    strategy='mean', verbose=0)
>>> X = [[np.nan, 2], [6, np.nan], [7, 6]]
>>> imp.transform(X)
array([[ 4.        ,  2.        ],
       [ 6.        ,  3.66666667],
       [ 7.        ,  6.        ]])

           <6> 特征的多项式变换

                多项式变换会将每个样本数据扩展为原本元素的多项式项，例如

                （X1， X2) 经过二项式变换，变为(1, X1, X2, X1^2, X1X2, X2^2)

>>> X = np.arange(6).reshape(3,2)
>>> X
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly = preprocessing.PolynomialFeatures(2) #指定二项式变化
>>> poly.fit_transform(X)
array([[  1.,   0.,   1.,   0.,   0.,   1.],
       [  1.,   2.,   3.,   4.,   6.,   9.],
       [  1.,   4.,   5.,  16.,  20.,  25.]])

               还可以指定只保留互动项：

                （X1， X2) 经过二项式变换只保留互动项，变为(1, X1, X2,  X1X2)

>>> X
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly2 = preprocessing.PolynomialFeatures(degree=2, interaction_only=True)
>>> poly2.fit_transform(X)
array([[  1.,   0.,   1.,   0.],
       [  1.,   2.,   3.,   6.],
       [  1.,   4.,   5.,  20.]])

           <7> 自定义变换

            可是使用FunctionTransformer指定一个子选择的变换方法

>>> from numpy import log1p  # log1p(x) = log(1 + x)
>>> from sklearn.preprocessing import FunctionTransformer
>>> trans = FunctionTransformer(log1p)
>>> X = np.array([[0,1], [2, 3]])
>>> trans.transform(X)
array([[ 0.        ,  0.69314718],
       [ 1.09861229,  1.38629436]])

三 特征选择

     <1> Filter 过滤法   ---------多使用于线性的模型

             1.1 方差选择法

                   删除元素方差小于等于阈值的特征

                   例如，假设data中每个特征是二项分布（n次伯努利分布），而伯努利分布的方差(variance）Var = p(1-p)

               

>>> from sklearn.feature_selection import VarianceThreshold
>>> X = [[0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 1, 1], [0, 1, 0], [0, 1, 1]]
>>> sel = VarianceThreshold(threshold=(.8 * (1 - .8)))   #
>>> sel.fit_transform(X)
array([[0, 1],
       [1, 0],
       [0, 0],
       [1, 1],
       [1, 0],
       [1, 1]])

              1.2 Univariate feature selection------ 单变量特征选择

                  1.2.1 SelectKBest  ------保留k个最好的特征。   打分方法，例如卡方验证

                   1.2.2 SelectPercentile------- 保留一定比例            

>>> from sklearn.datasets import load_iris
>>> from sklearn.feature_selection import SelectKBest
>>> from sklearn.feature_selection import chi2
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> X.shape
(150, 4)
>>> X_new = SelectKBest(chi2, k=2).fit_transform(X, y)
>>> X_new.shape
(150, 2)

     <2> Wrapper --- 包裹法

           把特征选择看做一个特征子集搜索问题，筛选各种特征子集，用模型评估效果。

           介绍RFE--- recursive feature elemination, 递归消除特征法， 每轮训练，消除权值小的一定比例的特征，在基于新特征训练，如果满足

               期望要求，继续消除，以此递归，直到模型效果低于预期值。以LR为例，过程如下：

               1. 使用全特征跑一个模型

               2.根据线性模型的系数（体现相关性），删掉5%-10%的弱特征，观察准确率/auc变化

               3. 逐步进行，知道准确率/auc出现大的下滑停止

             class sklearn.feature_selection.RFE(estimator, n_features_to_select=None, step=1, verbose=0)

           n_featuers_to_select ------保留的特征个数， 不指定则保留一半

           step-----每次要消除的特征。 如果>1, 表示每次删除的个数； 如果[0,1]之间，表示每次删除的比例

>>> from sklearn.feature_selection import RFE
>>> from sklearn.linear_model import LogisticRegression
>>> rfe = RFE(LogisticRegression(), n_features_to_select=1, step=1)
>>> rfe.fit(X, y)

    <3> Embedded -----嵌入法,  SelectFromModel

         class sklearn.feature_selection.SelectFromModel(estimator, threshold=None, prefit=False)

             estimator ----- 用来选择特征的模型

             threshold ----- 阈值。  保留大于阈值的特征。如果没有指定，且estimator有penalty=l1或者

                                     estimator为Lasso, 默认阈值为1e-1, 否则默认值为平均值

              prefit  --------是否需要先fit的模型

         (1) 基于L1正则化的特征选择方法

        先了解L1正则化：http://blog.csdn.net/leiting_imecas/article/details/56351806

         L1正则化可以用在维数很大时做特征选择.

         SelectFromModel其实就是先用一个模型（通常选择线性模型）跑一下，把特征选择出来

>>> from sklearn.svm import LinearSVC
>>> from sklearn.datasets import load_iris
>>> from sklearn.feature_selection import SelectFromModel
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> X.shape
(150, 4)
>>> lsvc = LinearSVC(C=0.01, penalty="l1", dual=False).fit(X,y)
>>> model = SelectFromModel(lsvc, prefit=True)
>>> X_new = model.transform(X)
>>> X_new.shape
(150, 3)

         sklearn说明文档上说，选择特征的模型的选择问题：

         linear_model.Lasso --------用于regression; 

         linear_model.LogisticRegression 和svm.LinearSVC ----------用于classification

        （2）基于树的特征选择

           基于树的模型可以用来计算特征的重要性，这样也可以用来去除关联性小的特征

            

>>> from sklearn.ensemble import ExtraTreesClassifier
>>> from sklearn.datasets import load_iris
>>> from sklearn.feature_selection import SelectFromModel
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> X.shape
(150, 4)
>>> clf = ExtraTreesClassifier()
>>> clf = clf.fit(X,y)
>>> clf.feature_importances_
array([ 0.05517225,  0.06978394,  0.52250383,  0.35253998])  #特征重要性
>>> model = SelectFromModel(clf, prefit=True)
>>> X_new = model.transform(X)
>>> X_new.shape
(150, 2)

[source]