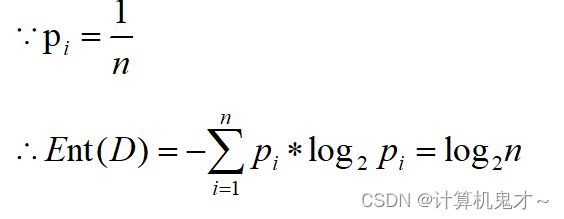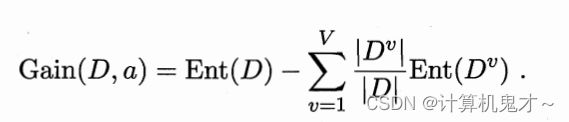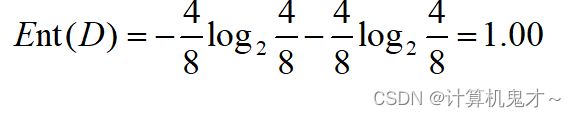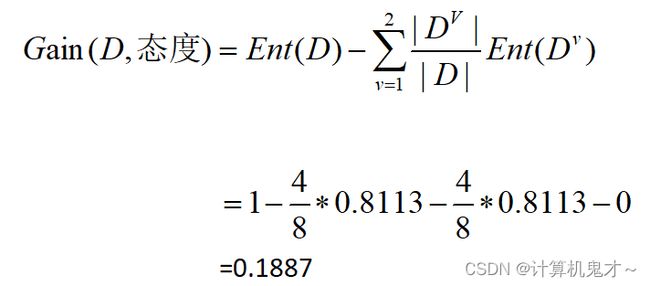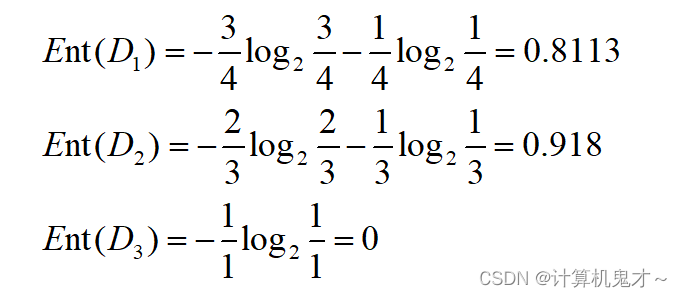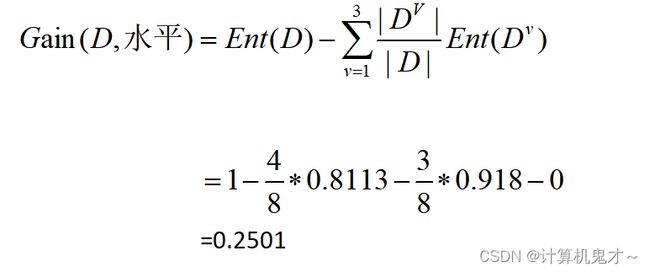决策树（1）

目录

一、引例以及“树”模型的相关介绍

1、引例

2、相关概念

二、决策树构建法之ID3算法

        1、信息熵

2、信息增益

3、ID3算法

---

一、引例以及“树”模型的相关介绍

1、引例

在正式将决策树之前，小编决定将一个大家耳熟能详的例子

引例：有一个人骑着摩托车前来买瓜，此人姓刘名华强。

他对老板说：“哥们儿，你这瓜多少钱一斤呐？”

瓜老板回答：“两块钱一斤”

华强呵呵一笑，回应老板说：“你这瓜皮子是金子做的还是瓜粒子是金子做的？”

“你瞧瞧现在哪有瓜啊？”老板不屑一顾的回答道，“这都是大棚的瓜，你嫌贵我还嫌贵呢 ”

“你给我挑一个。”华强说。

老板拍了拍瓜，拍瓜的声音浊响。问华强：“这瓜怎么样”。

华强一脸严肃的问老板：“这瓜保熟吗？”

老板回应道：“我开水果摊的，能卖给你生瓜蛋子？”

……

华强最后回应了一句：“你这瓜要是保熟，我肯定买呀”

……

想必，此例子大家多多少少都在某音或者某站看到过，小编在这里就不写后续的故事啦，感兴趣的小伙伴可以待会去看一看。

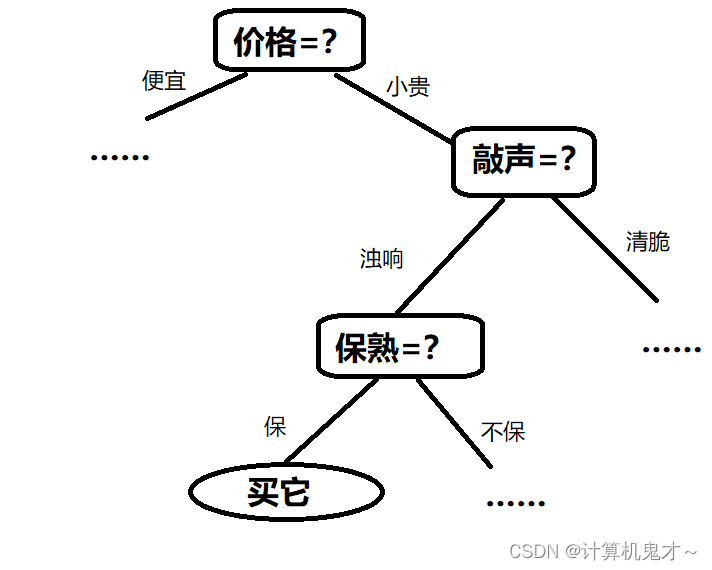
我们用树状图来描绘一下华强买瓜的心路历程：

 这张图就是我们今天的主角————决策树！

2、相关概念

        不过想要学好决策树，我们得先学好树状图的概念及与其相关的学术概念。有点小小的复杂，不过为了学知识，请大家耐心看完。

        树状图是一种数据结构，它是由n(n>=1)个有限节点组成一个具有层次关系的集合。叫做"树"是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点:①每个节点有零个或多个子节点;②没有父节点的节点称为根节点;③每一个非根节点有且只有一个父节点;④除了根节点外，每个子节点可以分为多个不相交的子树。

节点的度:一个节点含有的子树的个数称为该节点的度;

叶节点或终端节点:度为0的节点称为叶节点;

双亲节点或父节点:若一个节点含有子节点，则这个节点称为其子节点的父节点;

孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;

兄弟节点:具有相同父节点的节点互称为兄弟节点;

树的度:一棵树中，最大的节点的度称为树的度;

节点的层次:从根开始定义起，根为第1层，根的子节点为第2层，以此类推;

树的高度或深度:树中节点的最大层次;

子孙:以某节点为根的子树中任一节点都称为该节点的子孙。

森林:由m(m>=0)棵互不相交的树的集合称为森林;

好，学完了上述概念，请根据华强买瓜的那个图回答：“买它”是______节点，“价格=?”节点的度为_____,“买它”是“保熟=？”的______节点。

答案依次为：叶/终端；2；子/孩子

怎么样？聪明的读者是否做对了呢？

二、决策树构建法之ID3算法

        从上面的学习以及“决策树”这个名字，我们大致能猜得出，决策树是帮助我们判断的一种工具。那么如何选择根节点（比如说买瓜的时候先看价格还是先看是否保熟）、如何构建它的分支节点等问题的回答就显得至关重要了。

        为了解决上述问题，接下来介绍两个帮助我们用ID3算法构建决策树的重要概念——信息熵与信息增益

1、信息熵

        相信很多读者在高中化学课上学过“熵”的含义，它代表着一种事物的复杂度。熵增意味着复杂度与混乱度的提升，熵减代表着复杂度与混乱度的减小。信息熵也是一种熵，它是我们用以描述信息源的不确定度。信息熵越大，可能性越大。并且我们可以发现信息量越小，不确定性越小，熵越小。信息熵的数学公式为：

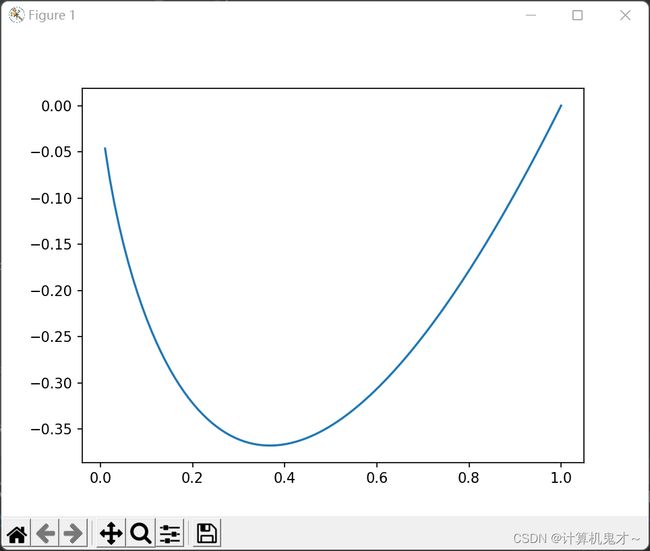
 pk代表着在D样本集合中，第k类所占的比例是多少。显然pk是一个大于0小于等于1的数，那么，取对数之后，就会变成一个负数，这就是为什么在这个公式前面会加上一个负号的原因。对于函数f(X)=x*log2x而言，其对应的函数图像为：

 也就是说，当只有一类的时候，信息熵为0，此时混乱度越小，刚好与我们的理论相对应。（比如说你去买菜，菜场里只有辣椒了，为了有吃的，那么你只能买辣椒，其不确定性为0，这是个极端的例子）；而假设有很多类（n类）时，假设每类出现的可能性相同，那么信息熵为：

 这说明了类的增多可能会造成信息熵的增大。

2、信息增益

        既然我们想要通过决策树分类，那么，我们是希望每分类一次，得到结果的熵值变得越小越好，对吧？（理解不了就想想熵的意义，熵代表着不确定性，而我们希望我们越分结果越确定，并且不确定性越小越好。）

        那么这时，我们就需要引入信息增益这个概念了，它是用某个分类条件分类作为树的节点后，信息熵减少了多少的衡量标准。我们更愿意选择信息增益大的条件，作为下次分类使用的节点。信息增益的公式如下图：

 v表示用此条件后，会被分成的类别数。比如说华强买瓜中，用“保熟”作为标准，那么就会有保熟和不保熟两类，v=2。|Dv|/|D|代表着权重，即分到第v类的样本，占总样本个数的比例。

3、ID3算法

        让信息增益越大越好构建决策树的算法，我们称之为ID3算法。接下来，小编将举一个例子，希望能帮助大家理解ID3算法构建树的过程。

例题：已知吴江中学要从自己的实习生中，选出录取的实习生，请根据下列数据，利用ID3算法，构建出一棵决策树。

 并且通过决策树判断，学校是否要录取研究生毕业，很勤快但是教学水平中等的李老师

好，审完题目后，我们决定要构建决策树啦，首先，要确定根节点。显然有以下三种情况①学历作为根节点②教学态度作为根节点③教学水平作为根节点。那么我们逐个计算信息增益时都要算没有分类时的信息熵：

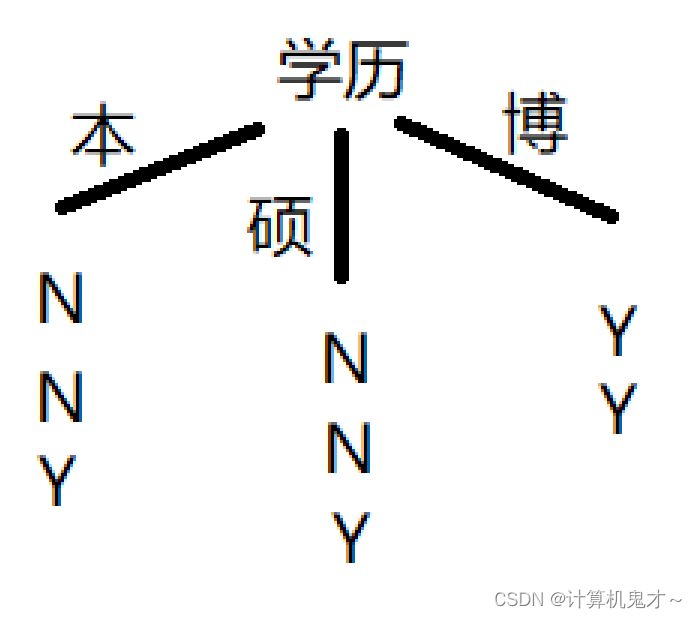
 ①学历：先画一个简单的图方便我们计算（N代表不录取，Y代表录取）

 对于本、硕、博三个子集，用“学历”划分后3个分支的信息熵为：

 根据上述三式子，可以计算出属性“学历”的信息增益为

 ②教学态度

 同理，对于懒与勤奋这两个节点，信息熵为：

 教学态度的信息增益为：

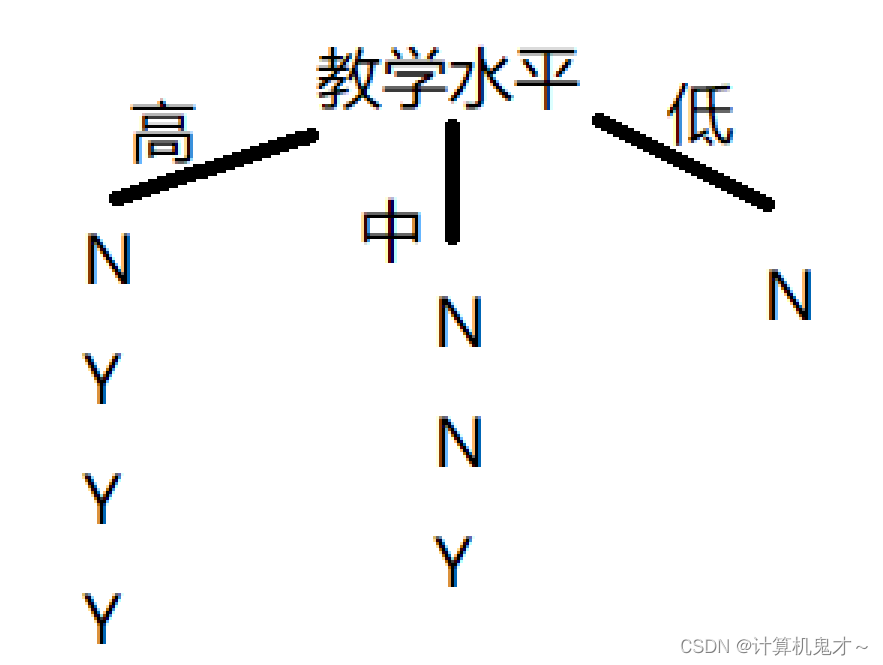
 ③教学水平

 用教学水平划分后，三个节点信息熵分别为

 信息增益为：

 

 所以，“学历”的信息增益最大，也就是说，“学历”会被当成根节点

那么接下来就很好判断了，甚至不用计算，通过观察都能得出，在“本科”这一数据集中，“教学态度”比“教学水平”更适合当节点，因为懒的都没被录取，而勤奋的都被录取了。而在“研究生”数据集中，“教学水平”则更适合当节点，因为用“教学态度”的话还要再分一次，而“教学水平”高中低刚好各一个，信息熵均为0。

所以，我们可以作图如下：

 显然，学校根据ID3算法不会录取李老师

        好的，本期的文章到这里就结束啦，想要学习C4.5决策树算法以及剪枝的相关知识，请关注小编，小编将在下期讲解此内容。

        客官，真的不给小编点个赞再走吗？小编在此谢谢啦！