激光IMU融合——LIO-Mapping / LIOM / LINS / LIO-SAM算法解析

激光IMU融合——LIO-Mapping / LIOM / LINS / LIO-SAM算法解析

在激光SLAM领域，LOAM、Lego-LOAM属于纯激光领域，除此之外还衍生处理视觉激光结合、激光IMU结合，甚至三者结合的算法，视觉激光结合的算法在我之前写的博文视觉激光融合——VLOAM / LIMO算法解析中有简单总结，本文所介绍的LIO-Mapping / LIOM / LINS / LIO-SAM算法就隶属于激光IMU结合的算法，在发展成熟度上面是要优于视觉激光融合的。

因为我是先学习的视觉SLAM算法，从整体框架上理解，LIOM、LINS类似于MSCKF，后端是基于滤波的方法实现两种传感器的紧耦合，而LIO-Mapping类似于VINS-Mono，后端是基于优化的方法实现两种传感器的紧耦合，LIO-SAM后端是基于因子图实现的多种传感器的紧耦合，对MSCKF和VINS-Mono不了解的同学可以如下参考博客：
VINS-Mono关键知识点总结——前端详解
VINS-Mono关键知识点总结——边缘化marginalization理论和代码详解
VINS-Mono关键知识点总结——预积分和后端优化IMU部分

学习MSCKF笔记——前端、图像金字塔光流、Two Point Ransac
学习MSCKF笔记——四元数基础
学习MSCKF笔记——真实状态、标称状态、误差状态
学习MSCKF笔记——后端、状态预测、状态扩增、状态更新
本篇博客，我对以上算法进行简单总结。

1. LIO-Mapping

LIO-Mapping是2019年发表于ICRA一篇论文，原论文为《Tightly Coupled 3D Lidar Inertial Odometry and Mapping》，从工程层面上将，就是LOAM和VINS-Mono的结合，具体介绍如下：

1.1 总体框架

LIO-Mapping总体框架如下：

具体步骤如下：

1. 在激光雷达数据$S_j$到来之前，IMU原始输入${\mathcal{I}}_{i,j}$进行积分（State prediction）和预积分（Pre-intergration），积分的目的是为了获得我们需要估计的状态变量${\mathbf{p}}_{B_i}^W$，${\mathbf{v}}_{B_i}^W$和${\mathbf{q}}_{B_i}^W$，而预积分的目的是为了获得用于联合优化的$\Delta {\mathbf{p}}_{ij}$，$\Delta {\mathbf{v}}_{ij}$和$\Delta {\mathbf{q}}_{ij}$；
2. 当系统收到借光雷达数据$S_j$后，对激光雷达进行去畸变操作（De-skewing）获得去畸变点云$S_j$，然后在此基础上对去畸变点云提取激光雷达特征点${\mathbf{F}}_{L_j}$（Feature extraction）；
3. 在滑动窗口内的激光雷达特征${\mathbf{F}}_{L_{o,i}}$根据优化后的位姿${\mathbf{T}}_{B_{o,i}}^W$和${\mathbf{T}}_B^L$组成局部地图${\mathbf{M}}_{L_{o,i}}^{L_p}$（Local map management），根据预测的位姿实现当前帧激光特征点和局部地图的匹配（FInd relative lidar measurements）；
4. 最后就是j激光雷达观测${\mathbf{m}}_{L_{p+1,j}}$以及预积分结果$\Delta {\mathbf{p}}_{ij}$，$\Delta {\mathbf{v}}_{ij}$和$\Delta {\mathbf{q}}_{ij}$实现联合优化，优化后的结果用于跟新IMU积分获得的状态变量，避免IMU漂移；

由于激光雷达去畸变及特征提取、预积分、边缘化等操作在VINS-Mono的相关博客中都有详细介绍，因此本篇博客只对LIO-Mapping中较为特殊的滑窗管理和地图注册进行总结

1.2 滑窗管理

LIO-Mapping中滑窗管理示意图如下：

其中，
$o$是滑窗中的第一帧Lidar Sweep，
$i$是滑窗中最后一帧Lidar Sweep，
$j$是当前帧的Lidar Sweep，
$p$是滑窗中的Pivot Lidar Sweep，所谓Pivot Lidar Sweep指的就是整个滑窗内帧的位姿都是基于该帧坐标系建立的，随着滑窗移动，Pivot Lidar Sweep也不断变化。

我们将滑窗内的特征点构建为局部地图${\mathbf{M}}_{L_o,i}^{L_p}={\mathbf{F}}_{L_{\gamma }}^{L_p},\gamma \in \{o,\dots ,i\}$，然后我们通过KNN算法找到原始特征点${\mathbf{F}}_{L_{\alpha }},\alpha \in \{p+1,\dots ,j\}$与局部地图的对应关系并构建点到面的残差，优化过程中会优化窗口中所有帧相对Pivot Lidar Sweep的相对位姿以${\mathbf{T}}_{L_p}^W$及包括Pivot Lidar Sweep的位姿${\mathbf{T}}_{L_p}^W$，而其中相对位姿可以表示为：$${\mathbf{T}}_{L_{\alpha }}^{L_p}={\mathbf{T}}_B^L{\mathbf{T}}_{B_p}^W{}^{-1}{\mathbf{T}}_{B_{\alpha }}^W{\mathbf{T}}_B^{L-1}=\left[\begin{array}{cc}{\mathbf{R}}_{L_{\alpha }}^{L_p}& {\mathbf{p}}_{L_{\alpha }}^{L_p}\\ 0& 1\end{array}\right]$$那么激光雷达的点到面的残差可以表示为：$${\mathbf{r}}_{\mathcal{L}}\left(m,{\mathbf{T}}_{L_p}^W,{\mathbf{T}}_{L_{\alpha }}^W,{\mathbf{T}}_B^L\right)={\mathbf{\omega }}^T\left({\mathbf{R}}_{L_{\alpha }}^{L_p}x+{\mathbf{p}}_{L_{\alpha }}^{L_p}\right)+d$$结合边缘化残差和预积分残差，整个优化的代码函数为$$\begin{array}{c}{\min }_{\mathbf{X}}\frac{1}{2}\{{\Vert {\mathbf{r}}_{\mathcal{P}}(\mathbf{X})\Vert }^2+{\sum }_{\genfrac{}{}{0ex}{}{m\in {\mathbf{m}}_{L_{\alpha }}}{\alpha \in \{p+1,\cdots ,j\}}}{\Vert {\mathbf{r}}_{\mathcal{L}}(m,\mathbf{X})\Vert }_{{\mathbf{C}}_{L_{\alpha }}^m}^2\\ +{\sum }_{\beta \in \{p,\cdots ,j-1\}}{\Vert {\mathbf{r}}_{\mathcal{B}}\left(z_{\beta +1}^{\beta },\mathbf{X}\right)\Vert }_{{\mathbf{C}}_{B_{\beta +1}}^{B_{\beta }}}^2\}\end{array}$$其中${\mathbf{r}}_{\mathcal{P}}(\mathbf{X})$是边缘化残差，${\mathbf{r}}_{\mathcal{L}}(m,\mathbf{X})$为激光雷达残差，${\mathbf{r}}_{\mathcal{B}}\left(z_{\beta +1}^{\beta },\mathbf{X}\right)$为预积分残差，优化变量为$$\mathbf{X}=\left[{\mathbf{X}}_{B_p}^W,\dots ,{\mathbf{X}}_{B_j}^W,{\mathbf{T}}_B^L\right]$$其中$${\mathbf{X}}_{B_i}^W=[{\mathbf{p}}_{B_i}^{W^T}{\mathbf{v}}_{B_i}^{W^T}{\mathbf{q}}_{B_i}^{W^T}{\mathbf{b}}_{a_i}^T{\mathbf{b}}_{g_i}{}^T{]}^T$$$${\mathbf{T}}_B^L={\left[\begin{array}{ll}{\mathbf{p}}_B^{L^T}& {\mathbf{q}}_B^{L^T}\end{array}\right]}^T$$

1.3 地图注册

在优化获得位姿后，论文还有一步Refinement with Rotational Constraints的过程，就是将当前帧的激光雷达点注册到全局地图中去，这也是为什么叫LIO-mapping的原因，大致流程如下：$${\mathbf{C}}_{\mathcal{M}}=\sum _{m\in {\mathbf{m}}_L}{\Vert {\mathbf{r}}_{\mathcal{M}}\left(m,{\mathbf{T}}_L^W\right)\Vert }^2，{\mathbf{r}}_{\mathcal{M}}(m,\mathbf{T})={\mathbf{\omega }}^T(\mathbf{R}\mathbf{x}+\mathbf{p})+d$$其中，${\mathbf{T}}_L^W$为前一步估计出来的位姿，${\mathbf{J}}_{\mathrm{p}}^{\mathrm{C}}$和${\mathbf{J}}_{\mathrm{p}}^{\mathrm{C}}$为残差相对位置和姿态的雅克比，为了保证地图和重力是对齐的，因此采用$SE(2)-Constraint$优化，由于Yaw方向姿态有更高的不确定性，而Roll和Pitch相对更加准确，因此对姿态的雅克比进行了限制$${\mathbf{J}}_{{\mathbf{\theta }}_z}^{\mathbf{C}}={\mathbf{J}}_{\mathbf{\theta }}^{\mathbf{C}}\cdot (\breve{\mathbf{R}}{)}^T\cdot {\breve{\mathbf{\Omega }}}_z$$$$c{\breve{\Omega }}_z=\left[\begin{array}{ccc}{ϵ}_x& 0& 0\\ 0& {ϵ}_y& 0\\ 0& 0& 1\end{array}\right]$$其中，$(\breve{\mathbf{R}})$为上一次迭代的状态，${\breve{\Omega }}_z$是姿态相对与世界坐标系的信息矩阵的近似值，${ϵ}_x,{ϵ}_y$通过Information Ratio获得。在优化步骤中通过${ϵ}_x,{ϵ}_y$计算增量$\delta {\theta }_z$和$\delta \mathbf{p}$，然后再进行状态更新$$\tilde{\mathbf{p}}=\breve{\mathbf{p}}+\delta \mathbf{p}$$$$\tilde{\mathbf{q}}=\left[\begin{array}{c}\frac{1}{2}\delta {\mathbf{\theta }}_z\\ 1\end{array}\right]\otimes \breve{\mathbf{q}}$$

1.4 实验结果

上表是消融实验的结果，LIO-raw指的是不对激光雷达进行运动补偿的结果，LIO-no-ex值得是没有进行在线外参估计的方法，LIO是带有滑窗优化的方法，LIO-mapping是带有Rotation Constraints的方法，从结果看，LIO-mapping效果确实更好。该算法效果有所提升，但是由于计算量较大没法到达实时运行。

2. LIOM

LIOM是2019年发表于IROS的一篇文章，该文章原标题为《A Robust Laser-Inertial Odometry and Mapping Method for Large-Scale Highway Environments》，标题中的For Highway Environments主要体现在利用IMU对输入进行去畸变操作，以及使用NN对点云进行语义分割，去除运动物体的影响，具体如下：

2.1 总体框架

LIOM算法总体框架如下：

如上图所示，算法由四个模块组成，其中Scan Pre-process负责进行激光点云去畸变操作；Dynamic Object Detection负责通过语义分割进行动态物体检测；Laser-Inertial Odometry就是其中最核心的部分，实现激光IMU紧耦合；Laser Mapping负责利用Odometry的输出建立全局地图，然后使用当前帧激光点云和全局地图进行NDT来实现定位结果的Refinement。这里，我们简单回顾下基于误差状态扩展卡尔曼滤波的紧耦合操作。

2.2 误差状态扩展卡尔曼滤波

原论文中这一部分的推导其实让我有点懵，我结合我自己的理解，对论文中的公式进行了一些修改，如果有问题欢迎大家指出。首先，在误差状态扩展卡尔曼滤波中要区分真实状态$x$，标称状态$\hat{x}$和误差状态$\mathbf{\delta }x$的区别，他们的关系如下：$$x=\hat{x}\oplus \mathbf{\delta }x$$LIOM中没有对外参进行在线估计（MSCKF中有），因此误差状态变量相对简单，如下：$$\delta x=\left[\begin{array}{c}\delta v\\ \delta p\\ \delta \theta \\ \delta a_b\\ \delta w_b\end{array}\right]$$误差状态变量的运动学方程如下：$$\delta \dot{x}=\left[\begin{array}{c}\delta \dot{v}\\ \delta \dot{p}\\ \delta \dot{\theta }\\ \delta {\dot{a}}_b\\ \delta {\dot{w}}_b\end{array}\right]=\left[\begin{array}{c}-\hat{R}{\left[a_m-{\hat{a}}_b\right]}_{\times }\delta \theta -\hat{R}\delta a_b-\hat{R}{a}_n\\ \delta v\\ -{\left[w_m-{\hat{w}}_b\right]}_{\times }\delta \theta -\delta w_b-w_n\\ a_w\\ w_w\end{array}\right]$$根据运动学方程就可以获得方差传递方程：$${\bar{\Sigma }}_{t+1}=F_x{\Sigma }_t{F}_x^T+F_n{Q}_n{F}_n^T$$
而对于标称状态变量直接根据欧拉积分就可以推导获得$$\left[\begin{array}{c}{\hat{v}}_{t+1}\\ {\hat{p}}_{t+1}\\ {\hat{R}}_{t+1}\\ {\hat{a}}_{b(t+1)}\\ {\hat{w}}_{b(t+1)}\end{array}\right]=\left[\begin{array}{c}{\hat{v}}_t+\left[{\hat{R}}_t\left(a_m-{\hat{a}}_{b(t)}\right)+g\right]\Delta t\\ {\hat{p}}_t+{\hat{v}}_t\Delta t+\frac{1}{2}\left[{\hat{R}}_t\left(a_m-{\hat{a}}_{b(t)}\right)+g\right]\Delta t^2\\ {\hat{R}}_{t}R\left\{\left(w_m-{\hat{w}}_{b(t)}\right)\Delta t\right\}\\ {\hat{a}}_{b(t)}\\ {\hat{w}}_{b(t)}\end{array}\right]$$以上基本上就是扩展卡尔曼滤波的预测过程，以下则是更新过程：
观测模型如下：$$\delta y=H\delta x=\left[\begin{array}{ccccc}0& I_3& 0& 0& 0\\ 0& 0& I_3& 0& 0\end{array}\right]\delta x$$通过预测过程，我们可以获得一个先验的状态变量及方差$\delta {\bar{x}}_{t+1}^m\in {\mathbb{R}}^6,{\bar{\Sigma }}_{t+1}^m\in {\mathbb{R}}^{6\times 6}$，根据先验的状态变量及方差，基于NDT算法，我们可以获得后验状态变量及方差$\delta x_{t+1}^m\in {\mathbb{R}}^6$ , ${\Sigma }_{t+1}^m\in {\mathbb{R}}^{6\times 6}$，根据先验和后验的误差，我们就可以计算出观测以及观测误差的大小：$$C_{t+1}^m={\left({\Sigma }_{t+1}^m-{\left({\bar{\Sigma }}_{t+1}^m\right)}^{-1}\right)}^{-1}$$$$\delta y_{t+1}^m={\left(K^m\right)}^{-1}\left(\delta x_{t+1}^m-\delta {\bar{x}}_{t+1}^m\right)+\delta {\bar{x}}_{t+1}^m$$其中，$K^m={\bar{\Sigma }}_{t+1}{H}^{mT}{\left(H^m{\bar{\Sigma }}_{t+1}{H}^{mT}+C_{t+1}^m\right)}^{-1}\in {\mathbb{R}}^{6\times 6}$这一步成为inversing the kalman filter measurement update，有了观测之后，我们就可以进行正常的卡尔曼更新了，如下：$$K={\bar{\Sigma }}_{t+1}{H}^T\left(H{\bar{\Sigma }}_{t+1}{H}^T+C_{t+1}\right)$$$$\delta x_{t+1}=K\left(\delta y_{t+1}-H\delta {\bar{x}}_{t+1}\right)$$$${\Sigma }_{t+1}=\left(I_{15}-KH\right){\bar{\Sigma }}_{t+1}$$最后进行误差矫正即可，如下：$$\left[\begin{array}{c}{\hat{v}}_{t+1}\\ {\hat{p}}_{t+1}\\ {\hat{R}}_{t+1}\\ {\hat{a}}_{b(t+1)}\\ {\hat{w}}_{b(t+1)}\end{array}\right]=\left[\begin{array}{c}{\hat{v}}_t+\delta v_{t+1}\\ {\hat{p}}_t+\delta p_{t+1}\\ {\hat{R}}_t\cdot R\left(\delta {\theta }_{t+1}\right)\\ {\hat{a}}_{bt}+\delta a_{b(t+1)}\\ {\hat{w}}_{bt}+\delta w_{b(t+1)}\end{array}\right]$$
以上就可以输出100HZ的激光IMU融合结果

2.2 实验结果

在论文中，作者在高速公路数据集上对比了LIOM，LOAM和SuMa三种算法的结果，如下所示：

在高速公路数据集上，LIOM确实有突出表现，建图效果对比如下所示：

3 . LINS

LINS是2020年发表于ICRA上的一篇文章，原论文名称为《LINS: A Lidar-Inertial State Estimator for Robust and Efficient
Navigation》，该论文的主要特点在于使用了基于误差状态的迭代扩展卡尔曼滤波，并且以机器人中心重新定义了状态变量，论文还和LIO-Mapping进行了对比，在精度相同的情况下取得了更高的效率。

3.1 总体框架

算法总体框架如下：

算法整体框架也是非常清晰明了，Feature Extraction Module主要用于提取激光雷达特征点，Lidar-inertial Odometry Module就是通过卡尔曼滤波融合激光雷达特征点和IMU，Mapping Module主要利用全局地图来Refine里程计的结果。由于Feature Extraction Module主要参考的LOAM和Lego-LOAM算法，这里我们主要总结其中核心的卡尔曼滤波融合部分。

3.2 误差状态扩展卡尔曼滤波

LINS中的误差状态扩展卡尔曼滤波的特点主要是：

1. 以机器人中心定义的状态变量，避免了在线性化过程中不断增大的不确定性；
2. 使用迭代扩展卡尔曼滤波，以取得更高的精度；

下面具体展开，在LIOM算法中，所有状态变量都是建立在世界坐标系下，并对其进行拓展卡尔曼滤波，这样由于线性化导致的误差是在不断累积的，但是在LINS，状态变量定义如下：$${\mathbf{x}}_w^{b_k}:=\left[{\mathbf{p}}_w^{b_k},{\mathbf{q}}_w^{b_k}\right]$$$${\mathbf{x}}_{b_{k+1}}^{b_k}:=\left[{\mathbf{p}}_{b_{k+1}}^{b_k},{\mathbf{v}}_{b_{k+1}}^{b_k},{\mathbf{q}}_{b_{k+1}}^{b_k},{\mathbf{b}}_a,{\mathbf{b}}_g,{\mathbf{g}}^{b_k}\right]$$所谓“以机器人中心定义状态变量”指的就是参与迭代扩展卡尔曼滤波是${\mathbf{x}}_{b_{k+1}}^{b_k}$，而${\mathbf{x}}_w^{b_k}$是根据${\mathbf{x}}_{b_{k+1}}^{b_k}$的滤波结果进行更新，本身不参与滤波，而${\mathbf{x}}_{b_{k+1}}^{b_k}$指的是在$k+1$帧坐标系下第$k$帧的位姿，因此可以避免线性化过程误差的累计。
${\mathbf{x}}_{b_{k+1}}^{b_k}$的误差状态变量定义如下$$\mathbf{\delta }\mathbf{x}:=\left[\mathbf{\delta }\mathbf{p},\delta \mathbf{v},\delta \theta ,\delta {\mathbf{b}}_a,\delta {\mathbf{b}}_g,\delta \mathbf{g}\right]$$误差状态$\delta \mathbf{x}$、标称状态${}^{-}{\mathbf{x}}_{b_{k+1}}^{b_k}$与真实状态${\mathbf{x}}_{b_{k+1}}^{b_k}$关系如下$${\mathbf{x}}_{b_{k+1}}^{b_k}=-{\mathbf{x}}_{b_{k+1}}^{b_k}\text{ 田 }\mathbf{\delta }\mathbf{x}=\left[\begin{array}{c}-{\mathbf{p}}_{b_{k+1}}^{b_k}+\delta \mathbf{p}\\ -{\mathbf{v}}_{b_{k+1}}^{b_k}+\mathbf{\delta }\mathbf{v}\\ -{\mathbf{q}}_{b_{k+1}}^{b_k}\otimes \exp (\mathbf{\delta }\theta )\\ {}_a^{-\mathbf{b}}+\mathbf{\delta }{\mathbf{b}}_a\\ -{\mathbf{b}}_g+\mathbf{\delta }{\mathbf{b}}_g\\ -{\mathbf{g}}^{b_k}+\mathbf{\delta }\mathbf{g}\end{array}\right]$$误差状态的i线性连续时间运动模型如下：$$\delta \dot{\mathbf{x}}(t)={\mathbf{F}}_t\delta \mathbf{x}(t)+{\mathbf{G}}_t\mathbf{w}$$其中噪声项$\mathbf{w}={\left[{\mathbf{n}}_a^T,{\mathbf{n}}_g^T,{\mathbf{n}}_{b_a}^T,{\mathbf{n}}_{b_g}^T\right]}^T$，系数矩阵分别为：$${\mathbf{F}}_t=\left[\begin{array}{cccccc}0& \mathbf{I}& 0& 0& 0& 0\\ 0& 0& -{\mathbf{R}}_t^{b_k}{\left[{\hat{\mathbf{a}}}_t\right]}_{\times }& -{\mathbf{R}}_t^{b_k}& 0& 0\\ 0& 0& -{\left[{\hat{\omega }}_t\right]}_{\times }& 0& -{\mathbf{I}}_3& -{\mathbf{I}}_3\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right]$$$${\mathbf{G}}_t=\left[\begin{array}{cccc}0& 0& 0& 0\\ -{\mathbf{R}}_t^{b_k}& 0& 0& 0\\ 0& -{\mathbf{I}}_3& 0& 0\\ 0& 0& {\mathbf{I}}_3& 0\\ 0& 0& 0& {\mathbf{I}}_3\\ 0& 0& 0& 0\end{array}\right]$$其中${\hat{\mathbf{a}}}_t={\mathbf{a}}_{m_t}-{\mathbf{b}}_a$，${\hat{\omega }}_t={\omega }_{m_t}-{\mathbf{b}}_g$，接下来是对运动模型进行离散化，如下：$$\delta {\mathbf{x}}_{t\tau }=\left(\mathbf{I}+{\mathbf{F}}_{t_{\tau }}\Delta t\right)\delta {\mathbf{x}}_{t_{\tau -1}}$$状态变量方差递推如下：$${\mathbf{P}}_{t_{\tau }}=\left(\mathbf{I}+{\mathbf{F}}_{t_{\tau }}\Delta t\right){\mathbf{P}}_{t_{\tau -1}}{\left(\mathbf{I}+{\mathbf{F}}_{t_{\tau }}\Delta t\right)}^T+\left({\mathbf{G}}_{t\tau }\Delta t\right)\mathbf{Q}{\left({\mathbf{G}}_{t_{\tau }}\Delta t\right)}^T$$其中$\Delta t=t_{\tau }-t_{\tau -1}$，而$t_{\tau }$和$t_{\tau -1}$分别是IMU的连续两个时刻，$\mathbf{Q}$是噪声$\mathbf{w}$的矩阵表达。
在此基础上就可以对状态变量进行卡尔曼更新，在卡尔曼迭代滤波中，状态更新类似于优化问题，需要考虑构建一个残差，然后类似于优化一样在每一次迭代中取得不同的更新量，在LIOM中，设计的优化残差为$$\underset{\delta \mathbf{x}}{\min }\Vert \delta \mathbf{x}{\Vert }_{{\left({\mathbf{P}}_k\right)}^{-1}}+\Vert f\left({}^{-}{\mathbf{x}}_{b_{k+1}}^{b_k}\text{ 田 }\mathbf{\delta }\mathbf{x}\right){\Vert }_{{\left({\mathbf{J}}_k{\mathbf{M}}_{\mathbf{k}}{\mathbf{J}}_k^T\right)}^{-1}}$$其中$\Vert \cdot \Vert$为$M$范数，${\mathbf{J}}_k$为函数$f(\cdot )$相对测量噪声的的雅克比，而${\mathbf{M}}_k$为测量噪声矩阵，函数$f(\cdot )$为$$f_i\left({\mathbf{x}}_{b_{k+1}}^{b_k}\right)=\{\begin{array}{cl}\frac{\left|\left({\hat{\mathbf{p}}}_i^{l_k}-{\mathbf{p}}_a^{l_k}\right)\times \left({\hat{\mathbf{p}}}_i^{l_k}-{\mathbf{p}}_b^{I_k}\right)\right|}{\left|{\mathbf{p}}_a^{l_k}-{\mathbf{p}}_b^{l_k}\right|}& \text{ if }{\mathbf{p}}_i^{l_{k+1}}\in {\mathbb{F}}_e\\ \frac{\left|{\left({\hat{\mathbf{p}}}_i^k-{\mathbf{p}}_a^l\right)}^T\left(\left({\mathbf{p}}_a^k-{\mathbf{p}}_b^k\right)\times \left({\mathbf{p}}_a^l-{\mathbf{p}}_c^l\right)\right)\right|}{\left|\left({\mathbf{p}}_a^{l_k}-{\mathbf{p}}_b^{l_k}\right)\times \left({\mathbf{p}}_a^{l_k}-{\mathbf{p}}_c^{l_c}\right)\right|}& \text{ if }{\mathbf{p}}_i^{l_{k+1}}\in {\mathbb{F}}_p\end{array}$$其中${\hat{\mathbf{p}}}_i^{l_k}$是${\mathbf{p}}_i^{l_{k+1}}$通过状态变量变换到当前帧的特征点，如下：$${\hat{\mathbf{p}}}_i^{l_k}={\mathbf{R}}_l^{b^T}\left({\mathbf{R}}_{b_{k+1}}^{b_k}\left({\mathbf{R}}_l^b{\mathbf{p}}_i^{l_{k+1}}+{\mathbf{p}}_l^b\right)+{\mathbf{p}}_{b_{k+1}}^{b_k}-{\mathbf{p}}_l^b\right)$$如果熟悉LOAM或者Lego-LOAM算法的同学应该知道，这个就是LOAM或者Lego-LOAM算法中求解位姿构建的点到线和点到面的残差，在此就不再赘述。通过求解残差，我们可以获得迭代更新公式：$${\mathbf{K}}_{k,j}={\mathbf{P}}_k{\mathbf{H}}_{k,j}^T{\left({\mathbf{H}}_{k,j}{\mathbf{P}}_k{\mathbf{H}}_{k,j}^T+{\mathbf{J}}_{k,j}{\mathbf{M}}_k{\mathbf{J}}_{k,j}^T\right)}^{-1}$$$$\Delta {\mathbf{x}}_j={\mathbf{K}}_{k,j}\left({\mathbf{H}}_{k,j}\mathbf{\delta }{\mathbf{x}}_j-f\left({}^{-}{\mathbf{x}}_{b_{k+1}}^{b_k}\text{ 田 }\delta {\mathbf{x}}_j\right)\right)$$$$\delta {\mathbf{x}}_{j+1}=\delta {\mathbf{x}}_j+\Delta {\mathbf{x}}_j$$其中${\mathbf{H}}_{k,j}$为$f(-{\mathbf{x}}_{b_{k+1}}^{b_k}$ 田 $\mathbf{\delta }{\mathbf{x}}_j)$相对$\delta {\mathbf{x}}_j$的雅克比，在每次迭代过程中，算法都会寻找新的匹配边界点和面点，并计算新的${\mathbf{H}}_{k,j}$、${\mathbf{J}}_{k,j}$和${\mathbf{K}}_{k,j}$，当$f\left({\mathbf{x}}_{b_{k+1}}^{b_k}\right)$小于一定阈值或者达到n次迭代后，我们就可以更新状态变量的残差：$${\mathbf{P}}_{k+1}=\left(\mathbf{I}-{\mathbf{K}}_{k,n}{\mathbf{H}}_{k,n}\right){\mathbf{P}}_k{\left(\mathbf{I}-{\mathbf{K}}_{k,n}{\mathbf{H}}_{k,n}\right)}^T+{\mathbf{K}}_{k,n}{\mathbf{M}}_k{\mathbf{K}}_{k,n}^T$$最后，我们初始化下一阶段${\mathbf{x}}_{b_{k+2}}^{b_{k+1}}$为：$$\left[0_3,{\mathbf{v}}_{b_{k+1}}^{b_{k+1}},{\mathbf{q}}_0,{\mathbf{b}}_a,{\mathbf{b}}_g,{\mathbf{g}}^{b_{k+1}}\right]$$其中，${\mathbf{q}}_0$为单位旋转，${\mathbf{v}}_{b_{k+1}}^{b_{k+1}}={\mathbf{R}}_{b_k}^{b_{k+1}}{\mathbf{v}}_{b_{k+1}}^{b_k}$，${\mathbf{g}}^{b_{k+1}}={\mathbf{R}}_{b_k}^{b_{k+1}}{\mathbf{g}}^{b_k}$，当获得${\mathbf{x}}_{b_{k+1}}^{b_k}$后我们就可以跟新$${\mathbf{x}}_w^{b_{k+1}}=\left[\begin{array}{l}{\mathbf{p}}_w^{b_{k+1}}\\ {\mathbf{q}}_w^{b_{k+1}}\end{array}\right]=\left[\begin{array}{c}{\mathbf{R}}_{b_k}^{b_{k+1}}\left({\mathbf{p}}_w^{b_k}-{\mathbf{p}}_{b_{k+1}}^{b_k}\right)\\ {\mathbf{q}}_{b_k}^{b_{k+1}}\otimes {\mathbf{q}}_w^{b_k}\end{array}\right]$$

3.3 实验结果

LINS的实验结果如下：

注意这里的LIOM指的是《Tightly Coupled 3D Lidar Inertial Odometry and Mapping》中提出的基于优化的方法，从上表中可以看出，LINS精度和LIOM是相当的，但是在下表计算时间的对比中，LINS的优势就非常明显。
这里我们可以来简单理一下LIOM、LINS和MSCKF中滤波状态的区别：
三者相同点都是误差状态，都是根据IMU进行运动方程进行预测，根据激光后者视觉观测进行更新，不同点是LIOM是最基本的误差状态扩展卡尔曼滤波，状态变量中直接包括最终要估计的位姿，而LINS在滤波的状态变量中不包括最终要估计的位姿，而是前后帧相对运动结果，在MSCKF中的状态变量中除了IMU当前时刻的位姿还包括历史的相机状态，IMU相关的状态变量方差在预测过程中预测，而相机相关的状态变量的方差在扩增时预测，因此这三者是各有不同的。

4. LIO-SAM

4.1 总体框架

LIO-SAM总体框如下图所示

从图中可以看出来，IMU数据除了用来构建IMU预积分因子之外，还用来进行激光雷达去即便操作，在IMU预积分完成后，在将IMU将里程计作为先验用来获取激光里程计，激光里程计除了进行Scan-to-Map的匹配之外，还构建一个包括激光雷达因子、GPS因子和回环因子的因子图，用来优化地图和激光里程计的结果，优化后的激光里程计的结果再传递回IMU预积分节点，构建IMU预积分因子图，包括激光里程计因子、IMU预分因子和IMU测量Bias的因子，在论文中给出的因子图如下（看起来是一个，实现起来其实是两个）：

因子图中包括IMU预积分因子、激光雷达里程计因子、GPS因子、回环因子。而我们要估计的状态变量为：$$\mathbf{x}={\left[{\mathbf{R}}^{\mathbf{T}},{\mathbf{p}}^{\mathbf{T}},{\mathbf{v}}^{\mathbf{T}},{\mathbf{b}}^{\mathbf{T}}\right]}^{\mathbf{T}}$$整个优化过程是建立在用于增量平滑的Bayers Tree上的，关于因子图基础知识、Bayers Tree、以及LIO-SAM中关于因子图构建的部分代码我都总结在GTSAM Tutorial学习笔记，下面我仅仅对LIO-SAM中各个因子的基本原理进行介绍。

4.2 因子图构建

在LIO-SAM的因子图中一个有四种因子，我们分别介绍
IMU预积分因子：
IMU从时刻$t$积分到$t+\Delta t$的公式为$${\mathbf{v}}_{t+\Delta t}={\mathbf{v}}_t+\mathbf{g}\Delta t+{\mathbf{R}}_t\left({\hat{\mathbf{a}}}_t-{\mathbf{b}}_t^{\mathbf{a}}-{\mathbf{n}}_t^{\mathbf{a}}\right)\Delta t$$$$\begin{array}{rl}{\mathbf{p}}_{t+\Delta t}={\mathbf{p}}_t& +{\mathbf{v}}_t\Delta t+\frac{1}{2}\mathbf{g}\Delta t^2+\frac{1}{2}{\mathbf{R}}_t\left({\hat{\mathbf{a}}}_t-{\mathbf{b}}_t^{\mathbf{a}}-{\mathbf{n}}_t^{\mathbf{a}}\right)\Delta t^2\end{array}$$$${\mathbf{R}}_{t+\Delta t}={\mathbf{R}}_t\exp \left(\left({\hat{\mathbf{\omega }}}_t-{\mathbf{b}}_t^{\mathbf{\omega }}-{\mathbf{n}}_t^{\mathbf{\omega }}\right)\Delta t\right)$$其中$${\hat{\mathbf{\omega }}}_t={\mathbf{\omega }}_t+{\mathbf{b}}_t^{\omega }+{\mathbf{n}}_t^{\omega }$$$${\hat{\mathbf{a}}}_t={\mathbf{R}}_t^{\mathrm{B}\mathrm{W}}\left({\mathbf{a}}_t-\mathbf{g}\right)+{\mathbf{b}}_t^{\mathrm{a}}+{\mathbf{n}}_t^{\mathrm{a}}$$$${\mathbf{R}}_t={\mathbf{R}}_t^{\mathbf{W}\mathbf{B}}={\mathbf{R}}_t^{\mathbf{B}{W}^{\top }}$$其中预积分测量值为：$$\Delta {\mathbf{v}}_{ij}={\mathbf{R}}_i^{\top }\left({\mathbf{v}}_j-{\mathbf{v}}_i-\mathbf{g}\Delta t_{ij}\right)$$$$\Delta {\mathbf{p}}_{ij}={\mathbf{R}}_i^{\top }\left({\mathbf{p}}_j-{\mathbf{p}}_i-{\mathbf{v}}_i\Delta t_{ij}-\frac{1}{2}\mathbf{g}\Delta t_{ij}^2\right)$$$$\Delta {\mathbf{R}}_{ij}={\mathbf{R}}_i^{\top }{\mathbf{R}}_j$$从公式可以看出来，LIO-SAM中定义的预积分和我们在LIOM和VINS-Mono中定义预积分结果都不太一样，因为在LIO-SAM的代码实现中是直接是用GTSAM中自带的预积分类实现的，这个类中具体怎么实现预积分的还有待考证，初次之泰，IMU Bias因子作为除IMU预积分因子之外单独的一部分参与联合优化。

激光里程计因子
激光里程计和LOAM的原理基本一样，但是区别是LIO-SAM中的构建了关键帧，地图也是利用关键中的特征点构建的局部地图$${\mathbf{M}}_i=\left\{{\mathbf{M}}_i^e,{\mathbf{M}}_i^p\right\}$$其中$${\mathbf{M}}_i^e={}^{\prime }{\mathrm{F}}_i^e{\cup }^{\prime }{\mathrm{F}}_{i-1}^e\cup \dots {\cup }^{\prime }{\mathrm{F}}_{i-n}^e$$$${\mathbf{M}}_i^p={}^{\prime }{\mathrm{F}}_i^p{\cup }^{\prime }{\mathrm{F}}_{i-1}^p\cup \dots {\cup }^{\prime }{\mathrm{F}}_{i-n}^p$$然后是利用Scan-to-Map的原理进行计算的

GPS因子
当接收到GPS测量后，我们首先变换它们到笛卡尔坐标系中。当一个新的位姿节点被插入到因子图后，我们关联GPS因子到该位姿节点中去。具体地，我们线性插值GPS的时间戳，得到对应最新位姿节点的GPS位置。

由于在GPS信号一直存在的时候，持续添加GPS因子没有意义。因为漂移很缓慢。所以在实际操作过程中，我们只添加GPS因子当位姿估计协方差矩阵变得很大的时候。

这一部分原理介绍还是很简单的，因为因子图的构建基于GTSAM本来就很简介，LIO-SAM不太一样的地方其实是一种“半紧耦合”是解决方案，先获得IMU里程计和激光雷达里程计，然后通过因子图的方式将两者结合起来，没那么紧的融合方式效果也很好

4.3 实验结果

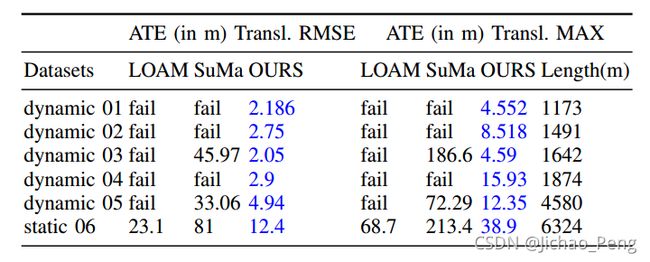
LIO-SAM的实验结果是非常惊艳的，如下图所示：

以及RMSE结果的对比

但是我在别人的博客里看到有同学提到，算法在自己平台上实现效果不是很好，算法我还没有自己跑起来过，之后有时间再测评下。

以上就是所有内容，有问题欢迎交流！

此外，对其他SLAM算法感兴趣的同学可以看考我的博客SLAM算法总结——经典SLAM算法框架总结