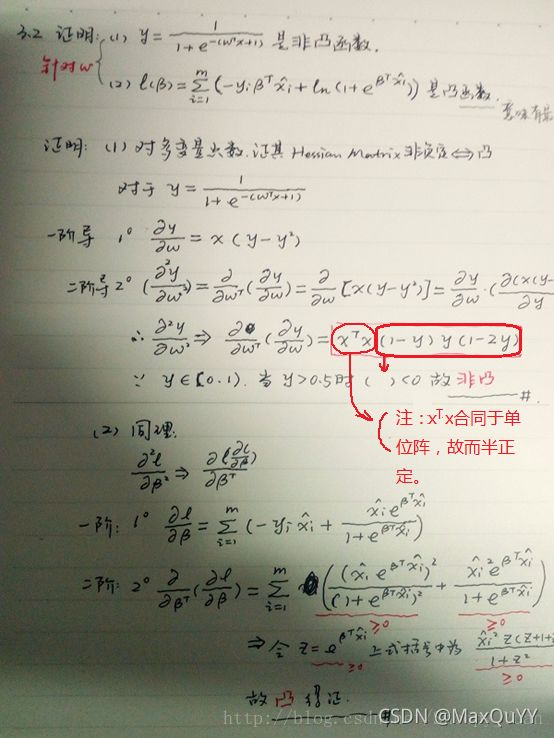【吃瓜教程】周志华机器学习西瓜书第三章答案

线性模型结构梳理

3.1 试析在什么情形下式3.2中不必考虑偏置项b

答案一：

偏置项b在数值上代表了自变量取0时，因变量的取值；

1.当讨论变量x对结果y的影响，不用考虑b；
2.可以用变量归一化（max-min或z-score）来消除偏置。

 答案二：

线性规划的两个实例相减可以消去b，所以 可以令训练集的每一个样本减去第一个样本，然后对新的样本进行线性回归，此时就可不必考虑偏置项。（有点儿类似变量归一化的意思）。 

3.2试证明，对于参数w，对率回归的目标函数是非凸的，但其对数似然函数是凸的（参数存在最优解）。 

凸函数证明方法（充要条件）：若f(x)在D上是半正定的，则f(x)在D上是凸函数。反之不是凸函数。

仅证明了是凸函数， 证目标函数非凸可以证明其海塞矩阵非凸即可。

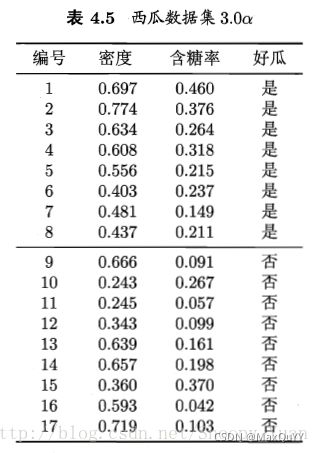
3.3 编程实现对率回归，并给出西瓜数据集3.0a上的结果。 

编程实现对率回归：
思路一：* 采用sklearn逻辑斯蒂回归库函数实现，通过查看混淆矩阵，绘制决策区域来查看模型分类效果（直接调用封装好的对数几率回归函数）；
思路二：* 自己编程实现，从极大化似然函数出发（找损失函数），采用梯度下降法得到最优参数（求解可行最优解），然后尝试了随机梯度下降法（优化参数）来优化过程。

1.获取数据、查看数据、预处理： 

（待更新）

3.4 选择两个UCI数据集，比较十折交叉验证法和留一法所估计存储的对率回归的错误率。

 （待更新）

3.5编程实现线性判别分析（LDA），并给出西瓜数据集3.0a上的结果。

（待更新）

3.6线性判别分析仅在线性可分数据集上能获得理想结果，试设计一个改进方法，使其能较好地用于非线性可分数据。 

在当前维度线性不可分，可以借助适当的映射函数映射到高维空间，使其在高维空间线性可分。（有定理证明:数据在低维线性不可分但经过映射后总会在一个高维空间线性可分，支持向量机处可能有证明）（事实上，这也是分类问题处理线性不可分数据的主要思路）

给出两种思路：

• 参考书p57，采用广义线性模型，如 y-> ln(y)。
• 参考书p137，采用核方法将非线性特征空间隐式映射到线性空间，得到KLDA（核线性判别分析）。

 3.7 令码长为9，类别数为4，试给出海明距离意义下理论最优的ECOC（纠错输出码）二元码并证明。

对于ECOC二元码，当码长为2的n次方时，至少可以使2n个类别达到最优间隔，他们的海明距离为2的n-1次方。

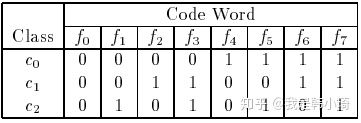
参考书p65，对于同等长度的编码，理论上来说，任意两个类别间的编码距离越远，纠错能力越强。那么如何实现呢，可参考文献Error-Correcting Output Codes。下图是截取文中的关于在较少类时采用exhaustive codes来生成最优ECOC二元码的过程：

机器学习（周志华）课后习题——第三章——线性模型 - 知乎 (zhihu.com)

原书对很多地方解释没有解释清楚，把原论文看了一下《Solving Multiclass Learning Problems via Error-Correcting Output Codes》。

先把几个涉及到的理论解释一下。

首先原书中提到：

对同等长度的编码，理论上来说，任意两个类别之间的编码距离越远，则纠错能力越强。因此，在码长较小时可根据这个原则计算出理论最优编码。

其实这一点在论文中也提到，“假设任意两个类别之间最小的海明距离为 d ，那么此纠错输出码最少能矫正   位的错误。

拿上图论文中的例子解释一下，上图中，所有类别之间的海明距离都为4，假设一个样本正确的类别为c1 ，那么codeword应该为 ‘0 0 1 1 0 0 1 1’，若此时有一个分类器输出错误，变成‘0 0 0 1 0 0 1 1’，那么此时距离最近的仍然为 c1 ，若有两个分类输出错误如‘0 0 0 0 0 0 1 1’，此时与   的海明距离都为2，无法正确分类。即任意一个分类器将样本分类错误，最终结果依然正确，但如果有两个以上的分类器错误，结果就不一定正确了。这是   的由来。

第一点其实就是原书提到的，已经解释过了，说说第二点：

如果两个分类器的编码类似或者完全一致，很多算法（比如C4.5）会有相同或者类似的错误分类，如果这种同时发生的错误过多，会导致纠错输出码失效。（翻译原论文）

个人理解就是：若增加两个类似的编码，那么当误分类时，就从原来的1变成3，导致与真实类别的codeword海明距离增长。极端情况，假设增加两个相同的编码，此时任意两个类别之间最小的海明距离不会变化依然为 d ，而纠错输出码输出的codeword与真实类别的codeword的海明距离激增（从1变成3）。所以如果有过多同时发出的错误分类，会导致纠错输出码失效。

另外，两个分类器的编码也不应该互为反码，因为很多算法（比如C4.5，逻辑回归）对待0-1分类其实是对称的，即将0-1类互换，最终训练出的模型是一样的。也就是说两个编码互为补码的分类器是会同时犯错的。同样也会导致纠错输出码失效。

当然当类别较少时，很难满足上面这些条件。如上图中，一共有三类，那么只有 2的3次方=8 中可能的分类器编码（   ），其中后四种（   ）是前四种的反码，都应去除，再去掉全为0的 ，就只剩下三种编码选择了，所以很难满足上述的条件。事实上，对于  种类别的分类，再去除反码和全是0或者1的编码后，就剩下  中可行的编码。

原论文中给出了构造编码的几种方法。其中一个是：

回到题目上，在类别为4时，其可行的编码有7种，按照上述方法有：

当码长为9时，那么 f6 之后加任意两个编码，即为最优编码，因为此时再加任意的编码都是先有编码的反码，此时，类别之间最小的海明距离都为4，不会再增加。

类别数为4，因此1V3有四种分法，2V2有六种分法，3V1同样有四种分法。按照书上的话，理论上任意两个类别之间的距离越远，则纠错能力越强。那么可以等同于让各个类别之间的累积距离最大。对于1个2V2分类器，4个类别的海明距离累积为4；对于3V1与1V3分类器，海明距离均为3，因此认为2V2的效果更好。因此我给出的码长为9，类别数为4的最优EOOC二元码由6个2V2分类器和3个3v1或1v3分类器构成。

另一种答案

纠错输出码原理及文献综述

 3.8 ECOC编码能起到理想纠错作用的重要条件是：在每一位编码上出错的概率相当且独立。试分析多分类任务经ECOC编码后产生的二分类器满足该条件的可能性及由此产生的影响。

 ECOC编码能起到理想纠错作用的重要条件是：在每一位编码上出错的概率相当且独立。因为一个码位的出错率较高，会导致这个码位的保持相同的较低信用，进而不再具有分类作用。这就相当于全0或全1的分类器，这点和NFL定理（没有免费的午餐定理）前提很像。但由于样本很难满足每一位编码出错的概率相当且独立，所以书中提到了有多种问题依赖的ECOC问题

 3.9 使用OvR和MvM将多分类任务分解为二分类任务求解时，试述为何无需专门针对类别不平衡性进行处理。

参考书p66，对OvR、MvM来说，由于对每类进行了相同的处理，其拆解出的二分类任务中类别不平衡的影响会相互抵销，因此通常不需专门处理。

以OvR（一对其余）为例，由于其每次以一个类为正其余为反（参考书p63），共训练出N个分类器，在这一过程中，类别不平衡由O的遍历而抵消掉。

以ECOC编码为例，每个生成的二分类器会将所有样本分成较为均衡的二类，使类别的不平衡性的影响减小。当然拆解后仍然可能出现明显的类别不平衡现象，比如一个超级大类和一群小类。

 3.10试推导出多分类代价敏感学习（仅考虑基于类别的误分类代价）使用“再缩放”能获得理论最优解的条件。

见 周志华《机器学习》课后习题（第三章）：线性模型_红色石头的专栏-CSDN博客

参考：周志华《机器学习》课后习题解答系列（四）：Ch3 - 线性模型_Snoopy_Yuan技术部落格-CSDN博客

西瓜书机器学习课后答案周志华.pdf-原创力文档 (book118.com)